Анализ результатов автоматизированной проверки знаний для определения объективности составленных тестирований

Автоматизация процессов обучения и контроля знаний является одним из ключевых направлений развития современной образовательной системы. В условиях постоянно растущего объема информации и необходимости ее оперативного освоения традиционные методы оценки знаний сталкиваются с рядом ограничений. Это обусловливает актуальность поиска и разработки новых, более эффективных методов и инструментов для проверки и оценки знаний.

Одним из перспективных направлений в этой области является создание и использование автоматизированных систем для проведения тестирования. Автоматизированные тесты позволяют не только существенно сократить время на проверку знаний, но и повысить объективность оценок. Однако возникает вопрос о соответствии результатов, полученных с помощью автоматизированных систем, традиционным методам оценки, а также о влиянии этих методов на процесс обучения в целом.

Подходы к анализу эффективности проверки знаний

Анализ эффективности автоматизированной проверки знаний, основанный на сравнении ее результатов с традиционными экзаменами, позволяет оценить ее точность и на

Анализ результатов автоматизированной проверки знаний для определения ...

Никитина Галина Михайловна аспирант, ассистент кафедры прикладной математики и искусственного интеллекта, Национальный исследовательский университет «МЭИ», Москва. Сфера научных интересов: разработка программного обеспечения, информационные системы.

дежность. Такой подход помогает определить, насколько автоматизированные тесты могут заменить традиционную оценку и усовершенствовать процесс оценивания знаний.

Визуальный анализ взаимосвязи результатов тестирования и традиционной проверки знаний важен для оценки точности и объективности оценок. Использование графиков и диаграмм помогает визуализировать эту связь, облегчая понимание сложных данных, выявление тенденций и аномалий. Этот анализ способствует обнаружению выбросов, которые могут искажать результаты, и их последующему исключению или объяснению. Кроме того, визуальный анализ полезен для исследования распределения оценок, позволяя определить, например, слишком легкие или сложные методы тестирования.

Пример гистограммы представлен на Рисунке 1. В легенде справа показаны оценки тестирования, а по горизонтальной оси – экзаменационные оценки.

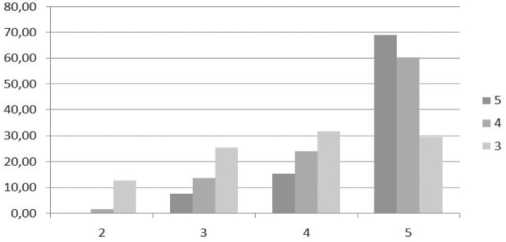
Рисунок 1. Гистограмма частот экзаменационных оценок Источник: [1].

По гистограмме делаются следующие выводы:

• ≈ 70 % студентов, сдавших тест на оценку «5», на экзамене получили оценку «5»;

• •    ~ 84 % студентов, сдавших тест на оценку «5», на экзамене получили оценку «4» или «5»;

• •    ~ 84 % студентов, сдавших тест на оценку «4», на экзамене получили оценку «4» или «5»;

• •    ~ 87 % студентов, сдавших тест на оценку «3», на экзамене получили положительную оценку.

Кроме визуального анализа важную роль играет регрессионный анализ , представляющий собой составление уравнения парной линейной регрессии, а также оценку параметров этого уравнения.

Рассмотрено предположение о линейной зависимости экзаменационных оценок y от результатов тестирования x с помощью модели линейной регрессии y = mx + b + e . В этой модели m и b считаются детерминированными, а показатель e – случайной величиной с нормальным распределением и нулевым математическим ожиданием [2].

Уравнение регрессии всегда дополняется показателем тесноты связи. Полученный при расчетах коэффициент корреляции будет показывать тесноту связи; чем ближе коэффициент корреляции к 1, тем теснее связь двух оценок, полученных различными способами проверки знаний.

Примеры тесной и слабой связи оценок приведены на Рисунке 2.

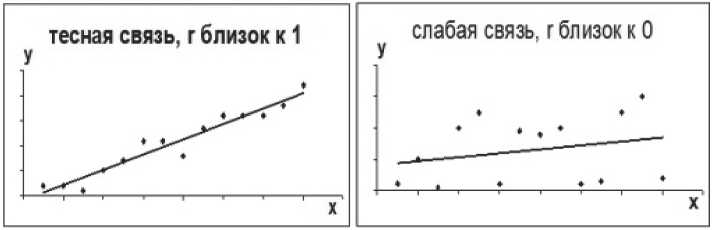
Рисунок 2. Примеры тесной и слабой связи Источник: [3].

Для проверки значимости линейной зависимости оценок используется критерий Фишера (F).

Для определения критерия Фишера необходимо сопоставить факторную и остаточную дисперсии в расчете на одну степень свободы:

F _ ^D фaкm Docm

F-статистика используется для проверки гипотезы H ₀ : если эта гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга; если гипотеза не справедлива, то факторная дисперсия больше остаточной дисперсии в несколько раз.

Табличное значение критерия F – это максимальная возможная величина отношения дисперсий при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы.

Если вычисленное значение F-отношения больше табличного, то это отношение признается достоверным. В этом случае гипотеза об отсутствии связи признаков отклоняется. Следовательно, связь существует. Когда значение F оказывается меньше табличного, то ги-

Анализ результатов автоматизированной проверки знаний для определения ...

потеза не может быть отклонена без риска сделать неверный вывод о существовании связи. Но уравнение регрессии в таком случае будет считаться статистически незначимым [4].

Введение латентной переменной y ^* , связанной с оценкой тестирования x почти линейной зависимостью

*

y = mx + b + e ,                                      (2)

позволяет учесть дискретность оценок. Пороговые значения μ соответствуют различным экзаменационным оценкам k. Модель может быть логит- (логистическое распределение возмущения) или пробит-моделью (нормальное распределение возмущения). Основная задача – определение параметров модели, обычно через метод максимального правдоподобия. Оценка тестиро- вания и соответствующие вероятности получения разных экзаменационных оценок позволяют оценить соответствие между результатами тестирования и экзаменационными оценками [4].

Анализируя зависимость результатов экзамена и результатов тестирования, можно сделать вывод, что регрессионная модель не совсем удобна для использования из-за дис- кретности переменных, которые искажают результат, поэтому следует произвести анализ с помощью модели множественного выбора, а для визуализации данных использовать визуальный и регрессионный анализ.

В этой модели для учета дискретности оценок вводится латентная переменная y*, варьирующаяся от 0 до 100. Переменная μ определяет пороговые значения для разных экзаменационных оценок. Используя логистическое распределение для возмущений и метод максимального правдоподобия, рассчитываются вероятности различных экзаменационных оценок в зависимости от результатов тестирования. Эти расчеты помогают понять соответствие между оценками тестирования и экзамена и учитывают ограничения, например, увеличение экзаменационной оценки при повышении результатов теста:

*

2, У i ,

У* =1

*

3, H i ^ y

< H 2 ,

*

4, H 2 ^ У

< ^Н з ,

После получения оценок параметров модели надо вычислить вероятности получения различных оценок на экзамене (2, 3, 4, 5) для каждой из оценок тестирования. Оценка «2» тестирования не рассматривается, так как студент, получивший эту оценку, к экзамену не допускается [5].

Исходя из описанных методов, формулируется методика анализа результатов автоматизированной проверки знаний:

Для анализа результатов тестирования и экзаменов сначала собираются и обрабатываются данные из систем дистанционного обучения и оценок, исключая студентов, отсутствующих на тестах или экзаменах. После этого строятся гистограммы результатов, чтобы определить, есть ли корреляция между оценками тестов и экзаменов. Если наблюдается зависимость, проводится регрессионный анализ: рассчитываются коэффициенты корреляции и детерминации, а также проверяется значимость уравнения регрессии с помощью критерия Фишера. Эти шаги помогают оценить силу и важность связи между оценками. При подтверждении связи необходимо применить логит-модель для вычисления вероятностей различных оценок на экзамене, основываясь на результатах тестов, и определить параметр β с использованием метода максимального правдоподобия.

Весь анализ предназначен для определения наличия статистически значимой связи между оценками, полученными студентами в тестах и на экзаменах, что важно для оценки эффективности методов тестирования и их соответствия традиционным экзаменационным оценкам.

Реализация основных функций прототипа приложения

При проектировании приложения использован паттерн MVC (Model-ViewController), разделяющий приложение на три основные группы компонентов: Модели, Представления и Контроллеры [6].

В рамках проекта библиотека Chart.js также используется для проведения регрессионного анализа, включая построение корреляционных полей с линиями регрессии. Ключевые коэффициенты для анализа вычисляются непосредственно в контроллере приложения. Наглядный пример такого расчета коэффициентов линейной регрессии выглядит следующим образом:

string [] xxData = column2Data.ToArray();

double covariance = 0;

double variance = 0;

double ySumOfSquares = 0;

double yResidualsSumOfSquares = 0;

Length - 1);

Дополнительно в процессе разработки была проведена оценка значимости полученного уравнения линейной регрессии:

Важной частью реализации прототипа является применение метода максимального правдоподобия. Для этого был разработан алгоритм расчета функции правдоподобия, который является ключевым элементом в применении данного метода:

var data = new Tuple, List>(table, column2Data, column3Data);

excelTableModel.paramsS = 27.5;

double var1 = excelTableModel.paramsB;//b double var2 = excelTableModel.paramsS;//s double var3 = excelTableModel.paramsM;//m double Ln(double b, double s, double m){ double likelihoodTerm = 0.0;

Анализ результатов автоматизированной проверки знаний для определения ...

expTerm)));

}

} return likelihoodTerm;

}

Анализ результатов работы

Получившееся приложение полностью адаптировано для пользователя. Оно включает в себя все необходимые для анализа инструменты.

При запуске приложения пользователь попадает на главную страницу (Рисунок 3), где необходимо загрузить заранее подготовленный файл с результатами автоматизированного тестирования и результатами традиционного экзамена. При необходимости существует возможность изменения процентных границ для оценок.

Анализ результатов автоматизированной проверки знаний

Добро пожаловать!

Данное приложение разработано для упрощения анализа результатов автоматизированной проверки знаний с использованием метода множественного выбора с упорядоченными альтернативами.

Для начала работы необходимо загрузить подготовленный файл и ввести ваши процентные границы оценок. Затем нажать кнопку "Загрузить".

Далее Вы увидите полный анализ результатов автоматизированной проверки знаний, который включает в себя:

• 1.    Визуальный анализ;

• 2.    Регрессионный анализ;

• 3.    Анализ данных с испол ьзованием модели множественного выбора.

| | выберите файд | Файл не выбран

Оценка "4" за тест ставится с 175

Оценка "5“ за тест ставится с |б5

Рисунок 3. Главная страница приложения

Источник: рисунки 3–9 являются авторскими.

После загрузки файла пользователь видит итог полного анализа результатов автоматизированной проверки знаний.

Сначала отображаются исходные данные (см. Рисунок 4).

Затем осуществляется визуальный анализ с помощью гистограммы (см. Рисунок 5) и регрессионный анализ, включающий в себя поле корреляции с линией тренда (см. Рисунок 6), параметры линейной регрессии и оценку значимости уравнения линейной регрессии (см. Рисунок 7).

Далее применяется метод максимального правдоподобия с упорядоченными альтернативами, включающий в себя исходные и измененные параметры функции правдоподо- бия, натуральные логарифмы вероятностей получения оценок (необходимо для сравнения с другими средами) и вероятности получения оценок (см. Рисунок 8).

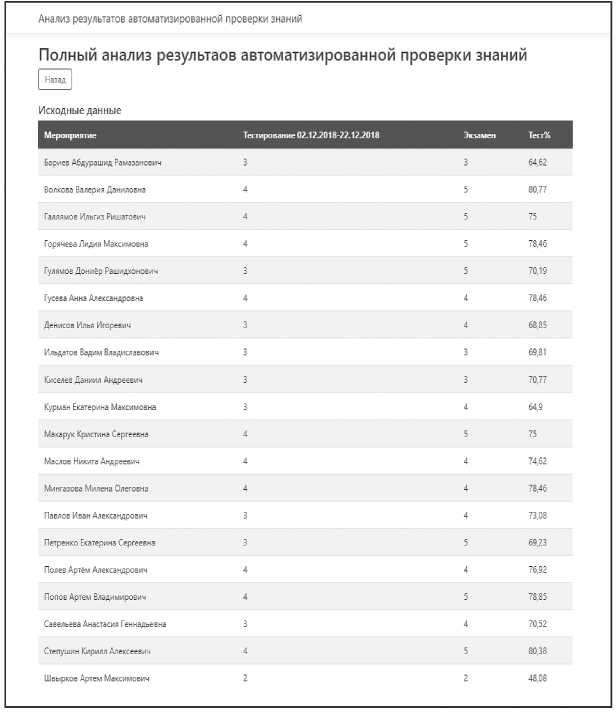
Рисунок 4. Исходные данные

Анализ результатов автоматизированной проверки знаний для определения ...

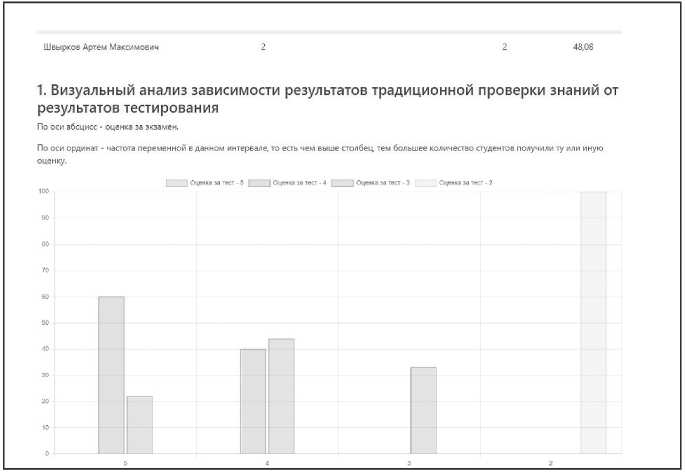
Рисунок 5. Визуальный анализ

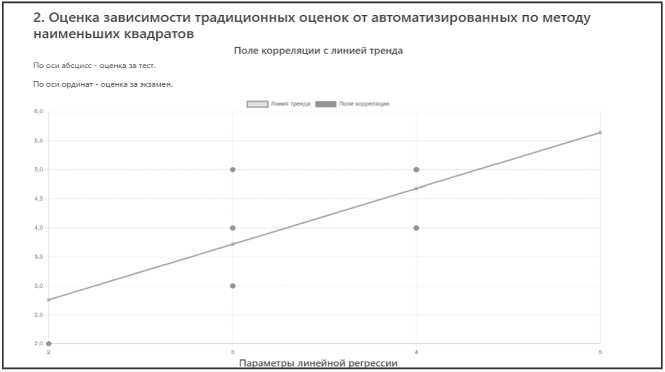
Рисунок 6. Поле корреляции с линией тренда

Рисунок 7. Параметры линейной регрессии и оценка значимости уравнения регрессии

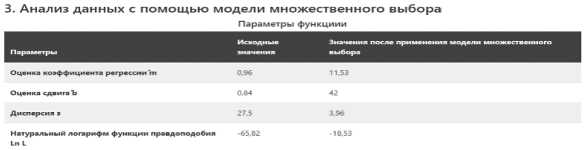
Натуральные логарифмы вероятностей (необходимо для сравнения с другими статистическими средами)

Вероятности получения различных оценок за экзамен в зависимости от оценки за тестирование

Рисунок 8. Модель множественного выбора

Проанализировав все результаты, пользователь видит исходную таблицу, в которую добавлен еще один столбец со значениями латентной переменной (см. Рисунок 9).

Анализ результатов автоматизированной проверки знаний для определения ...

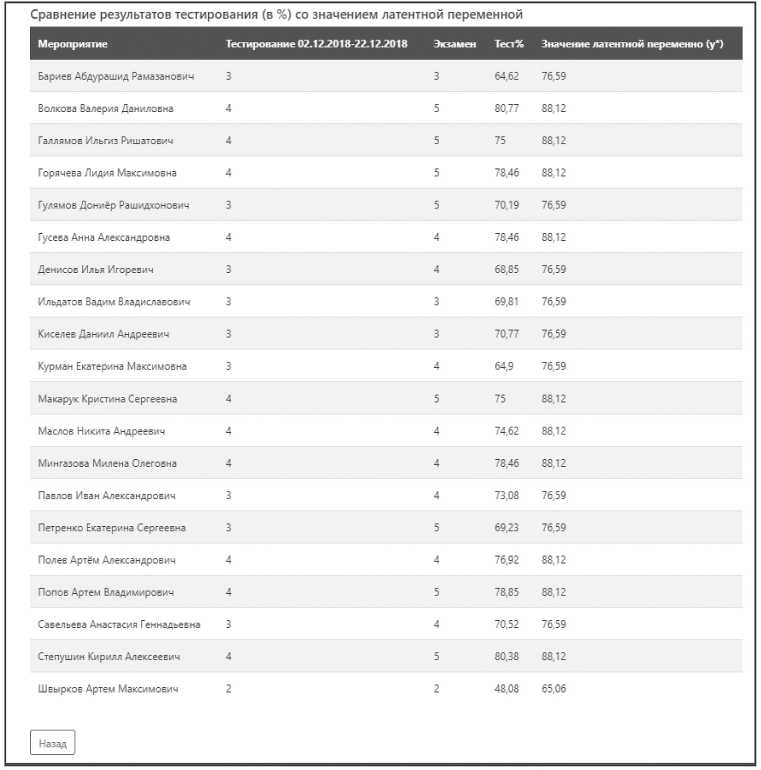
Рисунок 9. Сравнение результатов тестирования со значением латентной переменной

Именно на основании показателей латентной переменной делается вывод, что преподаватель оценивает эффективнее, чем СДО «Прометей», так как оценки, поставленные преподавателем на экзамене, более точно попадают в границы латентной переменной.

Заключение

Таким образом, разработка и применение методики анализа результатов автоматизированной проверки знаний и соответствующего веб-приложения показывают значительный потенциал для оптимизации образовательного процесса. Использование упорядоченных альтернатив в тестах множественного выбора позволяет достичь более высокого уровня точности и объективности в оценке знаний.

Использование таких систем позволяет точнее и объективнее оценивать знания студентов, упрощает процесс обучения и снижает риск человеческих ошибок при оценке. Это также способствует индивидуализации обучения и оптимизации учебных методов, делая образование более адаптивным и справедливым.