Анализ результатов математического моделирования процесса нанесения микроуглублений на поверхность коллектора

Проблема повышения износостойкости поверхностей трения обычно решается созданием дискретного микрорельефа, который удерживает смазку в рабочей зоне контактирующих поверхностей. [1-10]. Недостатками этих способов является низкая производительность и получение гладких впадин дискретного микрорельефа, которые плохо удерживают смазку.

Нетривиальным решением проблемы повышения износостойкости коллекторной пары электродвигателей является нанесение на поверхность коллектора микроуглублений накаткой шлифовальной лентой [11-13]. Необычность данного процесса состоит в том, что он приводит к многократному повышению износостойкости коллектора. Чтобы понять и обосновать возможность применения процесса нанесения микроуглублений шлифовальной лентой, автор на основе ранее выполненных исследования в области теории абразивной обработки [14, 15], теории деформирования тонких оболочек [16] и закономерностей теории вероятностей построил математическую модель этого процесса [13] и показал высокую его эффективность. Было установлено, что эффективность процесса формирования на поверхности коллектора микроуглублений обеспечивается тем, что в процессе работы электродвигателя частички износа графитовых щеток запрессовываются в микроуглубления и начинают играть роль твердой смазки. Ниже приведен анализ результатов математического моделирования процесса формирования микроуглублений прокаткой шлифовальной ленты. процесса.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

В результате прокатки шлифовальной ленты на поверхности коллектора формируются микроуглубления со случайными геометрическими параметрами. Суммарная площадь всех микроуглублений на обрабатываемой поверхности зависит как от числа этих микроуглублений, так и от их размеров, которые являются случайными величинами. Известно, что математическое ожидание произведения случайных величин равно произведению математических ожиданий этих величин:

^S»= ^Zo' ^S_O’                                     (1)

где S_o – математическое ожидание суммарной площади всех микроуглублений, мм ² , z_o – среднее число микроуглублений на поверхности коллектора; s_o – средняя площадь микроуглублений, мм ² .

Величины s и z являются независимыми случайными величинами, так как величина z зависит от диаметра абразивных зерен, а величина s от диаметра зерен не зависит. Следовательно, дисперсия

суммарной площади микроуглублений определяется по известной в теории вероятностей зависимости, как дисперсия произведения двух независимых случайных величин:

0(5) = D(s) • 0(z) + 0(s) • z² + D(z) • s²,                     (2)

где ОД – дисперсия числа микроуглублений на единице поверхности, равная для закона Пуассона D(Z) = Zo; 0 (J) – дисперсия распределения площади микроуглублений, равная ад = ^ .

Если накатка микроуглублений осуществляется не за один оборот заготовки, то надо учесть, что при последующих проходах часть микроуглублений попадет в предыдущие микроуглубления. Например, если осуществляется второй проход, то вероятность этого события будет равна:

P = S’—,(3)

F где   – площадь ранее накатанных микроуглублений,    ; – площадь поверхности, на которую накатываются микроуглубления,    ; – площадь вновь накатываемых микроуглублений,.

С учетом (3) площадь, занимаемая микроуглублениями после повторного прохода, будет равна:

S2 = \ + (5 -5yJ,(4)

Но так как второй проход осуществляется тем же инструментом при тех же условиях, что и первый, то следует принять 5 = 5j. Тогда равенство (4) примет вид:

52 =5X- (2 -y),(5)

Аналогично (5) определим площадь микроуглублений, оставленных на обрабатываемой поверхности после третьего прохода:

/       5,\       /   5. S² \

^3  ^2 + ^1  ^1 p J 3^1 p + 2p2 ) '

Подобно (6) определим суммарную площадь микроуглублений после к -ого прохода:

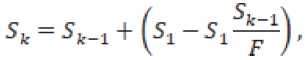
где S к – суммарная площадь микроуглублений после К -ого прохода, лш ; ^ t“l – суммарная площадь микроуглублений после (Ai -1)-ого прохода, VW .

По той же методике находим и число микроуглублений, оставленных абразивными зернами после к -ого прохода:

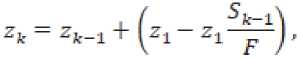
Как видно, зависимости (7) и (8) носят рекуррентный характер.

На основе полученных математических моделей разработан алгоритм и протестирована на языке программирования MatCad система компьютерного имитационного моделирования процесса формирования микроуглублений на поверхности коллекторов электродвигателей накаткой шлифовальной лентой, и выполнен компьютерного эксперимента, который выявил и наглядно представил зависимости вероятностных параметров микроуглублений на поверхности коллектора от зернистости абразивного инструмента и числа проходов шлифовальной ленты.

На рис. 1 и 2 представлены зависимости среднего значения площади впадины от зерен и их среднего числа на обрабатываемой поверхности.

Как видно из рисунков 1 и 2, с увеличением зернистости инструмента площадь единичных впадин от зерен увеличивается, а число впадин уменьшается. Это объясняется тем, что более крупные абразивные зерна могут оставить более глубокие канавки большей площади, чем мелкие зерна. Но крупнозернистый инструмент имеет меньшее удельное число зерен, чем мелкозернистый, поэтому и число оставленных этими зернами углублений получается меньшим.

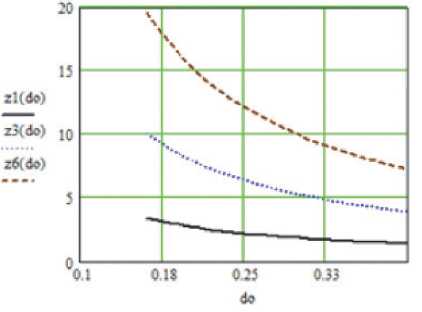
На рис. 3 представлена зависимость среднего значения суммарной площади впадин от зерен и числа впадин на единице поверхности коллектора в зависимости от зернистости инструмента.

Как видно из рисунка 3, с увеличением зернистости площадь впадин от зерен возрастает, а число микровпадин от зерен уменьшается. Объясняется это тем, что с возрастанием зернистости увеличивается возможная глубина впадин от зерен. А так как площадь впадины имеет квадратичную зависимость от ее глубины, то с возрастанием зернистости увеличиваются площади впадин. Число

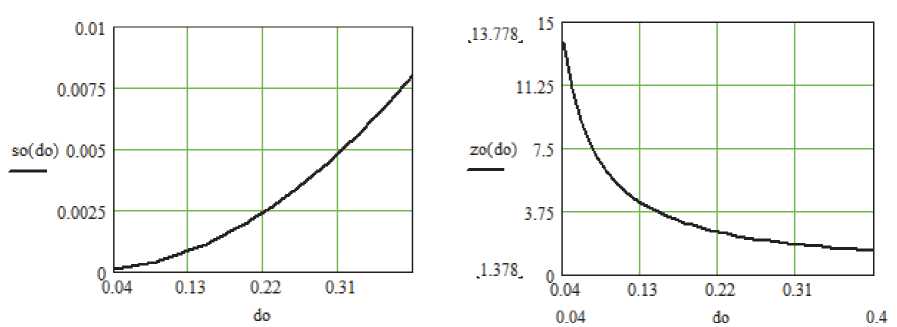
Рис. 1. Зависимость средней площади впадины от зерен s ₀ от зернистости инструмента d ₀

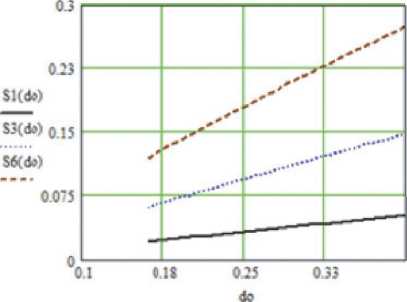
Рис. 2. Зависимость среднего числа впадин от зерен z ₀ от зернистости инструмента d ₀

зерен в меньшей степени зависят от зернистости. Поэтому в целом зависимость носит возрастающий характер.

С увеличение числа проходов при накатке микровпадин суммарная их площадь и число возрастает. Так как площадь микровпадин намного меньше площади, на которую они наносятся, то степень перекрытия их при повторных накатках незначительно, а влияние этого фактора на суммарную площадь впадин невелико.

Таким образом, предложенная математическая модель позволяет выявить закономерности влияния зернистости шлифовальной ленты на площадь микроуглублений и их числа, оставленными абразивными зернами при прокатке коллектора шлифовальной лентой.

ЗАКЛЮЧЕНИЕ

Выполненный анализ выявил зависимость суммарной площади микроуглублений и их числа, оставленными абразивными зернами при прокатеке коллектора электродвигателя шлифовальной лентой, от зернистости инструмента. Установлено, что с увеличением зернистости шлифовальной ленты число микроуглублений на единице поверхности коллектора уменьшается, а суммарная площадь микроуглублений возрастает. Объясняется это тем, что с возрастанием зернистости уменьшается число абразивных зерен на единице поверхности инструмента, но увеличивается их глубина внедрения в обрабатываемую поверхность. А так как площадь впадины имеет квадратичную зависимость от ее глубины, то в целом зависимость доли микроуглублений на поверхности коллектора носит возрастающий характер.