Анализ рисков деятельности экономических субъектов

Автор: Курбанмагомедова К.З., Эрик А.А., Хазиахметова А.Р.

Журнал: Экономика и бизнес: теория и практика @economyandbusiness

Статья в выпуске: 5-2 (87), 2022 года.

Бесплатный доступ

Функционирование экономических субъектов в рыночной экономике предполагает их деятельность в условиях постоянно действующих и многообразных рисков, в силу чего анализ и оценка этих рисков является крайне важных и всегда актуальным видом деятельности любого хозяйствующего субъекта. Математический инструментарий - один из самых эффективных методов оценки рисков. В статье рассмотрен пример принятия решений инвестором об инвестировании в ряд отраслей экономики России по ряду критериев (критерии Лапласа, максимакса, Вальда, Гурвица, Севиджа) и показан алгоритм принятия решения, который обеспечивает наилучшее решение в условиях неопределенности и риска.

Еще

Риски деятельности, критерии выбора в условиях риска, критерий лапласа, критерий вальда, критерий гурвица, критерий севиджа

Короткий адрес: https://sciup.org/170192413

IDR: 170192413

Текст научной статьи Анализ рисков деятельности экономических субъектов

Тема рисков в деятельности экономических субъектов настолько обширная, что нет смысла в рамках данной статьи описывать все виды рисков, их факторы, методы и способы борьбы (управления) с ними.

Поэтому целесообразно «заузить» понятие «анализ рисков деятельности экономических субъектов» до понятия «анализ рисков при принятии решения о выборе направлений деятельности». И в целях данного исследования под риском деятельности экономических субъектов будем понимать «риск, связанный с выбором направления предпринимательской деятельности» [1, с. 31], Особенность его в том, что в момент принятия управленческих решений относительно выбора направления деятельности практически невозможно получить точные и полные знания об отдаленной во времени среде, в которой будет осуществляться деятельность организации, обо всех действующих или потенциально возможных внешних и внутренних факторах, оказывающих на нее влияние. А выбор сделать надо. В этих условиях (впрочем, под эти условия можно «подогнать» и любые условия хозяйствен-

ной деятельности) крайне важно сделать правильный выбор. В большинстве случаев управлением риска «занимается» математика (за исключением случаев, когда решения принимаются интуитивно или интуитивными методами) [3].

Приведем пример с условным инвестором, но реальными данными по экономике России, который принимает решение об инвестировании в ту или иную отрасль.

Данный инвестор имеет интерес инвестировать в 3 отрасли:

- строительство (стратегия А1);
- производство строительных материалов (стратегия А2);
- или просто положить деньги на депозит (стратегия А3).

Уровень доходности, который получит инвестор, зависит от экономического состояния в России, которое имеет 3 состояния:

- экономический рост (состояние С1);
- стагнация (состояние С2);
- экономический кризис (состояние С3).

Размеры возможной доходности отражены в таблице 1.

Таблица 1. Матрица последствий (размеры доходности инвестиций в зависимости от состояния экономики)

Стратегия	Матрица последствий
Стратегия	С1	С2	С3
А1	24	15	2
А2	18	15	8
А3	6	8	10
max	24	15	10

	A	В	С	D
1		Матрица последствий
2		Cl	С2	СЗ
3	Al	24	15	2
4	A2	18	15	8
5	A3	6	8	10
6	max	24	15	10
7
8		Матрица рисков
9		Cl	С2	СЗ
10	Al	0	0	8
11	A2	6	0	2
12	A3	18	7	0

Рис. 1. Матрица последствий и матрица рисков

В условиях неопределенности суще- Принципы расчета этих критериев от- ствует несколько критериев выбора: ражены в таблице 2.

Лапласа; максимакса; Вальда; Гурвица;

Севиджа [2, с. 166].

Таблица 2. Принципы расчета критериев риска [2, с. 102]

Критерии	Суть критерия	Формула расчета
Лапласа	В основе этого критерия лежит "принцип недостаточного основания": если нет достаточных оснований считать, что вероятности того или иного спроса имеют неравномерное распределение, то они принимаются одинаковыми и задача сводится к поиску варианта, дающего	fl" S = max — ) ISS-I n 1
Максимакс	По этому критерию определяется вариант решения, максимизирующий максимальные выигрыши для каждого варианта ситуации. Это критерий крайнего («розового») оптимизма, в соответствии с которым наилучшим является решение, дающее максимальный выигрыш, равный max(max q _ij). Рассматривая i-е решение, предполагают самую хорошую ситуацию, приносящую доход а _i = max q _ij , а затем выбирают решение с наибольшим значением a _i .	S = max a _i = max(min q _i j ).
Вальда (правило максимина, или критерий крайнего пессимизма)	Рассматривая i-е решение, будем полагать, что на самом деле ситуация складывается наихудшая, то есть приносящая наименьший доход a _i = min q _i j . Но теперь выберем решение i ₀ с наибольшим a _i0 .	S = max a _i = max(min q _i j ).
Гурвица (взвешивающий пессимистический и оптимистический подходы к выбору решений)	По данному критерию выбирают вариант решения, при котором достигается максимум выражения сi = α min qij+ (1 - α) max qij , где α выражает долю пессимизма (параметр пессимизма) в характере ЛПР, причем α€[0; 1]. Таким образом, критерий Гурвица рекомендует руководствоваться некоторым средним результатом между крайним оптимизмом и крайним пессимизмом. При α=0 критерий Гурвица совпадает с критерием максимакса, а при α=1 с критерием Вальда. Значение α выбирается из субъективных (интуитивных) соображений	с_i = α min q_i j + (1 - α) max q_i j
Севиджа	Этот критерий аналогичен критерию Вальда, но ЛПР принимает решение, руководствуясь не матрицей последствий Q={q_i j }, а матрицей рисков R= {r_i j }. По этому критерию наилучшим является решение, при котором максимальное значение риска будет наименьшим, то есть равным min(max r_i j ). Рассматривая i-е решение, предполагают ситуацию максимального риска ri = max r_i j и выбирают вариант решения i₀ с наименьшим r_i0	R = min r _i = min (max r ij )

Приведем расчет для нашего условного инвестора:

	A	в	с	D	E	F	G	H	I J
1		Матрица последствий			критерий Лапласа		критерий Вальд	критерий Гурвица
2		Cl	C2	C3	ср.знач.	max	min	a = 0,5
3	Al	24	15	2	19,5	24	2	13,0
4	A2	18	15	8	16,5	18	8	13,0
5	A3	6	8	10	7,0	10	6	8,0
6	max	24	15	10	19,5	24	8	13,0

Рис. 2. Выбор стратегии инвестирования по критерию Лапласа

Очевидно, что максимальное среднее значение – 19,5%, значит, наилучшая стратегия по критерию Лапласа – это А1 (инвестирование в строительную организацию).

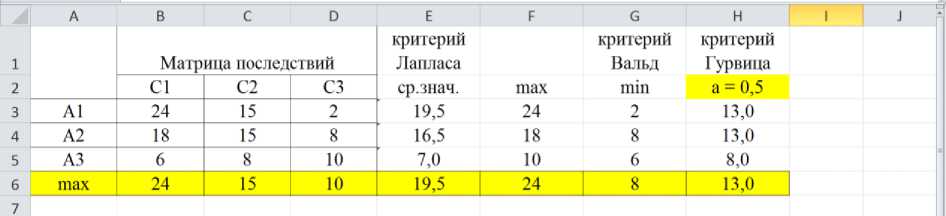
Рис. 3. Выбор стратегии инвестирования по критерию максимакса

Очевидно, что максимальное значение – 24%, значит, наилучшая стратегия по критерию максимаска – это А1 (инвестирование в строительную организацию).

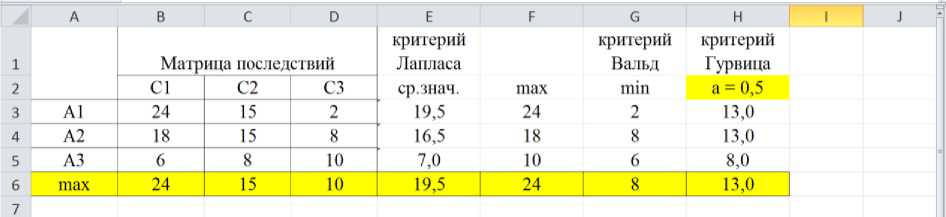
Рис. 4. Выбор стратегии инвестирования по критерию Вальда

Очевидно, что максимальное из мини- А2 (инвестирование в компанию по произ-мальных значений – 8%, значит, наилуч- водству строительных материалов).

шая стратегия по критерию Вальда – это

	А	в	с	D	Е	F	G	н
1		Матрица последствий			критерий Лапласа		критерий Вальд	критерий Гурвица
2		С1	С2	СЗ	ср.знач.	max	min	а = 0,4
3	А1	24	15	2	19,5	24	2	15,2
4	А2	18	15	8	16,5	18	8	14,0
5	АЗ	6	8	10	7,0	10	6	8,4
6	max	24	15	10	19,5	24	1 8	15,2 \|

Рис. 5. Выбор стратегии инвестирования по критерию Гурвица

Очевидно, что оптимальным решением по критерию Гурвица (при a = 0,4) – это А1 (инвестирование в строительную организацию).

А	А	В	с	D	Е	F
1		Матрица последствий			критерий Лапласа
2		С1	С2	СЗ	ср.знач.	max
3	А1	24	15	2	19,5	24
4	А2	18	15	8	16,5	18
5	АЗ	6	8	10	7,0	10
6	шах	24	15	10	19,5	24
7
8		Матрица рисков			критерий Севиджа
9		С1	С2	СЗ	шах
10	А1	0	0	8	8
11	А2	6	0	2	6
12	АЗ	18	7	0	18

13 6 = мин

Рис. 6. Выбор стратегии инвестирования по критерию Сэвиджа

Очевидно, что минимальным из максимальных значений риска будет значение 6%, значит, наилучшая стратегия по критерию Севиджа – это А2 (инвестирование

в компанию по производству строительных материалов).

Обобщим результаты расчетов в таблице 3.

Таблица 3. Расчетные значения критериев выбора стратегии

Критерий	Выбор
Лапласа	А1 (инвестирование в строительную организацию)
Максимакса	А1 (инвестирование в строительную организацию)
Вальда	А1 (инвестирование в строительную организацию)
Гурвица	А2 (инвестирование в компанию по производству строительных материалов)
Севиджа	А2 (инвестирование в компанию по производству строительных материалов)

Список литературы Анализ рисков деятельности экономических субъектов

Смирнов В.Д., Колокольчиков А.В. Теория игр в жизни и бизнесе // Вестник науки и образования. - 2020. - №12 (90) - С. 30-32.
Хаим Шапира. Гладиаторы, пираты и игры на доверии. Как нами правят теория игр, стратегия и вероятности. - М.: Азбука-Аттикус. - 2021. - 140 с.
Бакирова, Р.Р. Внешние риски предпринимательской деятельности хлебопекарной промышленности / Р.Р. Бакирова, Э.Ф. Сагадеева, В.О. Скорнякова // Региональные проблемы преобразования экономики. - 2022. - №1 (135). - С. 52-59. - DOI 10.26726/1812-7096-2022-1-52-59. - EDN YHMOEP.
Бакирова Р.Р. Методы оценки и управления рисками на предприятиях / Р.Р. Бакирова, А.А. Бадретдинова, Э.Ф. Сагадеева // Российский электронный научный журнал. - 2017. - №1 (23). - С. 83-94. - EDN YKVBTJ.
Бакирова Р.Р. Статистические методы оценки структурных сдвигов в динамике // Кооперация в науке и инновациях: Материалы Международной научно-практической конференции профессорско-преподавательского состава, сотрудников, докторантов и аспирантов вузов по итогам работы за 2014 год, Ярославль-Москва, 19 февраля 2015 года / Автономная некоммерческая образовательная организация высшего образования "Российский университет кооперации". - Ярославль-Москва: Издательство "Канцлер", 2015. - С. 52-56. - EDN UAWYAN.
Оценка рисков инвестиционных проектов Республики Башкортостан / Т.В. Наконечная, Ф.С. Растегаева, Т.В. Баронина [и др.]. - Уфа: государственное автономное учреждение дополнительного профессионального образования Институт развития образования Республики Башкортостан, 2019. - 64 с. - ISBN 978-5-7159-0753-0. - EDN FHDDRT.

Еще

Статья научная