Анализ силового взаимодействия литой детали с формой

Решение задачи о силовом взаимодействии литой детали с формой невозможно без определения деформаций, возникающих в данной системе. При рассмотрении литой осе-симмеричной детали с плоскими поверхностями элементов затруднения усадки (рис. 1) для определения напряжений в стенке отливки проведем разбиение сжимаемой среды на ряд слоев xi. Ввиду воздействия теплового потока отливки, каждый слой будет отличаться жесткостью, выражаемой произведением модуля Юнга Ei на площадь сжимаемого слоя Ai. Таким образом, в первом приближении нахождение деформации системы под воздействием усадочных процессов можно осуществить путем решения статически неопределимой задачи о центральном сжатии элементов различной жесткости. Решение данной задачи в условиях упругих деформаций позволяет найти абсолютное перемещение z плоскости 1 в положение 1/ (см. рис.1.), при изменении температуры стенки отливки z =

Е отл А отл 1 2^ 2 - 1 1 )

Е отл А отл 1 2 + 2^ EA

; npui = 1,..., n

где E отл A отл – жесткость стенки отливки; ℓ 2 , ℓ 1 – расстояния между плоскостями, затрудняющих усадку элементов, до изменения температуры и после изменения температуры в условиях сводной усадки сплава.

Cиницкий Евгений Валерьевич, кандидат технических наук, доцент кафедры электрометаллургии и литейного производства. E-ma l: e-v-s@ma l.ru

Тубольцева Алена Сергеевна, старший преподаватель кафедры теоретической механики и сопротивления материалов.E-ma l: a-tus@ma l.ru

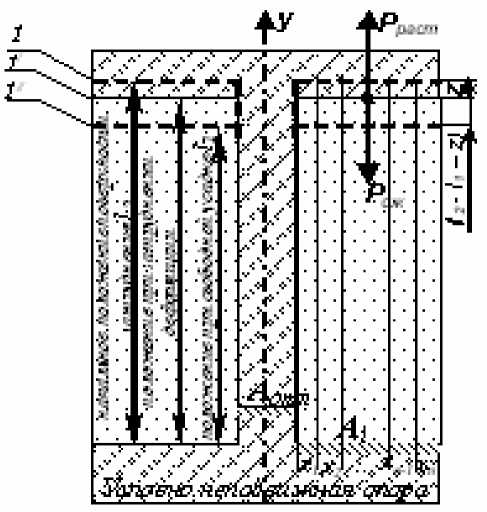
Рис. 1. Схема к расчету деформации системы «отливка-форма» при затрудненной усадке

Плоскости 1 (см. рис.1) отображают начальное положение системы, 1^/ - положение после изменения температуры стенки отливки A T, 1 ^м - положение при допущении о свободной усадке материала. Значение ℓ 1 не трудно найти как

1 1 = 1 ₂ -A Т а 1 ₂,              (2)

где а - коэффициент линейного расширения сплава.

Ранее проведенные исследования [1] по расширению базы данных сопротивления деформации сырых и сухих формовочных смесей в различных температурных условиях позволяют получить значения модулей Юнга Ei, используемых в уравнении (1). В ходе эксперимента варьировали содержание связующего (каолиновых и бентонитовых глин) в пределах 010%, начальной влажности 0-10%, плотности 1350-1750 т/м3, температур 20-900оС. Осевое сжатие исследуемых образцов обеспечивали путем их нагружения в устройстве (рис. 2). На основе полученных данных были разработаны нейросетевые модели, прогнозирующие относительную деформацию смесей £ (рис. 3):

£ — f (P; р0; U0; T;%),                (3)

где Р - усилие нагружения; р₀, U 0 - начальные плотность и влажность образца; T - температура смеси; % - компонентный состав образца.

Полученные модели показали высокую сходимость расчетных и экспериментальных данных (корреляционное отношение для сырых смесей п_с ыр =0,96, сухих п_сух=0,98).

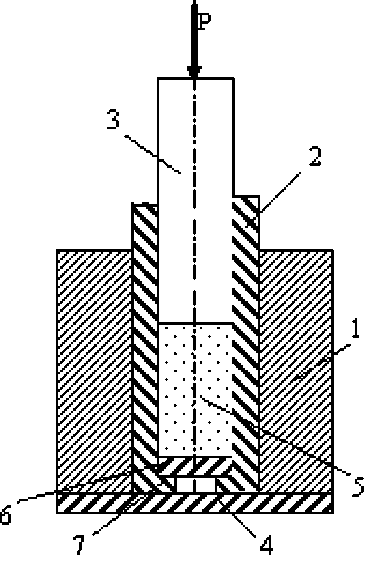
Рис. 2. Установка для определения податливости формовочной смеси:

1 - корпус; 2 - обойма; 3 - шток; 4 - опора; 5 - образец; 6 - шайба; 7 - ограничитель

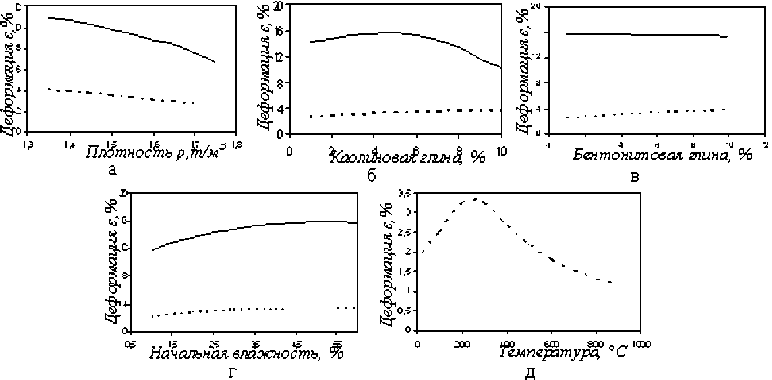
Рис. 3. Расчетные зависимости влияния на деформацию формовочной смеси:

a - плотности; б - содержания каолиновой глины; в - содержания бентонитовой глины; г - начальной влажности; д - температуры; прямая линия - сырая смесь, пунктир - сухая смесь

Как показано в работе [1], значительное влияние на деформационную способность формообразующей среды оказывает температура слоя. Учитывая, что при моделировании деформации системы производили разбивку сжимаемой среды на ряд слоев xi, то для нахождения ее температуры, изменяемой под воздействием теплового поля отливки, удобно использовать явную разностную схему [2], по которой, температура каждого слоя в текущий момент времени описывается следующими уравнениями:

T- ^{+ 1} = fT k + (1 - 2 f ) T * + fT k + 1 , i — 1,..., n - 1;

Т n ^{+ 1} = 2 fT_n ^k - 1 + [ 1 - 2 f ( 1 + b )№ + 2 fbT₀

при f

XA t   ,L

, b —, c3KАх2

экв где Тiк+1, Тiк – температура i-го слоя в текущий и предыдущий момент времени соответственно; Т0 – температура окружающей среды; λ – теплопроводность смеси; Δt – временной отрезок в промежутке между к-м и к+1 моментом времени; Δx – величина i-го интервала системы; сэкв – объемная теплоемкость слоя смеси; L – коэффициент теплоотдачи.

Устойчивость решения при применении выражений (4), (5) обеспечивается выполнением следующего условия f <  ^j - b ) •

Для учета влияния на температурное поле избыточной, химически несвязанной влаги слоя формы в уравнениях (4), (5) использовали следующее выражение эквивалентной теплоемкости с экв [3]:

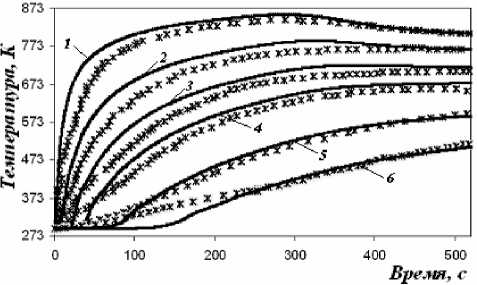
Рис. 4. Температурные кривые сырой песчаноглинистой формы: прямая линия – расчетные; ж – экспериментальные значения; 1 – 2,5 мм от границы металл-форма; 2 – 5 мм; 3 – 7,5 мм; 4 – 10 мм; 5 – 15 мм; 6 – 20 мм

С экв = ( 57,15 + 11,06 - T "10 -3 ) ^0⁰⁰ р + К х

М SiO

(               0,672 2,87 - 10 — 3 U 2 + 29,42810 — 2 U ₀ - 1.849

х | 1 - th^{U 0}   e

T к — T c

(

2(9,653 - 0,023 U 0 ln( U 0 ) - 1,2511ln( U 0 ))

) | x

_X___________ 6180ф_о ___________

9,653 - 0,023 U , ln( U 0 ) - 1,2511ln( U 0 ) ,

2 <  U 0 < 14,

где M SiO2 – молярная масса оксида кремния; ρ сух – плотность высохшего слоя формы; К – поправочный коэффициент, К=0,98.

Применение выражения (6) в уравнениях (4), (5) позволило с достаточной точностью учесть влияние влаги формы на динамику нагрева слоя. Что подтвердилось при сравнении экспериментальных данных источника [4] с расчетными кривыми (рис. 4).

Одним из основополагающих факторов, влияющих на деформацию системы «отливка-форма», являются геометрические параметры зон испарения и конденсации слоя формовочной смеси. Анализ экспериментальных данных по влиянию на геометрию зоны конденсации начальных параметров формы, приведенных в работах [5, 6], позволил разработать физикоаналитическую модель расчета формирования зоны конденсации [7]. По предложенным алгоритмам создана программа расчета кривых конденсации, прогнозирующая распределение влажности в слое сырой песчано-глинистой формы [8]. Экспериментальная проверка работы программы детально описана в источнике [7]. Программа позволяет производить расчет кривой конденсации с начальной влажностью формы U 0 = 2-14%, начальной плотностью формы ρ 0 = 1400-1660 кг/м³ (рис. 5).

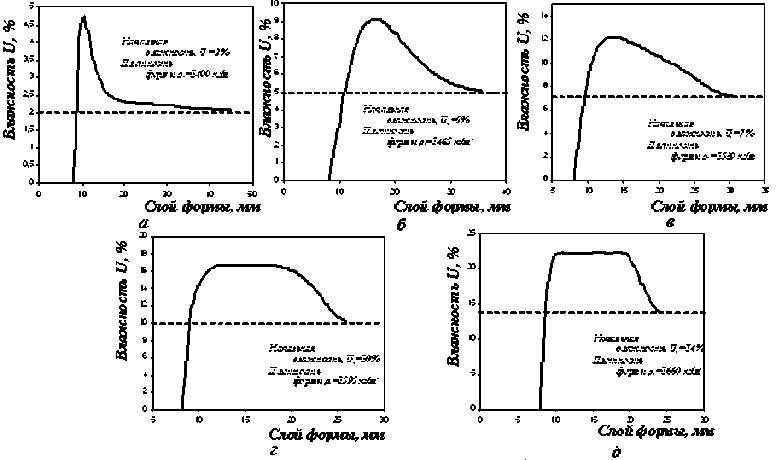
Рис. 5. Кривые распространения влажности в слое формовочной смеси при различных начальной влажности U 0 и плотности ρ 0 формы: а – U 0 =2%, ρ 0 =1400 кг/м³; б – U 0 = 5%, ρ 0 =1465 кг/м³; в – U 0 =7%, ρ 0 =1530 кг/м³; г – U 0 =10%, ρ 0 =1595 кг/м³; д – U 0 =14%, ρ 0 =1660 кг/м³

Выводы: проведенная работа позволяет моделировать основные граничные условия формирования линейного напряженного состояния литой детали в процессе ее охлаждения при рассмотрении осесимметричных элементов затруднения усадки с параллельными плоскостями внедрения.