Анализ системы амортизации инерциального прибора как решение задачи многокритериальной оптимизации

В филиале АО «ЦЭНКИ» - «НИИ ИМ им. академика В. И. Кузнецова» (НИИ ИМ) проводится разработка бесплатформенного измерительного прибора космического назначения (прибор). Особенностью этого прибора является предъявление требований к повышенной точности измерений при его работе в составе космического аппарата (КА) [1], одновременно с требованиями к повышенной вибростойкости при движении ракеты-носителя, в том

числе в нештатных режимах ее полета [2]. Прибор является важной подсистемой бесплат-форменной инерциальной навигационной системы (БИНС) [3], в которой определяются координаты объекта как результат решения навигационной задачи [4] по данным из аксе-лерометрических (АК) и гироскопических (ГК) измерительных каналов.

Для выполнения целевой задачи в АК прибора применены прецизионные вибрационнострунные акселерометры (ВСА) [5], а в ГК - волоконно-оптические гироскопы (ВОГ) [6] собственной разработки НИИ ИМ. ВСА обладают высокой чувствительностью и широким диапазоном измерения полезного линейного ускорения [7, 8] благодаря применению струны из определенного материала с сечением, вносящим минимальные искажения в показания АК. Но вместе с этим струна крайне чувствительна и к вредным перегрузкам. Для обеспечения виброзащиты ВСА реализована внутренняя система амортизации и демпфирования (САД) [9], которая обеспечивает защиту струны при штатных режимах полета [10], но при нештатных ее недостаточно, и, предположительно, возникают удары [11] подвижных элементов [12] о корпус ВСА с закономерным разрывом струны. Для исключения этого процесса требуется применение дополнительной САД [13,14].

Поэтому первичной задачей при разработке прибора стало обеспечение вибростойкости ВСА [15,16]. Но, поскольку прибор является основным компонентом БИНС КА, важным становится и обеспечение вибростойкости алгоритма определения координат в целом [17, 18]. Кроме того, на прибор накладываются и иные ограничения, связанные с технологическими возможностями его изготовления в НИИ ИМ и его конструктивными особенностями, существенными при монтаже в КА. Вследствие вышеизложенного целью настоящей работы является поиск наиболее эффективного исполнения САД с использованием методов многокритериальной оптимизации [19].

2.    Описание модели

Принципиальная конструкция САД включает в себя блок чувствительных элементов (БЧЭ), на котором жестко установлены ВСА. БЧЭ связан с корпусом прибора через равножесткие пружины. Для гашения собственных колебаний БЧЭ применяются виброгасящие демпферы (ВД) и демпферы сухого трения. ВСА сам по себе также является колебательной системой. Рассматриваемая конструкция САД приведена ниже (рис. 1).

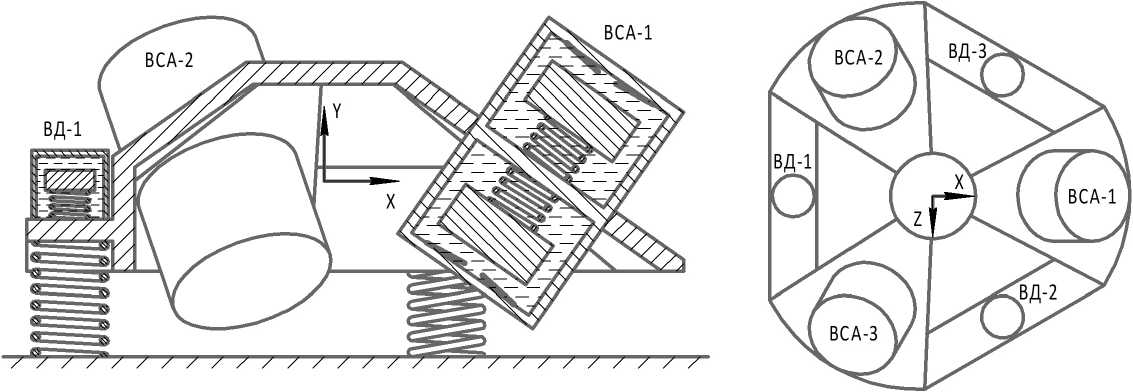
Рис. 1. Схема моделируемой конструкции САД

Такое исполнение с математической точки зрения имеет вид многомассовой колебательной системы. Движение подвижных элементов конструкции описывается следующей нелинейной системой дифференциальных уравнений [20]:

Мл ^х R r ^{— —} Й^ + й ( ^F fi)

3 ∑︀ i=1

3 ∑︀ i=1

3 ∑︀ i=1

3 ∑︀ i=1

(P bi + Р иг ) ^{х R}Rbi ^{— Н} Ь ^{х R} bi ^{— R}k^ ^ + (рЫ ^х ( ^R bi ^{— (H} b ^{— Е} ) ^{х R} bi ^{— R} k )) ^—

(наг

¹ х (G ai + C_ui) х H_ai х (iCi — (Н ь — Е ) х -Й — Й))

(G di х (-Й - (H b - Е ) ц( - Й) ) = ^Й

—

M ai ^{х H} ai ^х ^Ra— ^— Й^ ^{+ (P} ai ^{+ P} ui ) ^{х H} ai ^х ( Ra — ^{— Н} b ^{х R} ai ^— R b^ + (G ai + G ui] х H ai х ( R ai — (H b — Е ) х R ^ — д) = ^Й ,i = 1 , 2 , 3

M_d i х

G di х

RR di ^— Й^ + ^p di ^х RR(H ^{— H} b ^{х R} di ^{— R}b^ ’ (iCi — (H b — Е ) х R di — R b) = Й ,i = 1 , 2 , 3

—

+

„       3

J b ^х Z b + й (Rfi ^{х F} fi} + i=1 ^x            '

,

3 ∑︀ i=1

3 ∑︀ i=1

3 ∑︀ i=1

3 ∑︀ i=1

RR bi х (P bi + P ы) х k

(Rbi х G bi х (Rbi

(Rai ^{х H}ai

—

—

^H b ^{х R} bi ^{— R} in^ ^ +

(H b — Е ) х R bi — R k))

¹ х (G_ai + G_u) х H_ai lab         u fat

(^Rdi ^{х G}di ^х (Ди

—

—

^х (Rai ^{— (H} b ^{— Е}) ^{х R} ai ^{— R} b )) ^—

(H b — Е ) х Ri — R bi) ) = Й

JJ b + M b х R fi) Д P /—a —a\ й ( (^Rbi ^— R fj) ,й № — Rfj) e (( R k — R fj) e (( R di— R fj)

хй + й (( R fi i=1 ^{V V}

^— R fj)

^х R fi) +

й  ТД  —k х (pbi + pui] х ( R—   Hb х Rbi

—Й)

+

х

х

^G bi ^х (Rbi ^{— (H} b ^{— Е ) х R} bi ^{— R} k ))

—

H a-¹ х (G ai + G ui) х H ai х (дЬ — (H b — Е ) х Д* — Rb) )

х G di х ( R di — (H b — Е ) х R di — R bi)) = ^C ,j = 1 .. 3

где к, b, a, u,d, v, f ~ элементы конструкции: корпус, БЧЭ, ВС А, контактные демпферы в ВСА, ВД, дополнительные вязкое и сухое трение соответственно; М, P, G, J ~ масса,вязкость, жесткость, момент инерции элемента; ё, ё, е - угловые ускорение, скорость и поворот БЧЭ; H,H матрица поворота элемента и ее производная, определяемые из ё, е; Е - единичная матрица; R,R,R - линейные ускорение, скорость и перемещение элемента; i - номер элемента: j - номер элемента, силы трепня: Ff - сила, трепня: g - ускорение свободного падения.

Для поиска решений в несколько этапов [21-23] разработана нелинейная матмодель на Python, в которой система уравнений решается посредством дискретного интегрирова- ния [24] с использованием метода «LSODA» в функции scipy.integrate.solve_ivp. В качестве входных данных модели применяются параметры, связанные с конструкционными характеристиками САД БЧЭ и ВД (масса, частота, добротность) и однозначно идентифицирующие экземпляр САД для последующего анализа.

В приборе, как компоненте БИНС КА требуется измерение абсолютного перемещения в неподвижной системе координат. Поэтому необходимо осуществить преобразование относительных линейных координат, измеряемых в АК, с применением абсолютных угловых координат в ГК [25]. Возможны несколько вариантов размещения АК и ГК: на БЧЭ, подвижном относительно корпуса прибора, или напрямую на самом корпусе. При использовании иных вибростойких акселерометров возможно их закрепление на корпусе прибора. Выбор места установки ГК связан в том числе с наличием его чувствительности к линейному ускорению. В настоящей работе принимается, что ВОГ как оптоэлектронное устройство [26] малочувствителен к линейному ускорению и его показания зависят только от угловых колебаний. В настоящей работе, как и в реальном приборе принимается, что ГК жестко связан с корпусом прибора, а АК расположен на БЧЭ (рис. 2).

Ж

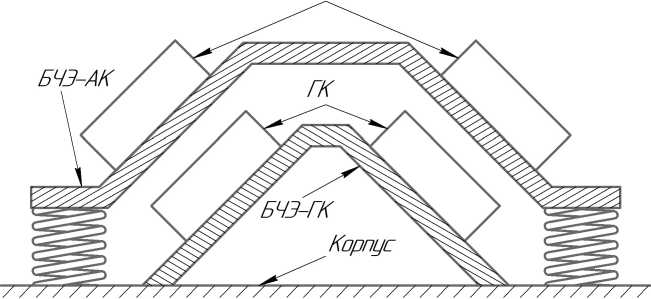
Рис. 2. Текущее исполнение САД АК и ГК БИНС

При подобной компоновке чувствительных элементов возникает противоречие при разработке САД - необходимо уменьшить как опасное относительное перемещение в ВСА, так и погрешность решения целевой задачи в БИНС. Исходя из особенностей эксплуатации прибора, в том числе требований к минимальным габаритным размерам при использовании в составе КА, важным является поиск исполнения САД с минимальным относительным перемещением БЧЭ и минимальной массой БЧЭ и ВД.

3.    Решение задачи напрямую

Для поиска оптимального исполнения САД [27] были введены нормированные базовые критерии, описывающие погрешность измерения координат ( М) - ошибку построения траектории, уязвимость (F) - запас перемещения до появления касания в ВСА, габариты (S) - массу и геометрические размеры БИНС, сложность изготовления ( D) - то насколько в НИИ ИМ сложно изготовить прибор с заданными характеристиками:

/       \²     (              / г" \².

^F  ml^y У³^^ ⁺ ^УХа^) ⁺ V^ax^ ’

М =

^ Х +Ф 2 +^ 2 3 · 9

- 4;

S =

M_b +3 - M _d - 0,6 2Д,3

+

^r X2 + ^r y² + ^{r b} 2

4 • 3 •r

b max

D =

33A-1 । 3^d Wb  ⁺ 10 ’

где г^, г™, г™ - проекции перемещения подвижной массы г-го ВС А относительно его корпуса на его характерные оси X, Y, Z соответственно; х^_ах, У^^ z^ax ^_ предельные перемещения по соответствующим осям ВС А, при которых происходят его касания о корпус; гХч Гу, г? - проекции перемещения подвижной массы БЧЭ относительно корпуса прибора на его характерные оси X, Y, Z соответственно; г\_ах - предельное перемещение вдоль любой оси БЧЭ, при котором происходит касание о корпус прибора; а_х, а_у, a_z - CKO при измерении соответствующих координат траектории движения КА.

Наилучшим значением любого приведённого критерия является 0, а наихудшим - 1. Таким образом, поиск наилучшего исполнения САД с математической точки зрения является задачей минимизации. За первичную область поиска был принят технически допустимый диапазон отклонений конструктивных характеристик САД от номинальных значений, реализованных в реальном приборе. Было проведено итерационное моделирование с изменением массы, добротности САД и частоты САД БЧЭ и ВД. Масса и добротность входят напрямую в принятые критерии, а частота является косвенным фактором.

В итоге моделирования получены данные для 2300 экземпляров САД. Из них 1730 запусков оказались успешными, т.е. в них не было касания ни в БЧЭ, ни в ВС А. В первую очередь была предпринята попытка решения многокритериальной задачи оптимизации напрямую, при помощи поиска неулучшаемых исполнений методом Парето. В результате моделирования было определено, что единого Парето-фронта для всех критериев не существует, и поэтому невозможно обнаружить гиперплоскость неулучшаемых исполнений. При исключении одного или нескольких критериев можно будет добиться создания области оптимальных решений, но предпочтительно не терять важную информацию о различных исполнениях САД (рис. 3).

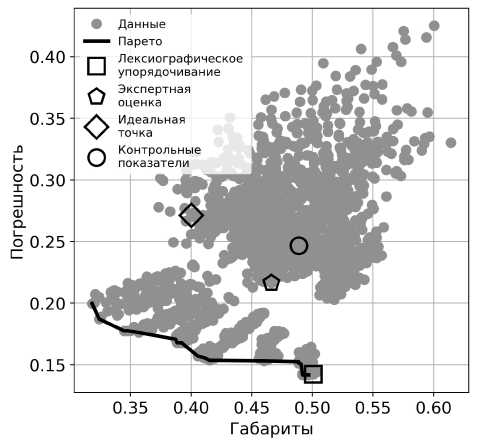
а)

Рис. 3. Примеры Парето-фронтов при исследовании взаимосвязи двух критериев (а - Габариты и

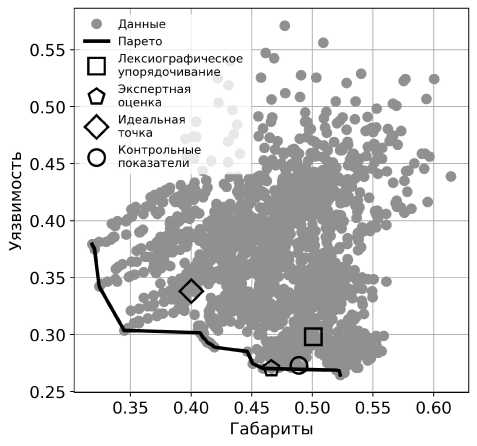
б)

Погрешность, б - Габариты и Уязвимость)

Дополнительно для рассмотренных исполнений был проведен анализ погрешности при различном расположении АК и ГК. Было обнаружено, что различия между вариантами несущественны и для дальнейшего исследования будет приниматься текущий вариант САД, состоящий из ВОГ, размещенного на корпусе прибора, и ВС А размещенного на БЧЭ. Для наглядности результаты были отсортированы по увеличению погрешности при расположении ГК и АК на БЧЭ, с сохранением их относительного расположения в каждой точке. Значения по оси X вследствие их неинформативности не приводятся (рис. 4).

4.    Сведение задачи к однокритериальной

Поскольку напрямую не удалось обнаружить подходящее исполнение, были введены скалярные критерии оценки эффективности, учитывающие величины базовых критериев. Для удобства последующих работ вначале был введен барьер (Т), определяемый прошедшим модельным временем от старта замера, при котором произошло касание в БЧЭ или в ВС А:

Т = 1000 • (1 - Дд/Дам).

где Дд - модельное время от старта замера при котором произошло первое касание в БЧЭ или в ВСА; Дам - планируемая модельная продолжительность замера.

Были предложены четыре разноплановых критерия, основанных на способах скаля-ризации многокритериальной задачи оптимизации. Причем с целью дальнейшей автоматизации процесса вычисления для всех критериев определяется максимальное значение между вычисленным критерием и барьером. Критерий, вычисленный по методу идеальной точки ( I) подразумевает определение модуля вектора, построенного из желаемой точки к точке пространства критериев, описывающей конкретное желаемое исполнение. Среди всего массива векторов находится наименьший, в рассматриваемом случае это точка ближе всего расположенная к началу координат, в которой все базовые критерии равны 0:

I = max Q0 , 5 • \ М ² + F ² + S ² + D ²] , Т .

Критерий, вычисленный по методу контрольных показателей ( К) основан на поиске наиболее удаленной от критичного значения точки, в рассматриваемой задаче от точки, для которой все базовые критерии равны 1:

К = max (1 - ^0, 5 • ^(1 - М )² + (1 - F)² + (1 - S)² + (1 - D )²j , Т^ .

Среди экспертов был проведен опрос о приоритетности расположения базовых критериев по их мнению. В результате был введен критерий по методу экспертной оценки (Е) с весовыми коэффициентами, определяемыми исходя из нормированных результатов опроса экспертов:

Е = max ([0 , 375 •М + 0 , 275 • F + 0 , 25 • S + 0 , 1 • D ] , Т ) .

После сортировки весовых коэффициентов из метода экспертной оценки был введен критерий по методу лексикографического упорядочивания (L):

L = max ([0 , 9 •М + 0 , 09 •F + 0 , 009 •S + 0 , 001 • D ] ,Т ) .

По имеющемуся набору данных с результатами моделирования 2300 исполнений были вычислены скалярные критерии. Найдено наименьшее значение среди результатов каждого критерия и построен сводный лепестковый график распределения базовых критериев (рис. 5).

Характерно, что для каждого скалярного критерия в разрезе базовых критериев получилось свое уникальное наилучшее исполнение, а не единственное для всех. Для обхода этой проблемы можно выбрать, к примеру, 10 лучших исполнений каждого скалярного критерия и найти пересечение четырех полученных массивов для поиска исполнения, удовлетворяющего всем критериям. На практике этот способ не сработал из-за того, что скалярный критерий построенный по методу лексикографического упорядочивания практически игнорирует базовый критерий сложности. Если исключить его из рассмотрения, то среди наилучших 10 исполнений по каждому оставшемуся скалярному критерию пересечение присутствует в экземпляре:

М_ь = 0, 9 кг; Д = 29 Гц; Q_b = 33; M_d = 0, 2 кг; f_d = 23 Гц; Q_d = 3.

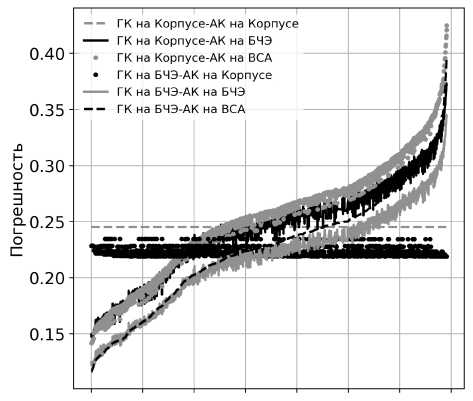
Рис. 4. Влияние расположения ГК и АК в приборе на погрешность решения задачи навигации

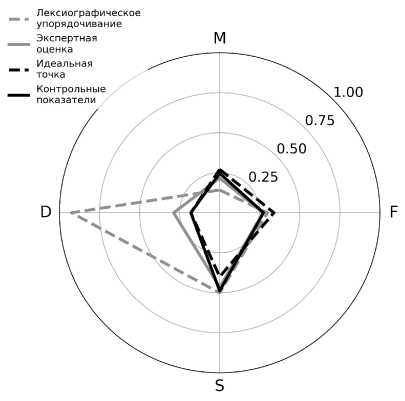
Рис. 5. Наилучший результат, полученный при использовании разных скалярных критериев оптимизации

5.    Решение задачи численными методами

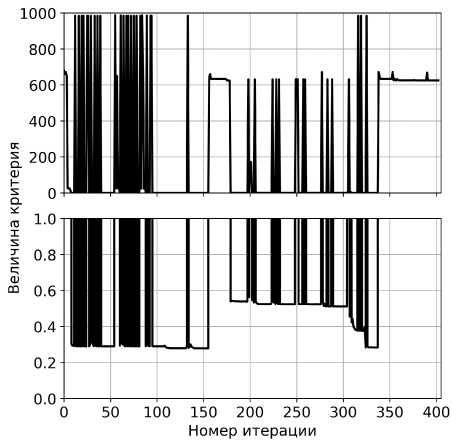
Для дальнейших работ было решено использовать метод контрольных показателей, так как он по своей сути обеспечивает наибольший запас надежности при принятии решения об исполнении САД. Для того чтобы автоматизировать в Python [28] задачу определения оптимального решения и перейти к нахождению глобального минимума за пределами исследованной ранее области, применяются стохастические и детерминированные методы поиска экстремума функции [29]. Для удобства вычислений в скрипт была введена функция преобразования целых чисел из диапазона от 0 до 100 во входные параметры модели. Для поиска решения детерминированным методом использовался пакет scipy. Решение искалось прямым методом сопряженных направлений Пауэлла при помощи функции scipy.optimize.minimize. При использовании других доступных в функции прямых методов («Nelder-Mead», «CG», «COBYLA», «SLSQP») происходило завершение вычислений с признаком успеха после небольшого числа итераций при наличии касаний в ВС А и БЧЭ, т.е. функция не преодолевала барьер. Следующим примененным методом стал квазинью-тоновский метод «BFGS», подразумевающий вычисление градиента функции. Для учета дискретности изменения параметров САД в нем было введено ограничение на выбор шага вычисления градиента только областью целых чисел. Вероятно, из-за этого при его работе наблюдается неустойчивый процесс, проявляющийся как колебания вокруг точки локального минимума (рис. 6).

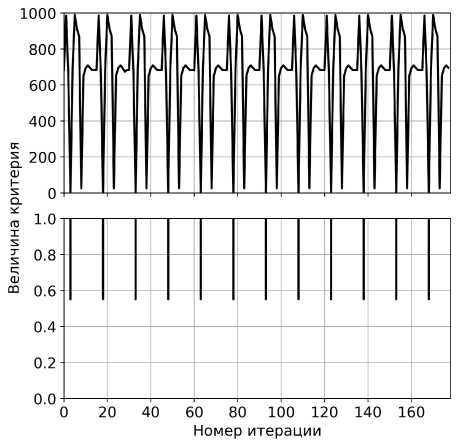
Для поиска решения стохастическим методом также использовался пакет scipy. Решение искалось при помощи распространенного генетического алгоритма, реализованного в функции scipy.optimize.differential_evolution. Изменение величины критерия с увеличением номера итерации приведено ниже. Дополнительно использовался и другой способ решения задачи при помощи генетического алгоритма - применялись пакет deap и функция deap.algorithms.eaSimple. Второй вариант позволяет настраивать условия поиска при решении задачи более подробно. Для обнаружения эффективных исполнений САД в большем диапазоне параметров при использовании deap решение искалось с меньшими вероятностями мутации (0,3) и скрещивания (0,8), чем при использовании scipy - 0,7 и 0,9 соответственно (рис. 7).

а)                                                      б)

Рис. 6. Изменение величины скалярного критерия с увеличением номера итерации при использовании scipy.optimize.minimize (а - «Powell», б - «BFGS»)

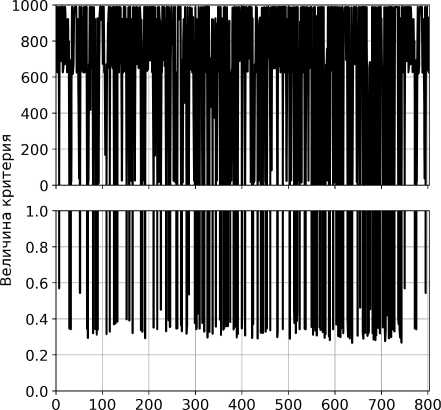
Номер итерации

а)

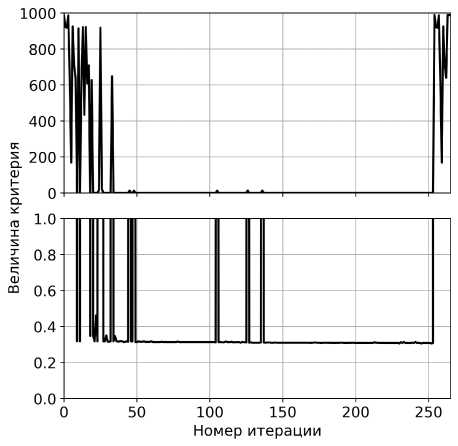
б)

Рис. 7. Изменение величины скалярного критерия с увеличением номера итерации (а - при использовании scipy.optimize. differential evolution, б - при использовании deap.algorithms.eaSimple)

После завершения итерационного моделирования получен набор исполнений для каждого метода, среди которых определено одно наилучшее по критерию контрольных показателей. Параметры наилучшего исполнения были использованы как начальные значения для запуска повторного цикла моделирования. Наилучшие по итогам цикла запусков результаты приведены ниже (табл. 1).

Таким образом оптимальным решением по критерию контрольных показателей, т.е. с точки зрения его удаленности от критичной точки, является следующее исполнение САД:

М_ъ = 0, 8 кг; f_b = 26, 3 Гц; Q_b = 35, 6; M_d = 0, 07 кг; f d = 27, 2 Гц; Q_d = 8, 2.

Таблица!

Результат работы методов оптимизации

Параметр	Перебор	Powell	BFGS	Генетический алгоритм
				De ар	SciPy
Мь, кг	0,9	1,6	1,5	1,6	0,8
fb, Гц	29	25,4	25,3	25,4	26,3
Qb, б/р	33	37	39,4	37	35,6
Md, КГ	0,2	0,2	0,18	0,2	0,07
fd, Гц	23	29,6	29,3	29,6	27,2
Qd, б/р	5	15,2	9,9	9,1	8,2
S, б/р	0,489	0,616	0,588	0,614	0,426
F, б/р	0,273	0,225	0,214	0,224	0,202
M, б/р	0,247	0,183	0,246	0,248	0,251
D, б/р	0,180	0,052	0,080	0,091	0,105
L, б/р	0,251	0,191	0,246	0,249	0,248
Е, б/р	0,308	0,290	0,306	0,317	0,267
Г, б/р	0,319	0,341	0,339	0,353	0,272
С, б/р	0,288	0,239	0,258	0,268	0,237

6.    Заключение

В результате проведенных работ создана комплексная математическая модель, обеспечивающая решение следующих вопросов:

• 1)    задание входного воздействия в форме любого типа полезного или вредного сигнала из приведенных в техническом задании прибора;

• 2)    исследование движения в САД прибора при выбранном входном воздействии и контроль превышения допустимых перемещений в БЧЭ и ВСА;

• 3)    вычисление координат движущегося объекта по законам, закладываемым в типовой алгоритм навигации БИНС;

• 4)    введение базовых и скалярных критериев оценки эффективности исполнения САД;

• 5)    итерационное моделирование с варьированием параметров САД для обнаружения наилучшего исполнения методами многокритериальной оптимизации.

Можно верифицировать матмодель для нахождения оптимальной САД более приближенной к реальности. Однако вследствие технологических и конструктивных ограничений при изготовлении компонентов САД эта работа будет излишней и достаточно применить полученные результаты моделирования для качественной оценки путей улучшения изготовленной в НИИ ИМ САД.

Более перспективным видится применение разработанного математического аппарата для решения других задач оптимизации, более явных и с достаточно изученной математической моделью. Например, для подбора компонентов аналоговых электрических цепей и коэффициентов в цифровых вычислителях для минимизации шумов в выходной информации прибора.