Анализ скорости и кривизны траектории в задаче преследования множества целей
Автор: Дубанов А.А.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 3 т.21, 2021 года.
Бесплатный доступ
Введение. Рассматривается кинематическая модель группового преследования множества целей на плоскости. Преследователи при достижении целей используют метод, подобный параллельному сближению. В отличие от метода параллельного сближения векторы скоростей преследователей и целей направлены произвольно. В методе параллельного сближения мгновенные направления движений преследователя и цели пересекаются в точке, принадлежащей окружности Аполлония. В групповой модели преследования множества целей преследователи стараются придерживаться сети прогнозируемых траекторий.Материалы и методы. В модели поставлена задача достижения целей преследователями в назначенные моменты времени. Она решается методами многомерной начертательной геометрии при помощи эпюра Радищева. Прогнозируемая траектория является составной линией, которая при передвижении цели перемещается параллельно самой себе. На плоскости проекций «Радиус кривизны - значение скорости» выводится допустимый диапазон скоростей преследователя в виде линий уровня (это прямые, параллельные одной из плоскостей проекций). На плоскость проекций «Радиус кривизны - время достижения цели» выводятся образы линий уровня скоростей. Ведется поиск точек пересечения образов линий скоростей с линией уровня назначенного времени. По линиям связи значения точек пересечения опускаются на плоскость «Радиус кривизны - значение скорости». По полученным точкам строим аппроксимирующую кривую и ищем точку пересечения с линией назначенной скорости. В результате получаем значения радиуса окружности при прогнозируемой линии траектории движения преследователя.Результаты исследования. По результатам проведенных исследований созданы тестовые программы и изготовлены анимированные изображения в системе компьютерной математики.Обсуждение и заключения. Данный метод построения траекторий преследователей для достижения множества целей в заданные значения времени может быть востребован разработчиками автономных беспилотных летательных аппаратов.
Многофакторный анализ, эпюр радищева, цель, преследователь, траектория, радиус кривизны
Короткий адрес: https://sciup.org/142231887
IDR: 142231887 | УДК: 004.021 | DOI: 10.23947/2687-1653-2021-21-3-275-283
Текст научной статьи Анализ скорости и кривизны траектории в задаче преследования множества целей
Funding information: the research is done with the financial support from Buryat State University in 2021 (the innovation grant “Control of a four-link manipulator based on signals received from the neurointerface”).
Введение. Рассмотрим модель расчета траектории преследователя на плоскости, где в каждый момент времени от преследователя до цели строится прогнозируемая траектория, которой постарается придерживаться преследователь (рис. 1).
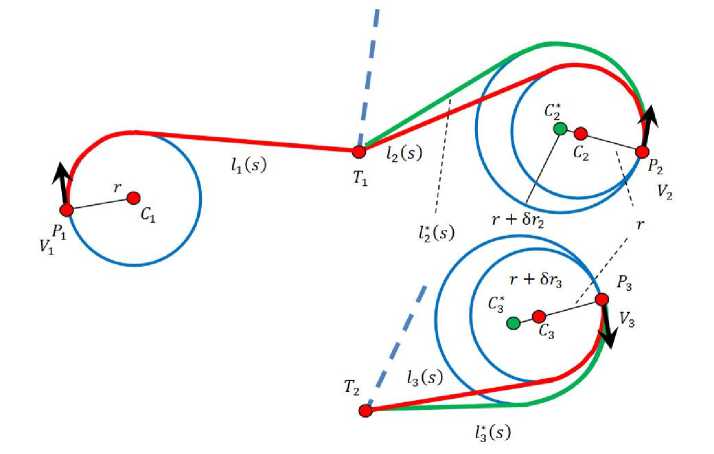
Рис. 1. Групповое преследование множества целей
Кривые 1 1 (s), l2(s), l3(s) состоят из сегмента дуги окружности и прямолинейного отрезка. В нашей модели радиус окружностей и есть ограничение по кривизне прогнозируемых траекторий движения преследователей 1, 2, 3 .
Задачу исследования в данной статье можно описать так: преследователи, двигаясь по однопараметрической сети прогнозируемых траекторий, должны достигать своих целей в назначенные моменты времени, в том числе и одновременно. Для решения выбраны методы многомерной начертательной геометрии с использованием эпюра Радищева. Однопараметрическая сеть (рис. 2) состоит из конгруэнтных линий параллельного переноса. Каждая линия — аналог линии визирования (это прямая, соединяющая преследователя и цель).
XY
1 0,1
XY 1 0,3
XY 2.1
XY
2 0,3
XY
1 0,1
FRAME
(XY )
20,1 FRAME
Y
Target FRAME
• •
-10
-20 -10 0 10 20
XX 1 0,0 , XY 1 0,2 , XY 2 0,2 ,( XY 1 0,0 ) FRAME ,( XY 2 0,0 ) FRAME , X T arg et FRAME
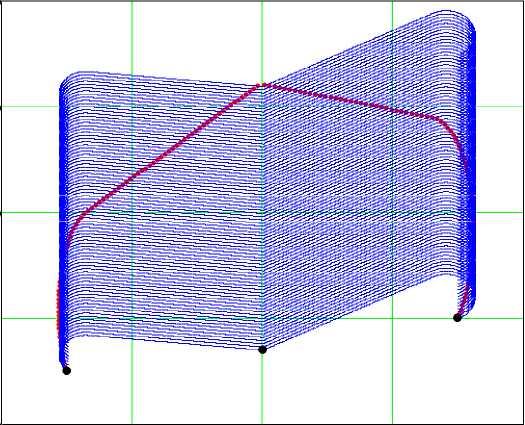
Рис. 2. Однопараметрические сети прогнозируемых траекторий движения преследователей
Для модели выбрана комбинация окружности и прямой. Есть множество вариантов обеспечения ограничений по кривизне (спираль Корню, кубическая парабола, сопрягающаяся с прямой, и т. д.). Для достижения целей преследователи используют метод, аналогичный методу параллельного сближения [1–4]. Однако в нашем случае скорость преследователей направлена произвольно, а в методе параллельного сближения линии скоростей преследователя и цели пересекаются в точке на окружности Аполлония.
В тестовой программе, написанной по материалам статьи, объекты передвигаются по квадрату [-30: 30] х [-30: 30]. Расчет идет в метрах. Исследования проводились для скоростей 20 м/с. Начальный радиус окружностей при прогнозируемых траекториях равен 2 м.
Если в момент начала преследования преследователь находился в точке Pi с вектором скорости Vi, то центр окружности Ci радиуса т будет находиться в точке:
C i = P i ± T •
га
|V i l ■
Затем из точки положения цели T строится касательная к окружности (Ci,Ti) . Совокупность касательной и окружности будет базовой линией прогнозируемой траектории движения преследователя li(s^). Отметим, что в уравнении базовой линии из однопараметрического множества прогнозируемых траекторий параметризация производится от длины дуги.
При новом положении цели T линия li(s) смещается, оставаясь параллельной самой себе (рис. 3).
-
1 Банников А. С. Нестационарная задача группового преследования // Лобачевские чтения : мат - лы 5 - й молодеж. науч. школы - конф. // Тр. математического центра им. Н. И. Лобачевского. Казань : Изд - во Казанского математического общества, 2006. С. 26 – 28.
-
2 Изместьев И. В. Задача преследования маломаневренных объектов с терминальным множеством в форме кольца // Геометрические методы в теории управления и математической физике: дифференциальные уравнения, интегрируемость : мат - лы междунар. конф. Рязань : Изд - во Рязанского гос. ун - та им. С. А. Есенина, 2016. С . 17 – 18.
-
3 Borie R., Tovey C., Koenig S. Algorithms and Complexity Results for Pursuit-Evasion Problems // International Joint Conference on Artificial Intelligence (IJCAI), 2009. P. 59 – 66.
Информатика, вычислительная техника и управление
'<,+1 (s)
Р ..1
*ч
"'

' j+1
l 'j (s)
T'J
Рис. 3. Итерационный процесс расчета траектории преследователя
Допустим, i -й преследователь в момент t j находится в точке Р^. , имея при этом прогнозируемую траекторию движения 1^ (s), соединяющую с текущим положением цели Т^ . В этом случае следующей точкой траектории преследователя будет Р';+г
Р';+1 — это точка пересечения линии Z ' +1(s) , которая соответствует положению цели Tlj+1 в следующий момент времени t j +1 и окружности с центром Р^. и радиусом |v i;. | • At, At = t j +1 — tj. Такова модель построения траекторий преследователя 4, 5.
Рассмотрим задачу группового преследования, когда группа преследователей догоняет группу целей. Будем считать, что каждый преследователь Р ' стремится достичь своей цели Т ' , хотя у некоторых преследователей цели могут совпадать (рис. 1, 2).
Причем преследователь Р ' достигает цели Tt за определенное время t ' , двигаясь с определенной скоростью V ' . Для одновременного достижения целей необходимо равенство всех t ' определенному значению.
Из рис. 1 видно, что для изменения длины базовой линии можно менять радиус касательной окружности. Касательная вводится, чтобы преследователь мог плавно перейти на прямолинейную траекторию. Если бы это было так, то задача была бы сведена к преследованию методом параллельного сближения.
Начальная скорость преследователя направлена произвольно, что позволяет задействовать метод параллельного сближения с соблюдением ограничений по кривизне (рис. 2). Для этого используется составная базовая линия, которая при движении цели перемещается, оставаясь параллельной сама себе, происходит плавный переход к методу параллельного сближения с соблюдением ограничений по кривизне (рис. 3). Рис. 2 дополнен ссылкой на анимированное изображение, где можно посмотреть плавный переход к параллельному сближению 6 .
Цель данной статьи — описание метода, при котором преследователь достигает цели в назначенное время из допустимых значений. Можно рассматривать и одновременное достижение целей группой преследователей [5–9].
Материалы и методы. По результатам исследований разработана тестовая программа одновременного достижения целей преследователями, которую можно посмотреть на ресурсе автора. Предложенный алгоритм реализует итерационную схему расчета траектории преследователя (рис. 3).
В модели принята зависимость для преследователя Р, который достигает цели Т за время t:
t = F(Рs,Ts,np,nт,Vp,Vт,RУ
Здесь Р^Т — координаты точек положения преследователя и цели в момент начала преследования; пр,пт — единичные векторы направления движения преследователя и цели в момент начала преследования; VP,VT — модули скоростей преследователя и цели в процессе преследования; R — радиус окружности, смысл которой показан на рис. 1, 3.
Фактически в модели подсчитывается число шагов, за которые преследователь достигает цели. При известном дискретном промежутке времени число шагов можно сопоставить с реальным временем.
-
4 Дубанов А. А., Севээн А. - К. Э. Кинематическая модель метода параллельного сближения : св - во о гос. регистрации программы для ЭВМ / Бурятский гос. ун - т им. Д. Банзарова. RU 2020665641. № 2020664886 ; заявл. 20.11.2020 ; опубл. 27.11.2020.
-
5 Дубанов А. А., Севээн А. - К. Э. Моделирование траектории преследователя на поверхности методом параллельного сближения : св - во о гос. регистрации программы для ЭВМ / Бурятский гос. ун - т им. Д. Банзарова. RU 2020666553. № 2020664893 ; заявл. 20.11.2020 ; опубл. 11.12.2020.
-
6 Дубанов А. Догнать одновременно. Плоскость 1. URL: https://www.youtube.com/watch?v=7VNHNwCbWrg (дата обращения: 22.05.2021).
Если цель движется прямолинейно и равномерно, то зависимость времени достижения цели в уже начавшемся итерационном процессе можно считать функцией от двух переменных — модуля скорости преследователя и радиуса кривизны окружности:
t = F(.VP,R).
В модели считается, что преследователь движется с постоянной скоростью VP, однако ничто не мешает нам менять значения модуля скорости, как и радиуса кривизны. Допустим, что модуль скорости принимает дискретные значения из ряда VPi,i Е [1:7V], а радиусы окружностей на рис. 1, 3 принимают значения R y , j Е [1:М].
Для дальнейших исследований применяется эпюр Радищева, где используются координатные плоскости (R, V) и (R, t) (рис. 4).
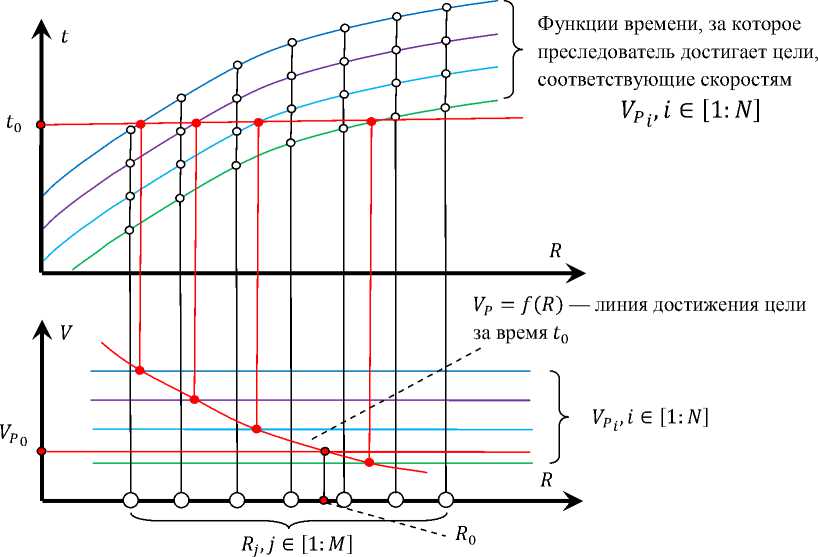
Рис. 4. Определение радиуса окружности на эпюре Радищева
На рис. 4 представлено экспериментальное построение временных зависимостей t^ = F(VPi, Ry) . Графики на плоскости (R, t) показывают, как время достижения цели зависит от радиуса окружности R при фиксированном значении скорости VP .
В качестве одного из оптимизирующих факторов [10-11] на плоскости (R,t) выбирается равенство t = t0, где t0 — требуемое время достижения цели. Далее для решения нашей задачи на плоскости (R,V) в качестве второго оптимизирующего фактора выбирается равенство VP = VPo, где VPo — постоянная скорость преследователя.
В постановке задачи говорится о том, что модуль скорости преследователя является неизменным. Тем не менее построенный ряд значений скоростей необходим для расчета радиуса окружности R0 на плоскости проекций (R, V).
По линиям связи на плоскости проекций (R,V) находятся соответствующие точки пересечения с линиями уровня скоростей VPi (рис. 4). По полученным точкам в тестовой программе выполняется полиномиальная регрессия и в итоге получаем функцию зависимости скорости преследователя от радиуса окружности, при которой происходит достижение цели за время t0.
Затем ищем точку пересечения функции VP = f(R) c линией уровня VP = VPo . Абсцисса точки пересечения R0 и есть искомый радиус окружности, при котором преследователь P за время t0 со скоростью VPo достигает цели Г.
Расчет ведется при условии, что цель движется равномерно и прямолинейно. Если цель изменяет направление или скорость, то рассчитывается новый радиус окружности составной базовой линии (аналог
Информатика, вычислительная техника и управление
линии визирования метода параллельного сближения), ставится новое время достижения при прежней скорости преследователя.
При равномерном и прямолинейном движении цели низший предел времени достижения фиксируется, когда скорость преследователя направлена в точку К на окружности Аполлония (рис. 5). Данное положение рассматривалось в работах Р. Айзекса [12], Л. С. Понтрягина [13], Л. А. Петросяна [14–16], Н. Н. Красовского и А. И. Субботина [17].
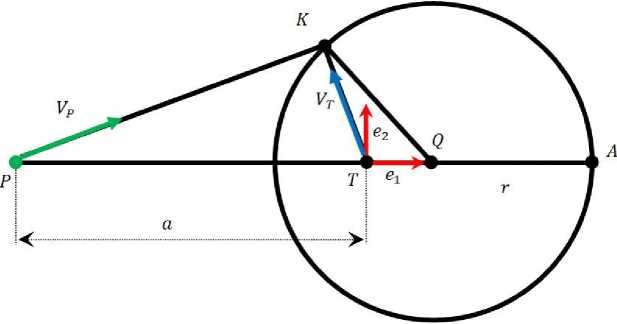
Рис. 5. Окружность Аполлония
Окружностью Аполлония называется геометрическое место точек, отношение расстояний от которых до двух заданных точек — величина постоянная, не равная единице: |РК|/|ТК| = IV p I/IV r l (рис. 5).
При рассмотрении множественного преследования группы целей в тестовой программе делают предварительный расчет траекторий движения преследователей при заданных начальных параметрах. Из времен достижения целей для расчета одновременного достижения выбирается наибольшее время, и оно будет критерием для расчета траекторий остальных преследователей 7 , 8 . Этот момент проиллюстрирован на анимированном изображении, где три преследователя достигают двух целей одновременно 9 .
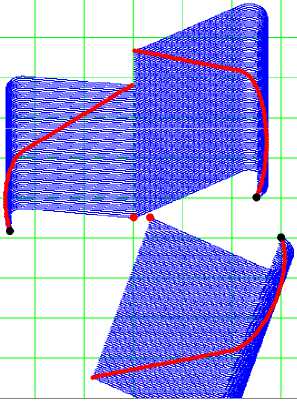
На рис. 6 показано, как для одного из преследователей было установлено более короткое время достижения цели. Рис. 6 также дополнен ссылкой на анимированное изображение, где можно посмотреть достижение целей в различное назначенное время 10, 11, 12 .
Y prediction
Y trajectory
Y Persuer
Y* *
Target
-6
-12
-18
-24
-30
12 18
Persuer Target
-30 -24 -18 -12 -6
XX prediction trajectory
24 30
Рис. 6. Достижение целей в различное назначенное время
-
7 Дубанов, А. А., Севээн А. - К. Моделирование метода параллельного сближения на поверхности : св - во о гос. регистрации программы для ЭВМ. RU 2021618896. № 2021617979 ; заявл. 24.05.2021 ; опубл. 01.06.2021.
-
8 Дубанов, А. А., Севээн А. - К. Модель параллельного сближения на плоскости группы преследователей с одновременным достижением цели : св - во о гос. регистрации программы для ЭВМ. RU 202161892 0. № 2021614416 ; заявл. 30.03.2021 ; опубл. 02.06.2021.
-
9 Дубанов А. NM 1. URL: https://www.youtube.com/watch?v=tdbgoNoby3A ( дата обращения: 22.05.2021).
-
10 Дубанов А. NM 3. URL: (дата обращения: 22.05.2021).
-
11 Дубанов А. NM 2. URL: https://www.youtube.com/watch?v=NNJDJOJT34I (дата обращения: 17.08.2021) .
-
12 Дубанов А. NM 1. (дата обращения: 17.08.2021) .
Результаты исследования. На рис. 7 приведены некоторые результаты многофакторного анализа в задаче одновременного достижения цели двумя преследователями.
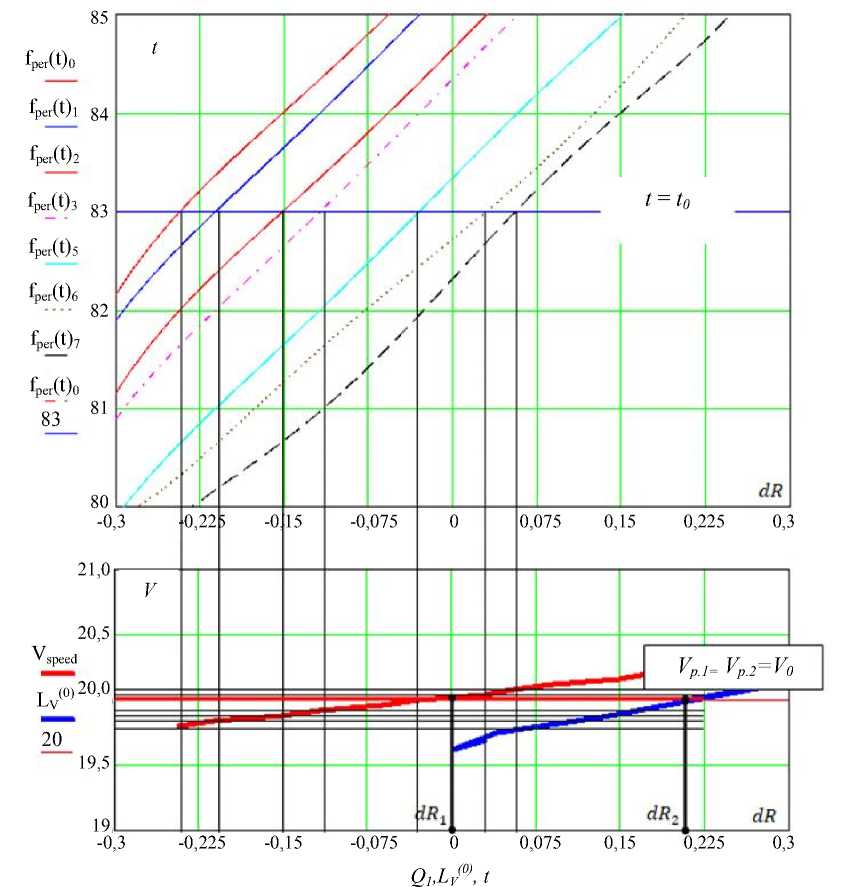
Рис. 7. Результаты многофакторного анализа в задаче одновременного достижения цели двумя преследователями
Цель движется прямолинейно и равномерно. Для каждого преследователя построили ряд допустимых скоростей. Допустимые значения радиуса окружности варьируются при помощи дискретной переменной dR (шкала dR на рис. 7).
На плоскости проекций (dR, t) строим однопараметрическую сеть линий. Каждая линия соответствует определенному значению скорости и выражает зависимость времени достижения цели от приращения радиуса окружности. На рис. 7 показана однопараметрическая сеть линий скоростей одного из преследователей. Для второго в тестовой программе многофакторного анализа построена аналогичная сеть.
Для каждого преследователя выбирается первый оптимизирующий фактор [10–11], отвечающий за одновременное достижение:
t = t o -
Здесь t0 — наибольшее из времен достижения цели, если бы преследователи независимо догоняли цель при таких же начальных условиях.
На плоскости (dR, t) ищем точки пересечения линий уровня t = t0 с линиями скоростей однопараметрической сети. Точки пересечения находятся при помощи встроенных процедур решения уравнений. В системе компьютерной математики MathCAD это может быть процедура root . Найденным точкам пересечения отвечают значения dR и V на плоскости проекций (dR, V).
К полученным точкам на плоскости проекций применяется встроенная процедура полиномиальной регрессии и находится характеристическая кривая зависимости скорости от радиуса окружности составной базовой линии (рис. 1).
Информатика, вычислительная техника и управление
На плоскости проекций (dR, V) рис. 7 изображена такая же характеристическая линия зависимости скорости и для другого преследователя. Далее применяется второй оптимизирующий фактор V 1 = V 2 = V0. В тестовой программе объекты движутся с одинаковыми скоростями. Встроенными средствами компьютерной математики находятся точки пересечения с линией уровня V = V0. Этим точкам соответствуют значения dR 1 и dR 2 .
При запуске итерационного процесса зафиксировано одновременное достижение цели двумя преследователями (аннотация к рис. 2). При этом были найдены значения приращений dR 1 и dR 2 к начальному радиусу окружности и заданы:
-
— значение времени достижения цели t0,
-
— модули скоростей движения V0, с.
В статье описан метод достижения группой преследователей множества целей с возможностью назначать время достижения. Одновременное достижение целей — это частный результат данного подхода, который развивает метод параллельного сближения. При реализации метода в пространстве следует добиться, чтобы векторы преследователя и цели находились в одной плоскости 13 .
Рассмотрим случай преследования в трехмерном пространстве при следующих условиях: мы хотим свести задачу к методу параллельного сближения, но скорость преследователя направлена произвольно. В этом случае базовую линию прогнозируемых траекторий движения преследователя следует строить в плоскости, образованной линией визирования и скоростью преследователя.
Следующий шаг преследователя — точка пресечения сферы с радиусом, равным шагу преследователя, и базовой линии, параллельно перенесенной так, чтобы один ее конец совмещался с точкой положения цели.
Перейдем к вопросу нахождения окружности Аполлония и точки К в трехмерном пространстве. Сама окружность будет находиться в плоскости, образованной линией визирования и скоростью цели. Определим такие параметры окружности Аполлония, как центр окружности (точка Q ), радиус окружности г , точка Аполлония ( А ) и точка К. Для этого учитывают вектор скорости цели, модуль скорости преследователя, положения преследователя и цели. Есть аналитическое решение этой задачи в плоской системе координат (рис. 5). Центр координат находится в точке положения цели. Вектор абсцисс будет единичным вектором вдоль линии визирования, соединяющей положения преследователя и цели. Вектор ординат будет перпендикулярным вектору абсцисс, но в плоскости, образованной линией визирования и вектором скорости цели.
Обсуждение и заключение. Использованные в данной работе методы многомерной начертательной геометрии основаны на вариации модулей скоростей и радиусов кривизны окружностей. При этом по условиям задачи модули скоростей преследователей являются неизменными.
В статье приняты во внимание результаты, достигнутые в работах [18, 19, 20].
Предложенный подход позволяет анализировать модули скоростей и направлений начального движения.
Модель четырехмерного пространства, представленную в работах В. П. Болотова (гиперэпюр Болотова) 14 , следует задействовать для анализа:
-
— модулей скоростей,
-
— радиусов окружностей, прилегающих к преследователям,
-
— начальных направлений движения преследователей.
Приведенные в статье результаты исследований могут быть востребованы разработчиками беспилотных летательных аппаратов, которые выполняют групповые согласованные задачи. Роль оператора наведения может быть сведена к указанию целей и контролю выполнения задач.
Список литературы Анализ скорости и кривизны траектории в задаче преследования множества целей
- Банников, А. С. Некоторые нестационарные задачи группового преследования / А. С. Банников // Известия Института математики и информатики Удмуртского государственного университета. — 2013. — № 1 (41). — С. 3-46.
- Петров, Н. Н. Групповое преследование в рекуррентных дифференциальных играх / Н. Н. Петров, Н. А. Соловьева // Известия Института математики и информатики Удмуртского государственного > университета. — 2012. — № 1 (39). — С. 99-100.
- Благодатских, А. И. Конфликтное взаимодействие групп управляемых объектов / А. И. Благодатских // Ижевск : Изд-во Удмуртского ун-та, 2009. — 263 с.
- Благодатских, А. И. Почти периодические конфликтно управляемые процессы со многими участниками / А. И. Благодатских // Известия Российской академии наук. Теория и системы управления. — 2007. — № 2. — C. 83-86.
- Ибрагимов, Г. И. О некоторых достаточных условиях оптимальности времени преследования в дифференциальной игре со многими преследующими / Г. И. Ибрагимов, Б. Б. Рихсиев // Автоматика и телемеханика. — 2006. — № 4. — С. 16-24.
- Пашко, С. В. Гарантированное время преследования для стратегии параллельного сближения в случае равенства скоростей игроков / С. В. Пашко // Компьютерная математика. — 2014. — № 1. — С. 140-149.
- Пашко, С. В. Гарантированное время преследования для стратегии параллельного сближения / С. В. Пашко // Доповщ Нацюнально! академп наук Украши. — 2014. — № 4. — С. 43-48.
- Пашко, С. В. Максимальное время преследования для стратегии параллельного сближения // С. В. Пашко, А. Л. Яловец // Проблеми програмування. — 2014. — № 4. — С. 78-93.
- Волков, В. Я. Графические оптимизационные модели многофакторных процессов / В. Я. Волков, М. А. Чижик. — Омск : ОГИС, 2009. — 101 с.
- Пашко, С. В. Сложность задач оптимизации преследования на плоскости / С. В. Пашко // Проблемы управления и информатики. — 2013. — № 3. — С. 27-39.
- Пашко, С. В. Численные методы решения задач оптимизации преследования / С. В. Пашко, A. Л. Яловец // Проблеми програмування. — 2013. — № 4. — С. 74-85.
- Айзекс, Р. Дифференциальные игры/ Р. Айзекс. М. : Мир, 1967. — 480 с.
- Понтрягин, Л. С. Линейная дифференциальная игра убегания / Л. С. Понтрягин // Труды МИАН СССР. — 1971. — Т. 112. — С. 30-63.
- Петросян, Л. А. Дифференциальные игры преследования / Л. А. Петросян. — Ленинград : Изд-во ЛГУ, 1977. — 222 c.
- Петросян, Л. А. Преследование на плоскости / Л. А. Петросян, Б. Б. Рихсиев. — Москва : Наука, 1991. — 94 c.
- Петросян, Л. А. Теория игр / Л. А. Петросян, Н. А. Зенкевич, Е. В. Шевкопляс. — Санкт-Петербург : БХВ-Петербург, 2012. — 424 с.
- Красовский, Н. Н. Позиционные дифференциальные игры / Н. Н. Красовский, А. И. Субботин. — Москва : Физматлит, 1974. — 456 с.
- Samatov, B. T. The pursuit-evasion problem under integral-geometric constraints on pursuer controls / B. T. Samatov // Automation and Remote Control. — 2013. — Vol. 74 (7). — P. 1072-1081.
- Multi pursuer differential game of optimal approach with integral constraints on controls of players / Gafuijan Ibragimov, Atamurat Sh. Kuchkarov, Fudziah Ismail, Norshakila Abd Rasid // Taiwanese Journal of is Mathematics. — 2015. — Vol. 19 (3). — P. 963-976. 10.11650/tjm.19.2015.2288 |
- Petrov, N. N. Group pursuit with phase constraints in recurrent Pontryagin's example / N. N. Petrov, N. A. Solov'eva// International Journal of Pure and Applied Mathematics. — 2015. — Vol. 100 (2). — P. 263-278. ^ 10.12732/ij pam.v 100i2.8


