Анализ смертности ликвидаторов последствий аварии на ЧАЭС по данным Национального радиационно-эпидемиологического регистра (НРЭР) за период наблюдения 1992-2010 годы

Смертность является наиболее важной и информативной характеристикой состояния здоровья популяции или когорты. Смертность и заболеваемость ликвидаторов регулярно анализировали по мере накопления данных наблюдений в Национальном радиационноэпидемиологическом регистре (НРЭР). Результаты анализа опубликованы в работах [1-3, 8-11].

Для получения объективных оценок исследуемого процесса необходимо его изучать различными и независимыми методами. Смертность и заболеваемость ликвидаторов (жителей России), облучённых после аварии на ЧАЭС, была в основном исследована путём анализа зависимости доза-эффект с применением регрессионных моделей риска.

Тем не менее, представляется полезным провести анализ смертности другими независимыми методами, применяемыми в современной эпидемиологии, например, сравнением облучённой и необлучённой групп людей, где неопределённости оценки радиационного риска, связанные с дозами облучения, существенно уменьшаются.

Одним из таких методов анализа выживаемости (смертности) является подход Каплана-Мейера (KM) [12], широко применяемый в медицинской практике для оценки эффективности методов лечения и выживаемости. Этот метод в принципе основан на оценке с использованием максимума непараметрической функции правдоподобия [7, 12, 14], что является его опреде-

Горский А . И .* – вед . научн . сотр ., к . т . н .; Максютов М . А . – зав . лаб ., к . т . н .; Туманов К . А . – научн . сотр ., к . б . н ., Кочергина Е . В . – зав . лаб ., к . м . н .; Иванов В . К . – Председатель РНКРЗ , зам . директора по научн . работе , член - корр . РАМН . ФГБУ МРНЦ Минздрава России .

лённым достоинством, так как не требует привлечения и обоснования моделей риска. Кроме того, этот метод достаточно прост для расчётов и даёт возможность наглядного анализа динамических характеристик сравниваемых групп. Метод КМ даёт точные оценки в случае, когда рассматривается только один процесс (смертность от изучаемой причины) и при этом практически до полной смертности всех членов наблюдаемой группы. В реальности этот процесс сопровождается конкурирующими событиями смертности от других причин, выбытием из группы наблюдения до возможной смерти, цензурированием справа, когда члены группы живы за период наблюдения и неизвестен их жизненный статус в будущем. В подходе КМ все потери наблюдения, не связанные с изучаемой причиной смерти, учитываются индикатором цензурирования при расчёте времени наблюдения. Как показано в [6, 14], такой подход может давать смещённые оценки риска смерти для рассматриваемой причины в присутствии конкурирующих рисков. Этого недостатка не лишён и подход, основанный на пропорциональной модели Кокса [4], хотя там также говорится об осторожности при применении таких моделей для конкурирующих процессов. Один из подходов для решения данной проблемы приведён, например, в [5].

В рамках данной работы рассмотрим оба подхода: как без учёта конкурирующих рисков – обычным регрессионным методом, так и модифицированным подходом (с учётом конкуренции рисков), описанном в [6, 14] применительно к анализу смертности ликвидаторов от разных причин, по медико-дозиметрическим данным, накопленным в НРЭР с 1992 по 2010 гг. Заметим, что такой подход применяется впервые к когортам большой численности, каковой является когорта ликвидаторов.

Для оценки влияния эффекта облучения на смертность разделим всю когорту на две, используя определённый дозовый критерий (граничную дозу), так чтобы численности этих когорт были близки. Известно, что такое разбиение, как правило, даёт максимальную статистическую мощность исследования. Условно будем считать когорту с меньшими дозами как необлучённую (контроль), а с большими дозами – как облучённую, и будем сравнивать разность и отношение рисков в этих когортах.

Статистический метод анализа

Смертность от всех причин

Для оценки смертности от всех причин методом КМ будем придерживаться материалов, содержащихся в публикации [13].

Весь период наблюдения М разбивается на К временных интервалов. Представим, что имеется определённая вероятность s k прожить к-ый интервал времени и не умереть.

Будем считать, что число случаев смерти в период времени t k , равно А k , число выживших в этот период времени – B k , а N k =A k +B k – полное число наблюдаемых членов популяции за период времени t k (члены популяции, умершие в предыдущие моменты времени, не учитываются). В качестве величины N будем рассматривать годовое число человеко-лет наблюдения.

Тогда вероятность пройти весь период М и не умереть (выжить) S М будет равна:

B

S M = П s k ⁼Птр -                                    (1)

k k Nk что следует из аксиомы для вероятности совместного появления независимых событий. Тогда:

R M = ¹ - S M ,                                                      (2)

будет риском смерти в момент времени M .

Остаётся определить доверительные интервалы для оценки вероятности выживания (риска смерти) в момент времени М. Согласно [7] (формула Гринвуда), дисперсия (Var – Vari-

SR ance) для логарифма отношения (логита - logit(S))= ln(—M) и для logit(R)= ln(—M) равна:

R M              ^S M

M

V = Var ( logit ( S m )) = Var (ln( S m )) = -2- • £ (— - —) .            (3)

R m    R m k =1 B k N k

Выражение (3) получено с использованием дельта-метода разложения непараметрической функции правдоподобия для метода КМ в ряд Тейлора и ограничением членов первого порядка малости.

Тогда верхний и нижний доверительные пределы (±) для вероятности избежать смерти в момент времени М определяются по формуле:

S low = expit ( logit ( S m )) ± z • Var ( logit (S m )) ⁰’⁵ .                        (4)

Здесь expit – обратное преобразование logit :

expit ( a ) =     ¹    .                                                         (5)

1 + e

Для риска смерти доверительные пределы определяются как 1 - S ow .

z =1,645 для 90 % доверительного предела, или z =1,96 для 95 % доверительного предела – квантили стандартного нормального распределения.

При дальнейших расчётах для большей надёжности оценок будем использовать 95 % доверительные пределы.

Предположим, что мы имеем две популяции: необлучённая и облучённая, для которых определили соответствующие значения S 0 , R 0 и S 1 , R 1 в определённый момент времени, а V 0 и V 1 – дисперсии их логитов, тогда приближённая дисперсия для разности рисков R 1 -R 0 будет равна:

Var ( R 1 - R о ) = R 2 • S ² • V , + R 2 • S 2 • V ₀ .                                (6)

Для логарифма отношения рисков:

Var (ln( R ¹ )) = S 2 • V _l + S 2 • V о .                                          (7)

^R о

Разница рисков R 1 – R 0 представляет собой избыточный абсолютный риск, отношение R 11 R 0 для редких заболеваний, к которым можно отнести онкосмертность, - относительный риск.

Для сравнения смертности в двух группах часто используется лог-ранк тест. Он основан на сравнении функций риска в двух группах, в определённые моменты времени в рамках гипо- тезы, что риски в сравниваемых группах одинаковы. Используя приведённую нотацию, выражение для лог-ранк статистики в момент времени k будет иметь вид:

∑k (A1j -E1j)

Z k = ^{j =1} _k            ,                                                             (8)

( ∑ V j ) ^0,5

j =1

где A1 j – число случаев в первой сравниваемой группе (облучённой) в момент времени j , E1 j – ожидаемое число случаев в первой группе, при условии, что риски смертности в двух группах одинаковы, V – дисперсия разности А 1 j и Е 1 j в момент времени j . Величина Е 1 j равна A j ⋅ N1 j /N j , где A j =A1 j +A0 j , N j =N1 j +N0 j , величины N1 j и N0 j соответственно равны числу человеко-лет под риском в момент времени j . Дисперсия V j определяется как:

N1j      N1j

Aj ⋅    j ⋅ (1 - j)⋅(N -A)

V j =

j Nj ( Nj ) ( j j)

Nj-1

Лог-ранк статистика имеет приблизительно стандартное нормальное распределение.

Если Z>z α , где z α – верхний квантиль нормального распределения, то нулевая гипотеза о равенстве распределений отклоняется при заданном α уровне значимости.

Риск смертности от определённой причины при конкуренции рисков

В этом случае для анализа смертности от данной причины используется величина кумулятивной функции смертности (CIF – cumulative incidence function) [6, 14]. Для конкурирующих рисков использование выживаемости от данной причины (в смысле КМ) не имеет вероятностной интерпретации и может привести к смещению оценок риска, а именно к завышению. Функция выживаемости S(t)=1 – (CIF ev (t)+CIF cr (t)) , где индекс ev относится к оцениваемой функции, а cr – к конкурирующим рискам. Так как CIF cr >0 , 1 – CIF ev (t)>S(t) , то есть в присутствии конкурирующих рисков величина P (вероятность смерти) уменьшается. Величина CIF(t) представляет собой риск или вероятность смерти от интересующей причины в период времени от 0 до t . Величина CIF для причины смерти m определяется для каждой сравниваемой группы, для первой группы:

k A1m

С IF 1 k ^m = ∑    ^j ⋅ S 1 ^K j - ^M 1 ,                                             (10)

j=1 N1j где S1Kj -M1 – функция выживаемости (в смысле КM) для всех причин смерти для первой группы. Для второй группы выражение аналогично для соответствующего индекса группы.

Дисперсия V для CIF для каждой группы и причины смерти m определяются из выражения [14] для первой группы:

v (cif i m ) = t (cif i m j =1

- CIF1m )2 •

___Ab___+N1 j • (N1 j - Aj)

+ ts 1IKM1 • A1m j=1

N1 - A1m• (—j----—(N1j)3

) - 2 • t (CIF 1m j=1

- cif1m) • s 1km j 1       j-1

A1mj

• (N1 j )2 ■

Здесь A1 j = t A1mj – полное число смертей в момент времени j. Доверительные преде-m лы CIFlUW для всех причин смерти совпадает с оценкой 1 - Sow по формуле Гринвуда (4), то есть формула (11) переходит в формулу (4).

Модифицированная версия лог-ранк статистики для случая конкурирующих рисков имеет вид [14]:

к            A1m + A 2 m)

у ( A1 m - r 1 m • (— j— ^j— )

∑ j j m m

Zm k =

(∑k Vj)0,5

j =1

m      (1 - cif1m a

RAm = NA • -_______j-^ R2 = N2 •

^{R 1} j N ¹ j km™    ^{, R2} J    N² J

S ¹ j -1

(1 - CIF2 mJ

KM s 2 j-1

.

Величина дисперсии V определяется по формуле (9) с учётом рассматриваемой причины смерти.

Определение необходимого размера популяции для выявления относительного риска при заданном уровне значимости а и статистической мощности в двух сравниваемых группах одинаковой численности

Данный подход – сравнение смертности в двух группах одинаковой численности – даёт возможность приближённо определить требуемый размер общей когорты и число случаев, необходимых для выявления относительного риска с заданным уровнем значимости критерия а (уровня значимости) и мощности критерия 1- в (обычно величина в выбирается равной 0,2). Этот подход может быть полезен для определения времени наблюдения за когортой на основании имеющихся данных, когда исследуемые риски могут стать значимыми при заданном уровне значимости. При учёте конкуренции рисков воспользуемся описанием подхода, приведённого в [14].

Необходимое число интересующих нас событий n в обеих сравниваемых группах одинаковой численности, для того чтобы определить относительный риск в для уровня значимости а и мощности (1- в ), определяется из уравнения:

n = (

z1-а/2 + z1-в )2 1п(в)

где z – квантили нормального распределения.

Требуемая численность общей когорты N определяется как:

N = n / P ,                                                             (15)

где P – вероятность интересующего нас события. Определим вероятность P1 в первой сравниваемой группе в присутствии конкурирующих рисков как [14]:

fp

P1=1- 1 ⋅ (1- CIF1(u)) du.                                             (16)fp 0

Здесь fp – период наблюдения, накопления данных, CIF – кумулятивная функция, определяемая уравнением (10). Аналогично определяется и P2 , а P = P1 + P2 . Тогда из (15) определяем N .

Для оценки риска стандартными регрессионными методами использована модель пропорциональных рисков Кокса. Изложение этого подхода приведено, например, в [4, 9].

Используем описанные подходы для анализа общей смертности и смертности от отдельных причин в когорте ликвидаторов последствий аварии на ЧАЭС, жителей России.

Общее описание когорты ликвидаторов

Рассмотрена выборка из когорты ликвидаторов (мужчины) из 6 регионов европейской части России за период наблюдения с 1992 по 2010 гг. (Центрально-Чернозёмный, СевероКавказский, Северо-Западный, Поволжский, Волго-Вятский, Уральский). Информация, поставляемая региональными центрами из этих регионов, отличается надёжностью и полнотой. Годы въезда в зону облучения – 1986-1990. Нижняя и верхняя границы наблюдения выбраны, исходя из особенностей сбора медико-дозиметрической информации. Верхняя граница выбрана, чтобы учесть 3-годичный лаг в полноте данных регистра. Нижняя – учитывает период стабилизации процессов накопления данных в НРЭР. Интервал документальных доз – 1,0-500 мЗв. Интервал возраста при облучении – 18-70 лет. Интервал достигнутого возраста – до 85 лет.

Отметим, что для корректной оценки смертности методом КМ необходимо, чтобы сравниваемые когорты имели близкие возрастные распределения в начале наблюдения. Данное условие сравнительно редко реализуется на практике, но эту проблему можно решить имитационными методами с использованием генераторов псевдослучайных чисел.

Процедура выравнивания возрастных распределений производилась следующим образом:

• 1)    на основании дозового критерия когорта разделяется на две с одинаковой численностью;

• 2)    в каждой когорте определяется число людей в возрастных группах;

• 3)    выбирается возрастная группа в двух когортах, где имеется избыток числа ликвидаторов по отношению к другой группе. Из этой возрастной группы с помощью генератора случайных чисел выбирается число членов этой возрастной группы, равное численности другой группы.

Исходная численность когорты согласно перечисленным критериям – 74814 человек. Основные характеристики сформированных когорт приведены в таблице 1. Граничная доза для определения облучённой и условно необлучённой групп (контроль) – 94 мЗв. Средняя доза во всей когорте равна 109,1 мЗв.

Таблица 1

	Контрольная группа	Облучённые
Исходная численность	37489	37325
Численность после имитационного моделирования	29049	29071
Число случаев смерти (все причины)	7807	8028
Средняя доза (мЗв)	43,7	171,0
Число человеко-лет наблюдения	450878	455287

Основные характеристики сравниваемых когорт

На рис. 1 приведено возрастное распределение в 1992 г. для обеих когорт до и после имитационного моделирования. Из рисунка видно, что распределения совпадают после имитационного моделирования. Следует отметить, что имитационное моделирование привело к уменьшению численности когорты на 26 %, что уменьшает статистическую мощность анализа.

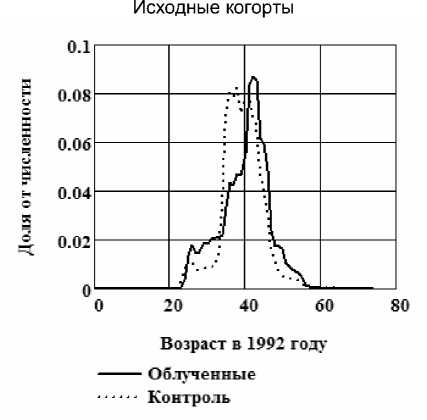
Имитационное моделирование

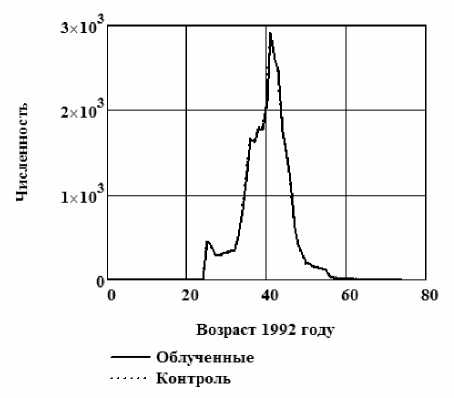
Рис . 1. Возрастное распределение в когортах ликвидаторов до и после имитационного моделирования.

Рассмотрим результаты анализа смертности в сравниваемых когортах как для смертности от всех причин, так и для отдельных причин смерти.

Все причины смерти

Для расчёта функции дожития, отношения и разности рисков использовался обычный подход КМ, описанный в разделе «Методы статистического анализа». Функция выживаемости для обеих групп приведена на рис. 2.

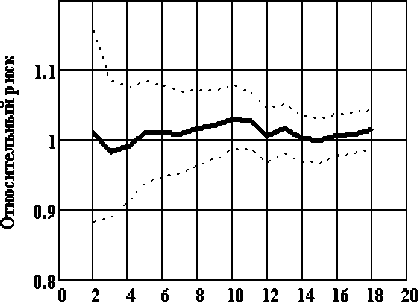
Как следует из рис. 2, кривые выживаемости практически совпадают, что говорит о близости интенсивности процессов смертности от всех причин. Полученный вывод подтверждается результатами оценки динамики относительного и абсолютного риска в сравниваемых когортах, приведённых на рис. 3 с 95 % доверительными пределами. Относительный риск близок к единице, а абсолютный – к нулю. Нижний доверительный предел для относительного риска меньше единицы, а для абсолютного риска меньше нуля, что означает отсутствие статистической значимости при заданных доверительных пределах. В обеих когортах осталось в живых около 70 % от численности в 1992 г. Следует отметить устойчивость оценок риска практически за весь период наблюдения.

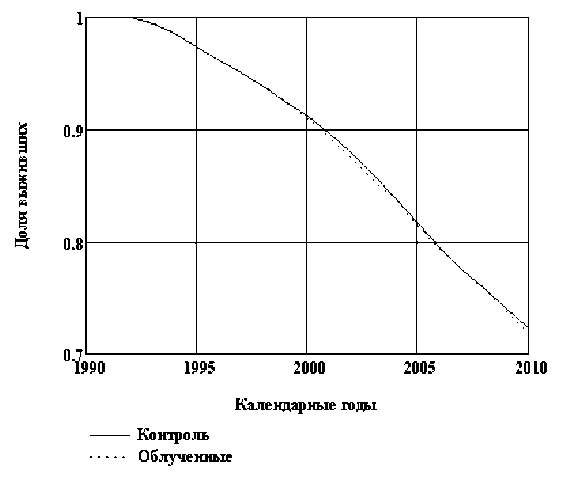
Рис . 2. Функция выживаемости в сравниваемых когортах ликвидаторов.

Время наблюдения, годы

Риск

..... 95% ДП

..... 95% ДП

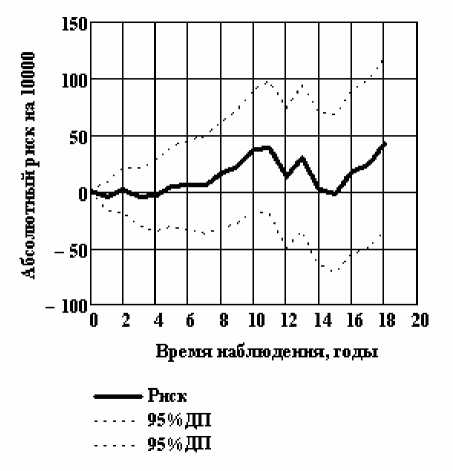
Рис . 3. Динамика относительного и абсолютного риска в сравниваемых когортах.

Значение относительного риска в 2010 г. равно 1,02 (95 % ДП: 0,99; 1,04), величина p по результатам лог-ранк теста равна 0,02.

Смертность от отдельных причин

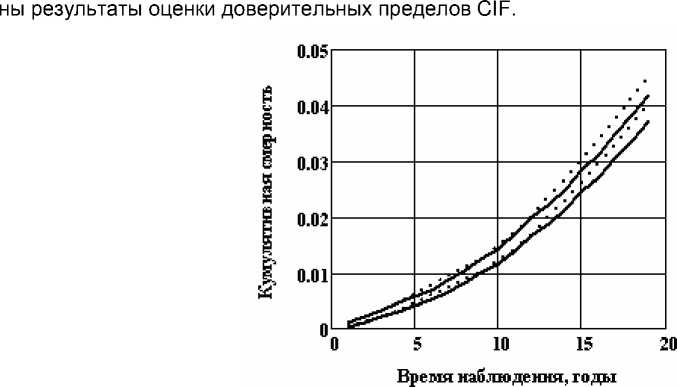
Рассмотрим более детально смертность от солидных раков. Число солидных раков в сравниваемых когортах равно 1044 в контроле и 1147 в облучённой когорте. На рис. 4 приведе-

----95% ДП контроль

----95% ДП контроль

..... 95% ДП облученные

..... 95% ДП облученные

Рис . 4. Динамика доверительных пределов CIF солидных раков в сравниваемых когортах.

Значение CIF в 2010 г. равно 0,04. Из рис. 4 следует, что смертность от солидных раков в облучённой группе больше, чем в необлучённой. На рис. 4 видно, что доверительные пределы для CIF пересекаются, характер отличия доверительных пределов свидетельствует о наличии эффекта облучения, но в рамках выбранного значения α эффект, строго говоря, статистически не значим.

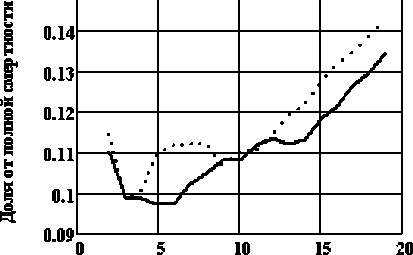
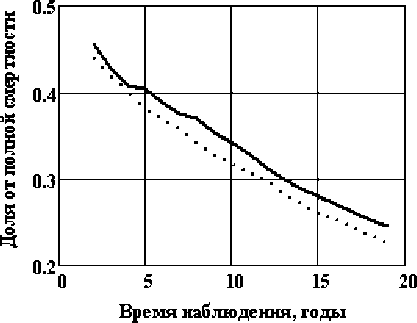
На рис. 5 приведено изменение доли смертей от рака в смертности от всех причин в сравниваемых когортах.

Время наблюдения, годы

Контроль

Облученные

Рис . 5. Динамика доли онкологической смертности от полной смертности.

Согласно рис. 5, доля онкологических смертей в 2010 г. составляет 13-14 %, причём в облучённой группе эта доля устойчиво выше, что также является качественным признаком эффекта облучения. На рис. 6 для иллюстрации приведена динамика относительного и абсолютного риска.

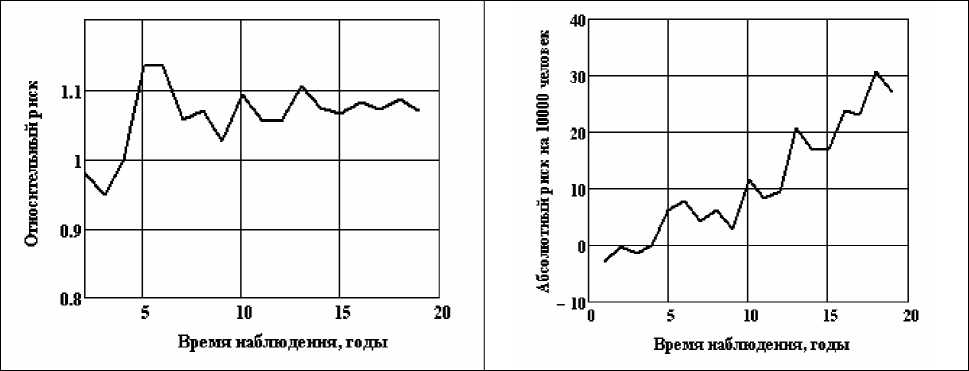
Рис . 6. Динамика относительного и абсолютного риска.

Из рис. 6 следует, что значения относительного риска устойчивы за последние 5 лет наблюдения и равняются, примерно, 1,07. Значения избыточного абсолютного риска везде положительны. Формально, распределение абсолютного риска по годам даёт избыточное число смертей от рака во времени в облучённой когорте по отношению к контролю. Тогда в 2010 г. избыточное число равно 31 случаю смерти на 10000 человек или для всей облучённой когорты численностью 37325 человек – 115 случаев. В рамках гипотезы, что избыток смертей обусловлен облучением, это число радиогенных раков.

Результаты оценки лог-ранк теста, как с учётом, так и без учёта конкуренции рисков, практически совпадают. В данном случае вывод о наличии эффекта облучения аналогичен выводам при анализе доверительных пределов. Это означает, что для когорт с рассматриваемой численностью (несколько десятков тысяч человек) результаты оценки риска при учёте конкурирующих рисков совпадают с результатами, полученными с использованием обычных подходов без учёта конкуренции рисков.

Рассмотрим результаты оценок риска для всей когорты с использованием регрессионного подхода, так как в данном случае используется вся информация о когорте и статистическая мощность исследования повышается.

В таблице 2 приведены оценки риска для всей когорты (численность 74814 человек) с использованием модели Кокса.

Статистически значимые риски наблюдаются для смертности от всех причин, от солидных раков, от болезней системы кровообращения и для отдельных причин, входящих в данную рубрику: гипертензии (I10-I15) и ишемической болезни сердца (I20-I25). Необходимо отметить значимую обратную дозовую зависимость смертности от травм и отравлений. Смертность среди ликвидаторов с меньшими дозами больше, чем среди ликвидаторов с большими дозами. Данный феномен требует дополнительного исследования.

Таблица 2

Результаты оценки риска для всей когорты для различных причин смерти ( регрессионный метод )

Результаты оценки риска для двух когорт как с учётом , так и без учёта конкуренции рисков

Причина смерти	Код МКБ-10	Число случаев	ERR на 1 Зв (95 % ДП)	Величина p
Все причины	-	20183	0,23 (0,02; 0,45)	0,01
Солидные раки	С00-С80	2821	0,57 (0,00; 1,22)	0,02
ЗНО органов дыхания	С30-С39	1163	0,60 (-0,26; 1,66)	0,13
ЗНО органов пищеварения	С15-С26	940	0,56 (-0,37; 1,71)	0,20
Болезни системы кровообращения	I00-I99	8030	0,46 (0,12; 0,84)	0,00
Болезни органов дыхания	J00-J99	1102	0,26 (-0,59; 1,31)	>0,5
Болезни органов пищеварения	K00-K93	1428	0,54 (-0,27; 1,52)	0,15
Цереброваскулярные заболевания	I60-I69	1488	0,41 (-0,33; 1,30)	0,23
Травмы и отравления	S00-T98	4854	-0,42 (-0,77; -0,03)	0,02
Ишемическая болезнь сердца	I20-I25	4728	0,51 (0,06; 1,00)	0,01
Гипертензия	I10-I15	459	2,52 (0,69; 5,15)	0,00

Примечание: ЗНО – злокачественные новообразования.

Таблица 3

Причина смерти	Код МКБ-10	Случаи	ERR/Зв (95 % ДП)	ERR/Зв	p	р	Доля смертей %
1	2	3	4	5	6	7	8
Все причины	-	15825	0,16 (-0,08; 0,40)	0,14	0,16	0,14	100
Солидные раки	С00-С80	2191	0,45 (-0,18; 1,18)	0,56	0,11	0,06	13,7
ЗНО органов дыхания	С30-С39	889	0,72 (-0,28; 1,96)	0,66	0,11	0,32	5,6
ЗНО органов пищеварения	С15-С26	708	0,26 (-0,74; 1,97)	0,64	>0,5	0,14	4,5
Болезни органов дыхания	J00-J99	868	0,32 (-0,65; 1,55)	0,28	0,50	0,34	5,5
Болезни органов пищева-	K00-K93	1136	0,33	0,41	0,43	0,21	7,2
рения			(-0,54; 1,42)
Болезни системы кровооб-	I00-I99	6404	0,47	0,40	0,00	0,02	40,4
ращения			(0,09; 0,90)
Цереброваскулярные забо-	I60-I69	1164	0,49	0,32	0,21	0,26	7,4
левания			(-0,35; 1,52)
Травмы и отравления	S00-T98	3768	-0,51 (-0,90; 0,01)	-0,32	0,05	0,10	23,8
Ишемическая болезнь	I20-I25	3766	0,50	0,54	0,03	0,01	23,8
сердца			(-0,00; 1,06)
Гипертензия	I10-I15	358	2,09 (0,19; 4,91)	1,33	0,01	0,07	2,3

Примечание: ЗНО – злокачественные новообразования.

В таблице 3 представлены оценки риска для двух когорт, использованных в анализе смертности с учётом конкуренции рисков (колонки 5, 7 табл. 3), и этих же когорт, объединённых в одну (численность 58120, табл. 1) с использованием регрессионного анализа (без учёта конкуренции рисков, колонки 4, 6).

Значение ERR на Зв в колонке 5 приближённо определялось как отношение рисков (CIF) в двух когортах, минус единица, делённая на разницу средних доз в когортах (табл. 1) в 2010 г. Как следует из таблицы 3, оценки рисков, полученные с использованием обоих подходов, близки для большинства рассмотренных причин смерти. Значимой является оценка для гипертензии и ишемической болезни. Потеря значимости для смертности от всех причин и солидных раков, по-видимому, обусловлена потерей статистической мощности анализа из-за уменьшения численности когорты, использованной в анализе.

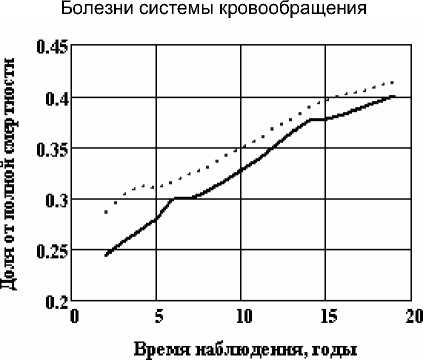
Рассмотрим отдельно причины (кроме солидных раков), для которых риски значимы и число случаев достаточно велико, это травмы и отравления и болезни системы кровообращения (БСК). На рис. 7 приведена динамика доли случаев смерти от полного числа для травм и отравлений и БСК.

Травмы и отравления

Контроль

Облученные

Контроль

Облученные

Рис . 7. Изменение вклада смертности от рассмотренных причин в общую смертность за период наблюдения.

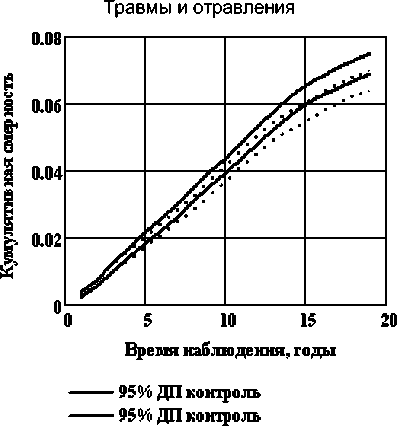
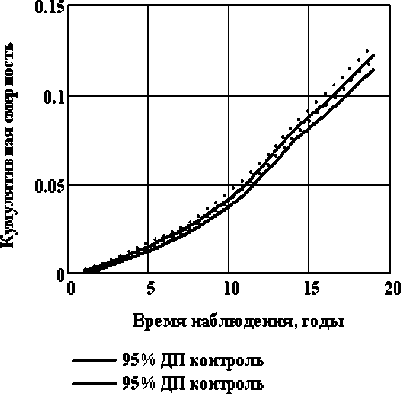
Для травм и отравлений за период наблюдения произошло почти двукратное уменьшение вклада этой причины в общую смертность, причём, как и отмечалось, смертность в группе с большими дозами меньше. Для смертности от БСК интенсивность в группе с большими дозами больше за весь период наблюдения. Биологический механизм данного явления в настоящее время ещё полностью не изучен. На рис. 8 приведены доверительные пределы для кумулятивных функций смертности от травм и отравлений, а также БСК, из которых виден эффект различия между облучённой и необлучённой группами.

95% ДП облученные

95% ДП облученные

Болезни системы кровообращения

95% ДП облученные

95% ДП облученные

Рис . 8. Динамика 95 % доверительных пределов кумулятивной функции смертности для травм и отравлений и болезней системы кровообращения.

Рассмотрим эффективность критерия, описанного уравнениями (14-17), для приближённого определения числа случаев и численности когорты, необходимого для детектирования значимого относительного риска для смертности от БСК. Используемые значения α =0,05 и β =0,2 обычно применяемы в практике. z 1- α /2 + z 1- β =1,96+0,85=2,81. Для БСК в 2010 г. относительный риск θ =1,05. Тогда требуемое число случаев n =3300, величины P1 и P2 , определённые по формуле (16), в 2010 г. соответственно равны 0,045 и 0,048, тогда P =0,093 и N =3300/0,093=32718.

Для смертности от БСК исходная численность рассматриваемой когорты равна 58120 человек, а число случаев – 6404, требуемые величины соответственно равны 32718 человек и 3300 случаев. Это означает, что исходный размер когорты и накопленное число смертей от БСК к 2010 г. позволяют выявлять значимые радиационные риски для смертности от данной причины. Распределение во времени требуемой численности популяции, необходимой для детектирования радиогенного риска смерти от БСК, приведено на рис. 9.

Для расчёта риска смерти от травм и отравлений требуемое количество человек и случаев смерти равно 44019 и 3298, фактическое – 58120 и 3783, что также подтверждает значимый эффект отличия смертностей в сравниваемых группах.

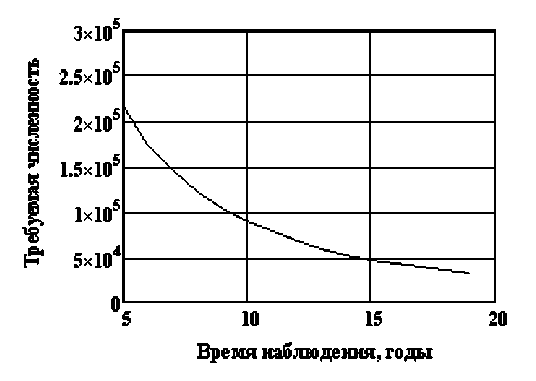
Рис . 9. Распределение требуемой численности когорты для выявления значимых радиогенных рисков смерти от болезней системы кровообращения в процессе наблюдения.

Обсуждение результатов

Проведён анализ смертности среди ликвидаторов на основании информации, накопленной в НРЭР с 1992 по 2010 гг. Для анализа использовались два независимых подхода: обычный регрессионный анализ (модель пропорциональных рисков Кокса) и анализ выживаемости, модифицированный с учётом оценки риска в присутствии конкурирующих причин смерти.

В анализе выживаемости проведено сравнение общей смертности и смертности от разных причин в двух когортах ликвидаторов, сформированных из общей когорты, содержащей данные наблюдений с 1992 по 2010 гг. Для этого, используя имитационное моделирование, из общей когорты были выделены с две субкогорты с одинаковым возрастным распределением на начало анализа (1992 г.) и примерно одинаковой численностью. Для анализа смертности в субкогортах использованы методы анализа выживаемости как без учёта, так и с учётом конкуренции рисков. Для анализа общей смертности применён подход Каплана-Мейера, основанный на максимизации непараметрической функции правдоподобия. Для анализа смертности от конкретных причин использованы подходы, сравнительно недавно описанные в эпидемиологии и применяемые в основном на практике к клиническим исследованиям с малой численностью выборок [6, 14]. В этих исследованиях показано, что некорректный учёт конкуренции рисков может приводить к смещению оценок риска в сравниваемых группах. Поэтому представляет интерес использование этих подходов для групп людей с большой численностью, тем более, что корректное решение проблемы конкурирующих рисков, как правило, не учитывается в большинстве программно-математических пакетов, используемых в эпидемиологических оценках (исключение составляет пакет SAS, где имеются соответствующие процедуры [14]).

Применение подхода, в нашем случае, основанного на сравнении облучённых vs необлу-чённых, имеет свои преимущества и недостатки. Основной недостаток в том, что мы снижаем статистическую мощность исследования, разбивая общий массив данных на две субкогорты по дозовому критерию, хотя и гомогенизированные по возрасту, путём имитационных процедур, при которых также теряется часть информации. К преимуществам данного подхода можно отнести использование непараметрических методов оценивания, позволяющих не привлекать и не обосновывать эпидемиологические модели, понизить требования к неопределённости доз облучения, физической наглядности результатов анализа, в виде динамических характеристик наблюдаемых групп, отражающих внутренние процессы смертности в группах по времени. Кроме того, к достоинствам данного подхода можно отнести также использование интегральных характеристик наблюдаемых процессов, которые дают более устойчивые оценки.

Основные выводы

• 1.    Результаты оценок радиационного риска смертности, полученные обоими методами (модели пропорциональных рисков Кокса и анализа выживаемости с учётом конкуренции рисков), близки для большинства рассмотренных причин смерти.

• 2.    Статистически значимые регрессионные оценки радиационного риска ERR на 1 Зв для полной когорты ликвидаторов из 6 регионов европейской части России (численность – 74814 человек) получены для всех причин смерти – 0,23 (95 % ДП: 0,02; 0,45), солидных раков (МКБ-10: С00-С80) – 0,57 (95 % ДП: 0,00; 1,22), болезней системы кровообращения (МКБ-10: I00-I99) – 0,46 (95 % ДП: 0,12; 0,84).

• 3.    Для когорты, образованной с помощью метода имитационного моделирования (численность – 58120 человек), значимые риски получены для гипертензии (МКБ-10: I10-I15) – 2,09 (95 % ДП: 0,19; 4,91) и ишемической болезни сердца (МКБ-10: I20-I25) – 0,50 (95 % ДП: 0,00; 1,06). Потеря значимости для солидных раков и смертности от всех причин, вероятно, связана с уменьшением численности когорты, обусловленной имитационным моделированием.

• 4.    Получено значимое отличие смертности от травм и отравлений в группах со средними дозами 44 мЗв и 171 мЗв, причём смертность в группе с меньшими дозами больше. Для объяснения данного результата, отмеченного и в более ранних работах, необходимы дополнительные исследования. Для интерпретации результатов смерти от ишемической болезни и гипертензии также необходимы дополнительные данные.

• 5.    Представленные результаты свидетельствуют о необходимости продолжения наблюдения за когортой ликвидаторов и более детального изучения структуры смертности и заболеваемости.