Анализ СМО общего вида с использованием селектирующих функций
Автор: Буранова Марина Анатольевна, Карташевский Вячеслав Григорьевич, Киреева Наталья Валерьевна, Чупахина Лилия Равилевна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 4 т.14, 2016 года.
Бесплатный доступ
В работе представлен метод спектрального решения уравнения Линдли основанный на использовании селектирующих функций для аппроксимации распределений. Суть метода заключается в том, что «восходящие» участки распределений аппроксимируются полиномами малого порядка, а «спадающие» участки - суммой затухающих экспонент с малым числом слагаемых в сумме. Оценка времени ожидания заявки в очереди может быть получена численным решением линейного алгебраического уравнения. Эффективность метода продемонстрирована на примере исследования системы W / P /1, где W - распределение Вейбулла, P - распределение Парето. Метод селектирующих функций позволил заменить распределение Вейбулла распределением, состоящим из двух участков «восходящего» и «нисходящего», аппроксимации которых осуществляются согласно описанному методу. В работе показано, что такая аппроксимация обладает существенно меньшей погрешность по сравнению со случаем, когда используется единая аппроксимация распределения суммой затухающих экспонент.
Системы массового обслуживания, среднее время ожидания заявки в очереди, интегральное уравнение линдли, аппроксимация суммой затухающих экспонент, селектирующие функции, "сшитые" функции, преобразование лапласа
Короткий адрес: https://sciup.org/140191847
IDR: 140191847 | УДК: 519.872 | DOI: 10.18469/ikt.2016.14.4.03
Текст научной статьи Анализ СМО общего вида с использованием селектирующих функций
Анализ характеристик сетевых узлов при обработке трафика, обладающего распределениями с тяжелыми хвостами [1- 2; 7; 9] для интервалов времени между поступлениями пакетов и интервалов времени обработки пакетов, связан с решением интегрального уравнения Линдли [3] для систем массового обслуживания типа G/G/1. При этом для упрощения вычислительной процедуры решения уравнения Линдли спектральным методом часто прибегают к аппроксимации плотностей вероятностей гиперэкспоненциальными распределениями, моделируемыми суммами затухающих экспонент [5; 7-8; 10]. Предложенный в [5] метод аппроксимации распределения суммой затухающих экспонент дает неудовлетворительные результаты по точности аппроксимации на «восходящих» ветвях распределений. Кроме того, аппроксимация «восходящих» ветвей распределений приводит к появлению в сумме затухающих экспонент слагаемых с отрицательными коэффициентами, что нивелирует вычислительные преимущества спектрального метода, обусловленные использованием гиперэкспоненциальных распределений.
Аппроксимация распределения Вейбулла
Для иллюстрации данного утверждения рассмотрим задачу аппроксимации распределения Вейбулла, принадлежащего к классу распределений с тяжелыми хвостами, методом, изложенным в [5]. Например, для распределения Вейбулла с параметрами представленного на рис. 1 пунктиром, аппроксимирующая сумма будет иметь вид
(2) к=\ при некоторых значениях коэффициентов отличающихся друг от друга на несколько порядков [5]. Результат аппроксимации представлен на рис. 1 сплошной линией.
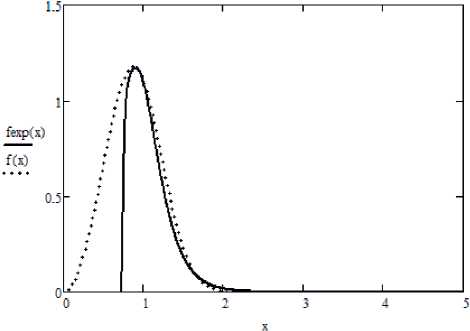
Рис. 1. Аппроксимация распределения Вейбулла: f^ И /ехрИ
Как следует из рис. 1, аппроксимация «восходящей» ветви распределения осуществляется с недопустимо большой ошибкой.
Заметим, что для распределений, в которых отсутствует «восходящая» ветвь, например распределение Парето [4], данная проблема не возникает и число слагаемых в аппроксимирующей сумме (2), как правило, может быть выбрано существенно меньше 10 при сохранении достаточной точности аппроксимации.
Метод селектирующих функций
Для рассмотренного распределения Вейбулла выделим два интервала аппроксимации - и где может быть выбрано, например, как Теперь представим в виде «сшитой» функции через кусочно-нелинейные р!« О<х<хо;
[^2(х), х>х0; (3)
I = jG(x)5z(x,X1,X2)(/x справедливо соотно шение
^1(х) = ^0пхп ’
(4)
/2=1 К фАА = ^9ке"акХ . (5) В (4)-(5) коэффициенты аппроксимации SnA^k определяются соответствующими вычислительными процедурами. Для «сшитой» функции ^с С^) должно выполняться условие нормировки J fc {x)dx = 1. Основным инстру-о ментом «сшивания» является селектирующая функция Sl^X^X^, определяемая как
I
= 0,5
— [1 —
Is gib
— x, )] jG(x)z&
Используя (10) и (8), получаем . (10) j/] (5,x^si(x, 0, x0 ^dx + jk (s, x)si (x, x0, 00) = о 0
с учетом сопряжения в точках «сшивания» в виде:
si Ач, Х;,
х/+1) =
si (хм, х;, хм
) = 0,5. Очевидно, что выражение (3) теперь может быть представлено в виде
/с (х) = фх
(x)sz (х, 0, х0) +
ф^ (x)si
(х, х0, со), (7)
а требуемое для решения уравнения Линдли спектральным методом преобразование Лапласа запишется как
= 0,5< J/, (s,
x)dx + ^ fx (s, x)dx
- j
fx (s, x^dx > +
.° 0 A'o .
+ 0,5< - J/? (s,
XW
+ J/? (5,
x^dx
+ J/? (5,
XW >.
0 0
Вычисляя все интегралы в (11) на основе из- вестных соотношений
Jx”e
Sxdx = n\s 1
FA$) = ^fAxK$xdx = О
Jo
^xne-sxdx =
-A 7?! Xfl
= J/^(5,
x)si
(х, 0,
x0)dx +
о
-А и!
Xq
tS<^
+ j/2(5,x>z(x, х0, со), о где /И2)(5,х) = ^1(2)(х)е"и. Если ввести в рассмотрение функции
\e"atXe-sxdx=——,
0
ak + 5
\e-atXe-sxdx - e"1'^0 ak+s sg(x) = <0,5; х = 0;
sgn
(х) =) О,
х < 0; х = 0; х<0; (9)
e sxdx=
—-—e a, +5
sg(x) = l-sg(x),
для преобразования Лапласа
Fc
(^) получим
^__е-Иоу »!
4
,и+1
2-1
7,| с'>-4 + 1
+
1
e"|ai+5)Vn
^s
Используем (12) в задаче анализа системы массового обслуживания G/G/1 путем решения интегрального уравнения Линдли спектральным методом [3].
Суть метода заключается в представлении выражения ^(-s)S(s)-l в виде ^(-^й)-!--^, где
А(з)
и
B(s)
– пре-
^-й) образование Лапласа плотностей вероятностей промежутков времени между поступлениями заявок на обслуживание в систему и времени обслуживания заявок в системе, соответственно. При этом функции Ч< и Т должны удовлетворять условиям: – Ф+й) – аналитическая функция без нулей в области Ней) > 0;
– Ч^й) – аналитическая функция без нулей в области Re(^) <
D
для некоторого
D > О;
- lim —tl^l - i дЛЯ Re(5) > 0 - ,v| >v. Т_й)
- lim —±— = 1 для Re(s) <
D .
й=" ^
Если функция T+ (s) найдена, то характеристическая функция времени ожидания заявки в очереди ф+й) может быть определена в виде r ^(s) lim— ф (5) = ^^, Ч^й)
время ожидание в очереди г-^Ф.ИЬ
ds
Аппроксимация распределений для анализа системы G/G/1 Рассмотрим применение рассмотренного метода аппроксимации распределений для анализа системы G/G/1. Пусть плотность вероятностей времени обслуживания заявок в системе определяется распределением Вейбулла f k^) с параметрами a = 1,5 и P = 1. Методом селектирующих функций заменим J M на fc W ’ а для плотности вероятностей интервалов времени между поступлениями заявок выберем распределение Парето ab“ W = ^, «>0,b>0, x>0, с параметрами a = 0,5 и b = 1,9.
Пусть плотность
fe
(-К) на интервале (0, x0 - 0,5) аппроксимируется полиномом третьей степени согласно (4) при
N
= 3, 9, = 0; 02 = 3,573; 93 = -4,167 и суммой затухающих экспонент согласно процедуре [5] на интервале йо’”) с параметрами
к = 3,
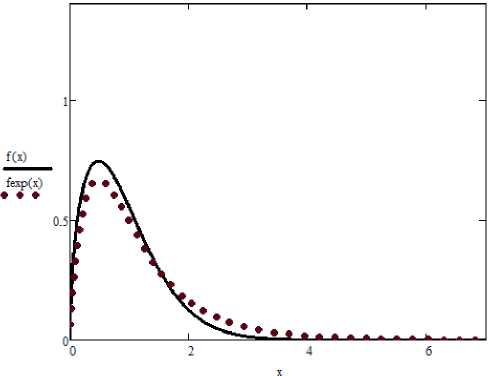
S,=0,64; я =3,318; S3 = -3,885 и a, = 0,89; a2 = 1,78; a3 = 2,68. Результат данной аппроксимации представлен на рис. 2. Абсолютная погрешность аппроксимации при этом есть H(x) = 0,061.
Рис. 2. Аппроксимация распределения Вейбулла: 2W И .fExp(x)
Плотность
^П
("^^ при
a
= 0,5 и
b
= 1,9 аппроксимируем суммой затухающих экспонент в виде
2п^ = Црте"“"
с параметрами;
M
=3,
pv
=0,042;
p,
=-0,612;
p3
= 1,752;
qx
= 0,32;
q2
= 0,65;
q3
= 0,97 .
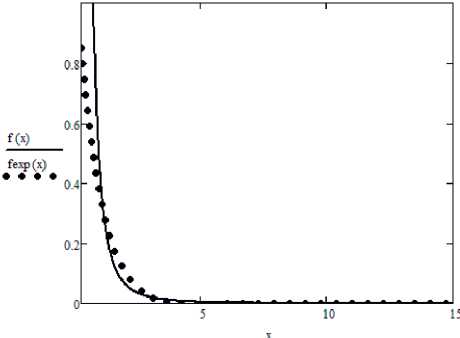
Результат аппроксимации представлен на рис. 3. Погрешность аппроксимации
7?(jt)
= 0,048 •
Рис.3. Аппроксимация распределения Парето:
/(-й И
КхДх')
Преобразование Лапласа для Ун (^0 будет м р иметь вид Fn^-Ъ— и, соответственно, м "z=1 q™ + 5 Осуществив простые, но достаточно объемные преобразования, для выражения Fn(-s)Fc^-l при выбранных значениях параметров аппроксимации распределений можно получить FnHFc^^ = =-----------------------------------------x
/(a, + s)(a2 + s)(a3
+ sXqv -s)(q2 -sXq3
-s)
x [s10 + s 9 £, (a, 9, 9, p, q^ +581\ (a, 9, 9, p, q, e-®0) + (14) + s\(a,9,9, p,q,e"sl°) + • • • s • r8 (a, 9, 9,p,q,e"iA") + +ЦоМр^, где kj, i = 1;2, и p, 7=1,2,...8 – коэффициенты, зависящие от параметров используемых распределений, причем эти коэффициенты зависят также от величины e ы°, что делает характеристическое уравнение выражения в квадратных скобках нелинейным и, соответственно, усложняет нахождение его корней. Например, численное значение коэффициента p определяется как r3 =O,5-l,5e"°'5$. Аналогично выглядят и остальные коэффициенты М = 1,2, ...8. Наличие множителя e °'5$ в каждом коэффициенте fj является следствием использования полиномиальной аппроксимации «восходящего» участка распределения Вейбулла. Так как структура всех коэффициентов r„j = \,2,..^ одинакова, используя разложение ' _ » zk экспоненты в ряд в виде ^-1>-^P не-k=o k\ трудно свести нелинейное уравнение (13) к линейному виду, решая которое численно, можно получить представление FhI-sXAsVV в виде V (5)
Fn(-Sxcx-^XX-
Такая возможность со-n c ^.(s)
храняется всегда при использовании полиномиальной аппроксимации «восходящего» участка любого распределения. + l,85s2 -2,2s+ 8,9 = 0. для можно ^(S) Обозначая корни характеристического уравнения через s*,i = 1, 2, 9, записать
^M
^ ^(s)
П^-^,’)
s4(aj +s)(a2 +s)(a,
+sXqt ~s)(q2 ~ХЯз ~s)
Выделяя в (15) по вышеизложенным условиям функции ^(5) и ^(s) и формируя O+(s) согласно (13), получаем значение среднего времени ожидания заявки в очереди
T
= 0,053 с (размерность
T
определяется размерностью величин
ak И Чт )•
Точность полученного решения определяется точностью аппроксимации распределений при решении уравнения Линдли спектральным методом. Метод селектирующих функций позволил заменить распределение Вейбулла ^ (*v) «сшитым» распределением
/с
(X) ’ состоящим из двух участков: «восходящий» участок (с положительным значением производной), который допускает простую аппроксимацию в виде полинома невысокой степени, и «нисходящий» участок (с отрицательным значением производной), аппроксимация которого осуществляется суммой затухающих экспонент с малым числом слагаемых в сумме. Такая аппроксимация обладает, как показано в работе, существенно меньшей погрешность по сравнению со случаем, когда используется единая аппроксимация распределения суммой затухающих экспонент. «Сшитое» распределение позволяет легко получить его преобразование Лапласа, что в конечном итоге сводит решение задачи к определению корней линейного алгебраического уравнения численным методом.
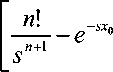
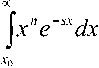
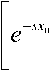
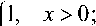
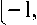
Список литературы Анализ СМО общего вида с использованием селектирующих функций
- Шелухин О.И., Тенякшев A.M., Осин А.В. Фрактальные процессы в телекоммуникациях. М.: Радиотехника, 2003. -480 с.
- Шелухин О.И., Осин А.В., Смольский С.М. Самоподобие и фракталы. Телекоммуникационные приложения. М.: Физматлит, 2008. -368 с.
- Kleinrock L. Queueing Systems: Vol. I, Theory. New York, Wiley Interscience, 1975. -417 p.
- Downey A. Lognormal and Pareto distributions in the Internet//Computer Communications. 2005. Vol. 28, No 7. -P. 790-801.
- Блатов И.А., Карташевский В.Г., Киреева Н.В. Чупахина Л.Р. Метод аппроксимации произвольной плотности распределения суммами экспонент//Вестник ВГУ. №2, 2013. -С. 53-57.
- Мищенко В.А. Метод селектирующих функций в нелинейных задачах контроля и управления. М.: Сов. радио, 1973. -184 с.
- Kartashevskii V.G., Kireeva N.V, Buranova M.A, Chupakhina L.R. Study of queuing system G/G/1 with an arbitrary distribution of time parameter system//2nd International Scientific-Practical Conference Problems of Infocommunications Science and Technology, PIC S and T 2015 -Conference Proceedings, 2015. -Р. 145-148.
- Караташевский В.Г., Киреева Н.В., Буранова М.А., Чупахина Л.Р. Моделирование и анализ системы массового обслуживания общего вида с произвольными распределениями временных параметров системы//Инфокоммуникационные системы. Т.13, №3, 2015. -С. 252-258 DOI: 10.18469/ikt.2015.13.3.03
- Агеев Д.В., Игнатенко А.А., Копылев А.Н. Методика определения параметров потоков на разных участках мультисервисной телекоммуникационной сети с учетом эффекта самоподобия//Проблемы телекоммуникаций. № 3 (5), 2011. -С. 18-37//URL: http://pt.journal.kh.ua/2011/3/1/113_ageyev_method.pdf
- Бахвалов Н.С., Жидков Н.П., Кобелков Г.Н. Численные методы. М.: Лаборатория базовых знаний, 2003. -632 с.


