Анализ собственных частот и форм колебаний жидкости в прямоугольной области в двухмерной задаче

• ¹    Самарский государственный университет

• ²    Самарский государственный аэрокосмический университет

Представлена математическая модель для расчета собственных частот и форм колебаний жидкости (газа) в сечении канала прямоугольной формы при формулировании краевых условий в общем виде. Рассмотрены частные случаи краевых условий: абсолютно жесткие стенки канала и упругие стенки канала. Приведены некоторые результаты моделирования на основе разработанной математической модели.

В настоящее время большое распространение получили численные методы анализа собственных частот и форм колебаний, что обусловлено высокой производительностью вычислительной техники. Однако наиболее общие закономерности изучаемых явлений позволяют выявить лишь аналитические ме- тоды, предоставляющие возможность получить решение задачи в общем виде. В настоящей работе предложена аналитическая модель для расчета собственных форм и частот колебаний жидкости в прямоугольном канале в двухмерной постановке.

Колебательное движение с малыми амплитудами в сжимаемой жидкости (или газе) в двухмерном случае описывается волновым уравнением [1]:

д 2ф  д 2ф _ 1 д 2ф дхг +ly^=С? "tF, где c – скорость звука в среде.

Геометрия области представлена на рис. 1. Жидкость ограничена прямоугольными границами с координатами x = ±а и y = ±b, краевые условия на которых записываются в общем виде:

Рис. 1. Геометрия решаемой задачи к± ф + k±ф = 0 при x = ±а, - b < y < b, дx

• i ± ^ф + 1 ± ф _ о при у _ ± ь, — а <  x <  а. ^д У

  ^ , (2)

  
  

где k ± ( У ) , k ± ( У ) , l ± ( x ) , l ± ( x ) ^- заданные величины, ф ( x,y,t ) - потенциал скорости, _те. V ,=^, V y =дф .

^x    д x       д у

Решение задачи будем искать в виде:

ф( x, y,t)=ф0 (x, у "ejrot, где ω – собственная частота системы;

ф ₀ ( x,y ) - собственная форма колебаний системы.

Воспользуемся одним из наиболее распространенных методов решения уравнений с частными производными – методом разделения переменных (методом Фурье) [2]. Собственные формы колебаний будем искать в виде произведения фо(x,y )= X (x )* Y (У ), где X(x) = а1 cos ax + а2 sin ax,(4)

Y(у) = b1 cos ву + b2 sin ву,(5)

a₁ , a₂ , b₁ , b₂ , α β - неизвестные искомые величины.

Из (4) и (5) получаем:

5 2X(x)_ дx  _-a X(x) •     (6)

⁸^ = ^{- e} Y ⁽ у ) •    (7)

Подставляя (3) - (7) в уравнение (1), после преобразований получим:

a + в = " 2 .        (8)

c

Таким образом, мы получили соотношение, связывающее собственную частоту колебаний ww с параметрами α и β , определяемыми собственными формами колебаний.

Вернемся к рассмотрению краевых условий. При этом рассмотрим только краевые условия на границе x = ± а , поскольку все преобразования для y = ± b будут аналогичны.

Краевые условия при x = ± а с учетом (4) можно переписать в виде:

AA

• a2 = -ai^" = -ai^~ (если AA * 0), (13) 1222

или

AA

• ^a i = ^{- a} 2 - = ^{- a} 2 - (если A 11 A 21 * 0 ). (14)

A11

Вернемся к выражению (12). Из него сле дует, что

A11A22 - A12A21 = 0.(15)

Подставим в (15) выражения (11). После преобразований получим:

tg (2M ) =

k 1 k + ^- k 1 k - k + k - M² + k - k + a²

^aM . (16)

k 1 ± ( + a 1 a sin aa + a 2 a cos aa ) +

+ k ± ( a 1 cos aa ± a ₂ sin aa ) = 0

Умножим (9) на a и обозначим M = a a .

Тогда после преобразований можно записать:

a 1 ( + k ± M sin M + k ± a cos M ) +

+ a ₂ ( k 1 ± M cos M ± k ₂ ± a sin M ) = 0 ^.

Последнюю систему уравнений можно переписать в виде:

Aua1 + A12a2 = 0, A21a1 + A22a2 = 0;

где

Из уравнения (16) можно найти неизвестную переменную α , определяющую распределение потенциала скорости в направлении x при собственных колебаниях жидкости в прямоугольной области. Уравнение (16) имеет бесчисленное множество решений, каждое из которых соответствует своей собственной форме колебаний. На рис. 2 графически показано нахождение решений уравнения (16). Аналитическое решение этого уравнения в общем случае не представляется возможным, поэтому для нахождения параметра α , соответствующего собственным формам колебаний, целесообразно использовать численные методы.

Проводя аналогичные преобразования для краевых условий y = ± b , можно получить:

An = - k + M sin M + k + a cos M, A 12 = k + M cos M + k 2 a sin M,

A 21 = k - MsinM + k - acosM, , ⁽¹¹⁾

A 22 = k - M cosM - k - asinM.

Система двух однородных уравнений (10) для двух неизвестных a₁ и a₂ имеет ненулевое решение если

A =

A 11

A 12

A 22

= 0

.

При этом одно из уравнений является следствием другого. Система сводится к одному уравнению и имеет бесчисленное множество решений, содержащихся в формуле:

tg ( 2N ) =

l - 1 + - 1 1 1 - l + 1 - N² + l - 1 + b²

bN

где N = p b .

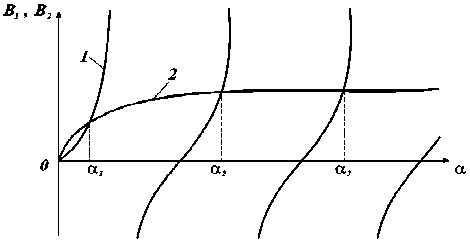
Рис. 2. Графическое нахождение решений уравнения (16):

1 - B 1 = tg(2M) ;

2 –

B 2 =

k l k 2 - k 1 k - k + k - M² + k - k + a²

aM

Таким образом, решив уравнения (16) и (17) при заданных k 1 , k 2 и l ± , l ± , можно найти собственные формы колебаний и поле потенциала скорости (с использованием выражений (3) и (4)), а после подстановки найденных значений α и β в (8) нетрудно определить соответствующую собственную частоту колебаний:

го = c ^O ² + в .

Собственные формы и частоты колебаний складываются из любой комбинации решений уравнений (16) и (17). Порядковый номер решения любого из этих уравнений определяет число узловых линий в соответствующем направлении.

Так, для первого решения уравнения (16) (тривиальное нулевое решение здесь и в дальнейшем рассматривать не будем) узловых линий в направлении оси y (вертикальных) нет, для следующего (второго) решения на поле распределения потенциала скорости появится одна узловая линия; для третьего решения – две узловые линии и т. д. Аналогичная ситуация будет наблюдаться и для решения уравнения (17). Однако в этом случае узловые линии будут располагаться горизонтально (в направлении оси x ).

Рассмотрим частные случаи задачи (1)-(2). В случае абсолютно жестких, полностью отражающих акустические волны стенок канала граничные условия можно записать в виде:

дф

= 0, при x = ±а, дx дф

= 0, при y = ±b. дУ вершенно аналогичны. Здесь также отметим, что X ( x ) и Y(У) будем искать с точностью до постоянного множителя. Для определения X(x) в форме (4) с точностью до постоянного множителя необходимо найти соотношение между a1 и a2 с использованием выражений (13) и (14). Выбор для использования выражений (13) или (14) определяется условием неравенства нулю произведения A12 A22 или A11 A21 . Из (13) для рассматриваемого частного случая, полагая k^ = k"- = 1, можно за- писать:

^П I ^{п п}

A 11 = —а аsin ( а а ) =~^ sin I

,

A 12 = а а cos ( а а ) =

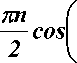
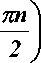
А                  ^{П П} • I ^{П П}

A 21 = а а sin ( а а ) = — sin I —

.            ( \ nn    I nn

A 22 = а а cos ( а а ) =    cos I

Тогда

12 22

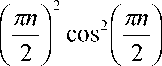
0, если n - нечетное ,

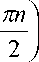
если n - четное ;

A 11 A 21

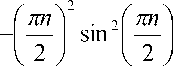
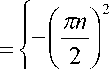
если n - нечетное ,

0, если n - четное.

Эти условия являются частным случаем

(2) при k ^ = k₂ = Г+ = l₂ = 0 . Тогда из (16) и (17) получаем:

πn    πm а = —, в = —,

2a ^,       2b ^,

чета

Таким образом, в случае четного n для рас- X ( x ) следует использовать выражение

(13); в случае нечетного n – выражение (14).

Более подробно рассмотрим случай чет-

где n и m – положительные целые числа.

Тогда выражение для определения соб-

ного

n .

A

ственных частот сист π е _c мы _n м 2 ожно _m з 2 аписать в виде: ^гопт =    1   5 + у .

2 a2   b2

I nn ^

■ tg — I и так как n - чет- к ² 7

Получим соотношения для собственных форм колебаний. При этом все математические преобразования рассмотрим для составляющей X ( x ) . Рассуждения для Y ( у ) со-

ное,

то

A11 = 0

A 12

.

Аналогично

A

πn

2"Т = tg УТ

A

I 2

и для рассматриваемого слу-

Таблица 1. Собственные частоты системы с абсолютно жесткими стенками

n	m	f , Гц	fANSYS , Гц	n	m	f , Гц	fANSYS , Гц
1	0	825	825	0	2	2200	2201
0	1	1100	1100	1	2	2350	2350
1	1	1375	1375	3	0	2475	2476
2	0	1650	1650	3	1	2708	2710
2	1	1983	1984	2	2	2750	2750
A                         тальном направлен чая четного n ”. — 0 . С учетом этого из Для проверки аде A 22                         аналитической мод выражения (13) получаем:                   с результатами рас a — о                   дом конечных эле! 2                       ного комплекса A Тогда составляющая X ( x ) с точностью по обеим моделям до постоянного множителя может быть запи- Результаты ра ООТТО Т> TITTTT^ сана в виде ных форм колебан π nx                     модельного случая X ( x ) — cos 2a , если n — четное.         Рассмотрим ей ной задачи – упруг Аналогично для случая нечетного n предположим, что о имеем: стины, выполненны π nx                 риала и имеющие a i — 0 , X ( x) — sin 2a ’если n - нечетное. краевые условия мс Итак, с учетом вышесказанного можно    д 4w ± р h д 2 w ± записать:                                                  4 ।          , д y    D д t cos    , если n четное,    ___ у. + p h___ у X ( x ) —J     2a                            д x4   D д t2 π nx sin    , если n нечетное. где w ( y,t ) - пр( канала ( x — ± a ), Проводя аналогичные преобразования       w ( x t ) - для Y ( y ) , получим:                                  y ,      ( нок канала ( y — ± cos y, если m четное,        д w x д w y Y ( y )—J , n ny                                 д t ■ д t -1 sin---, если m — нечетное. ^ 2b                              д w ± _ дф В качестве модельного примера рассмот-           д t — дx рим канал прямоугольного сечения размера ми 0,2 х 0,15 м и рассчитаем моды колеба-         д w ±    дф ний поперечного сечения при условии абсо-          я   — д лютного отражения акустических волн от          д t     д y стенок. В качестве рабочей среды примем воздух ( с — 330 м/с). Форму колебаний бу-       Р о - плотност дем характеризовать числом линий n в вер-       h – толщина тикальном направлении (параллельных оси       D – цилиндр y ) и числом узловых линий m в горизон- ны на изгиб:						ии (параллельных оси x ). кватности разработанной ели проводится сравнение чета этой же задачи метоментов на базе программ-SYS. Результаты расчета представлены в табл. 1. счета некоторых собствен-ий для рассматриваемого представлены на рис. 3. е один частный случай дан-ие стенки канала. При этом ни представляют собой пла-е из одного и того же мате-динаковую толщину. Тогда жно записать в виде [3]: -— D прих — ± a, P ±                 I ,(18) -— D при у — ± Ь, гиб вертикальных стенок огиб горизонтальных сте- b ), иброскорость стенок канала: , x —± a I ,(19) , y —± b ь материала стенок канала; стенок канала; ическая жесткость пласти-

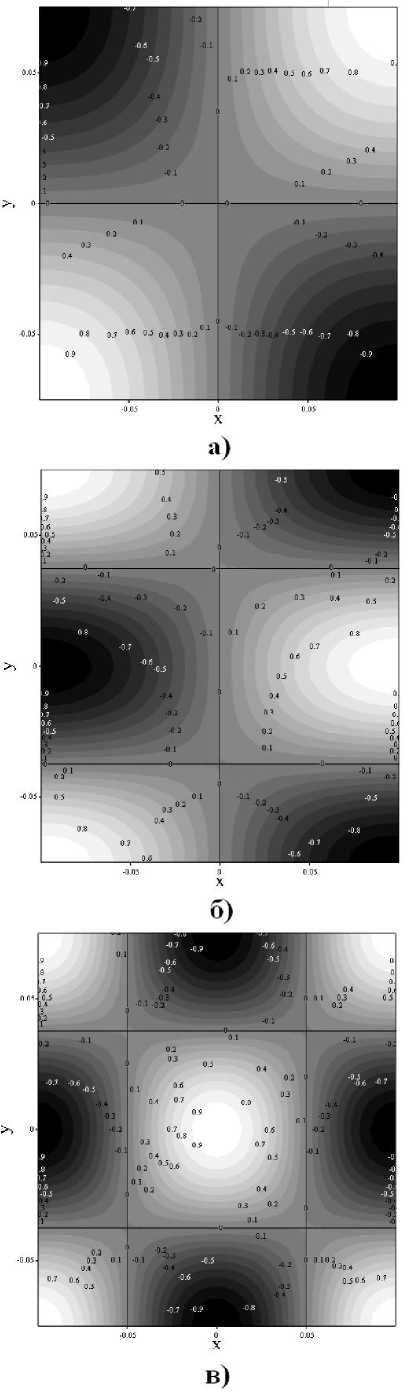
Рис. 3. Собственные формы колебаний исследуемой области (а=0,1; b=0,075 м) с абсолютно жесткими стенками: а – n=m=1; б – п=1; m=2; в – n=2; m=2;

––––– узловые линии

D = Eh³ 12 ( 1 — v² ) ^,

E – модуль упругости стенок канала;

v – коэффициент Пуассона;

p'

д ф

^{— p}^7 д t

x =± a

p ±

д ф — P

P д t

у =± b

[2],

ρ – плотность рабочей среды.

Рассмотрим преобразования краевых условий (18) для x = ± a . Преобразования краевых условий для у = ± b будут совершенно аналогичны. Продифференцируем первые два выражения из (18) по времени:

д 4 Гд<1 д У 4 1 д t J

₊ P o h ^{д 2} p w f

D д t² ( д t ,

p ^д 2 ф

D д t²

. (20)

x =± a

С учетом (19) выражение (20) можно переписать в виде:

д4 Г дфpoh д2 Гдф ду4 ( дx J + D дt2 I дx J д4 Г дф Y Poh д2 Гдф)

д у⁴ кд x J    D д t² кд x J

—

P ^д 2 ф

^D д t²

x =+ a

p ^

^D д t²

x =— a

Поскольку, как и прежде, мы ищем решение задачи в гармоническом виде:

—у = —ю ² ф 0 ( x,y ^j™ =—а ² ф . (22)

д t²

Подставляя (22) в (21), получим:

д ⁴ Г д ф )

I 1 + д у⁴ кд x J

P o h ^{д 2}

D дt2

д ф дx

ρω ²

-В" ^ф = 0

, x=+a

д⁴ Г д ф ^ P o h д² Г д ф ^ д у⁴ кд x J ⁺ D дt² кд x J

д2

Производную д t 2

разовать:

ρω ²

^{— ф} = °

Г!21 кдX J

x =— a

. (23)

можно преоб-

^{д 2} Г³^ 1 = ^{д 2} Г ^дФ ° ⁽ x,y ) e ™ 1 = _— ™ 2 ^д ф д t² кд x J д t² _ д x _ д x

.                             (24)

Подставляя (24) в (23) и учитывая, что решение ищется в форме (3) получим:

β ⁴

^

ρ ₀ h ω ²

D

д ф д x

ρω ²

-5-^ф = ^o

,

x =+ a

-

β

4   ρ ₀h ω ²

-

D

дф

д x

-

ρω ²

D

ф = 0

.

tg2M =

x =- a

2a X ^{4 P}^ ² ( kN⁴ -X ⁴ Q ² ) M

^P a X ⁴ Q ² ) - ( kN⁴ -X ⁴ Q ² ) 2 M²

P o h      7 ^V             ’

^“

Тогда, учитывая общую форму записи краевых условий (2):

(            2 А и-в - pih^, k-=-e - V , D           V              7

tg2N =

2 — P (kM4 h ρ0

^ )NQ2

ρb

k + = k - =- p^-

22 D

Аналогично:

V P o ^h

Ω2

А2

(kM4 - ^2)2 N2

.

.

Кроме того, с учетом принятых обозначений, выражение (8) можно преобразовать к виду:

l 1 = а

4   ρ ₀h ω ²

— -----

(

D

l -

-

α

-

, 2 A P o h to

D

X 2M2 + N2 =X2

2c^ I Q2

V c 7

l + = l - =

ρω ² D

Дополнительно обозначим

ε

Для записи уравнений в безразмерной форме, положим:

ωa      h2b

Q = — k = c0 ,     12a2 , где c0 – скорость звука в пластине [3]:

ρa ρ0 h .

В итоге получим систему трех нелинейных уравнений с тремя неизвестными: N , M и Ω :

откуда

2Ec0 = PoJl-V^) -

tg2M =

2e0X 4Q2 (kkN4