Анализ статических характеристик делителя потока непрямого регулирования

- синфазного функционирования [2] в установившемся режиме может быть оценена аналитическими = ( ), = (

[3, 4].

Ф(^) =

[^7У ^(^А^-1/1 ^~ ^(^р)’*^) + С_пр’КуУр\

Wp-^v))

XI

К

Рак- wp

где Кд_У — коэффициент динамической силы; Рак — сила давления аккумулятора; v — коэффициент [3];

пружины; К_у — коэффициент потерь на усилительном элементе; К_Р — характеристика чувсвитель-ного элемента; Qh— расход в системе; ср — ошибка синхронизации; v_P — скорость движения подвижного звена регулирующего элемента; х — перемещение подвижного звена усилительного элемента.

= ( ),        (

[5, считывать конструкции астатического регулятора и выбирать оптимальные конструктивные и эксплуа- тационные параметры двухдвигательной гидромеханической системы синхронно -синфазного функци онирования [3]. Полученные типичные статические характеристики делителя потока непрямого регу лирования представлены на рис. 1.

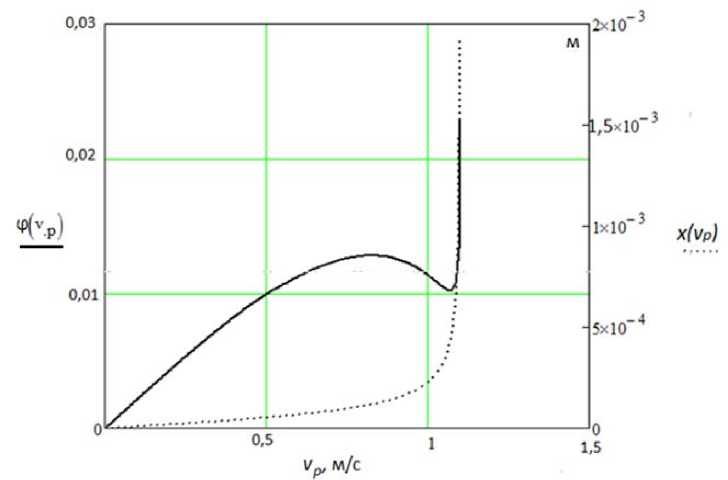
Рис. 1. Статические характеристики делителя потока

Особенностью представленных статических характеристик является наличие зоны неоднозначности и зоны насыщения в зависимости ср = /"(i^). Наличие зоны неоднозначности — нежелательный фактор, свидетельствующий о возможности возникновения автоколебаний в замкнутой системе, имеющей регулятор с такой характеристикой [7,8]. Поэтому конструктивно целесообразно ограничение скорости подвижного звена регулирующего элемента на уровне точки первого перегиба характеристики (фпор., v_pmax), что позволит получить характеристику регулятора типа пропорциональность с насыщением.

Для анализа работы астатического регулятора целесообразно в качестве основной зависимости использовать v_P = f^ (рис. 2). Зависимость x = f (i/_P) определена однозначно, и ее можно использовать как вспомогательную для нахождения % в характерных точках основной статической зависимости.

Форма основной статической зависимости и ее параметры: фпор, %no_P, v_Pmax, K_v = v_P/p — коэффициент усиления по скорости (добротность астатического регулятора) — могут существенно изменяться в зависимости от значений конструктивных и эксплуатационных характеристик.

На рис. 3 представлены основные статические зависимости делителя потока непрямого регулирования с усилительным элементом, имеющим нулевое перекрытие рабочих окон в нейтральном положении, для различной жесткости центрирующих пружин Gp (от 0 до 80 кН/м). Влияние параметра Gp сказывается на величине коэффициента усиления по скорости K_v. При увеличении жесткости центрирующих пружин уменьшается коэффициент усиления по скорости K_v, изменяются значения координат точки первого перегиба — характеристики фпор, Xnop, v_Pmax, причем фпор растет.

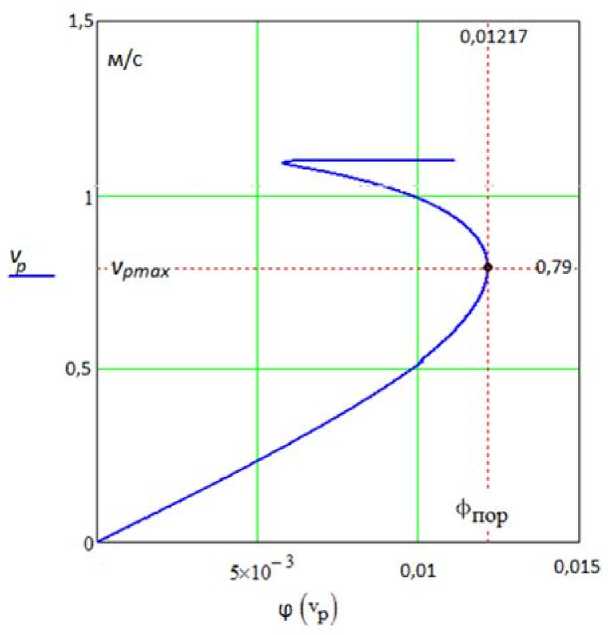
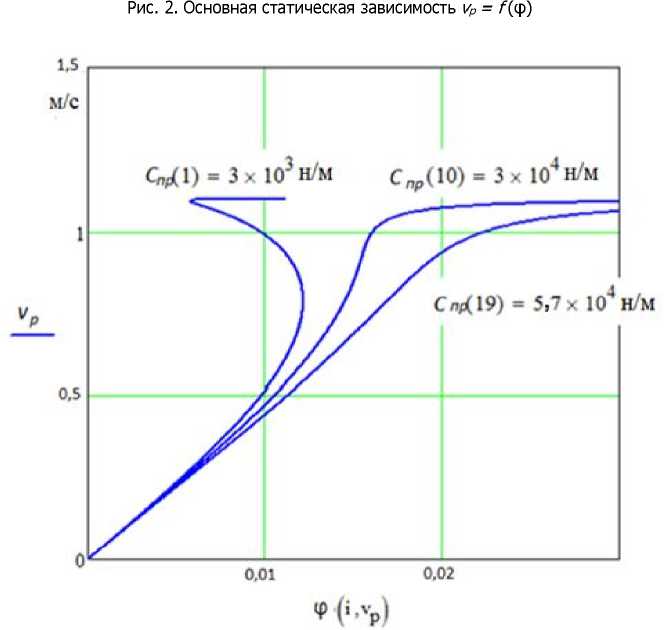
Рис. 3. Влияние Срна основную статическую зависимость

При жесткости Gp = 57 кН/м (рис. 3) форма характеристики изменяется и становится гладкой (убирается зона неоднозначности). Это свидетельствует о следующем. При определенной жесткости центрирующих пружин уменьшение осевой составляющей гидродинамических сил (после достижения ею максимума и при дальнейшем увеличении ошибки синхронизации ср) меньше приращения силы противодействия пружин. В балансе сил, действующих на подвижное звено усилительного элемента, силы противодействия пружин и осевая составляющая гидродинамических сил становятся равнозначными [1,9]. Расчет минимальной жесткости центрирующих пружин Gpmin, обеспечивающей гладкую статическую характеристику, производим по уравнению dp / dv_P = (1). Корни этого уравнения определяют экстремумы кривой v_P = корней уравнения можно утверждать, что кривая v_P =

Таким образом, можно определить минимальную жесткость центрирующих пружин Gpmin обеспечивающую гладкую статическую характеристику. Для этого следует по разработанной в пакете Mathcad программе выбрать значение коэффициента усиления по скорости /ч/для максимальной скорости регулятора v_P, которое будет удовлетворительным для конкретных условий эксплуатации. При этом ограничение по расходу подвижного звена усилительного элемента не требуется.

Результаты исследований статических зависимостей делителя потока непрямого регулирования с усилительным элементом, имеющим нулевое перекрытие рабочих окон в нейтральном положении, показали, что изменение значений диаметра регулирующего элемента dp (рис. 4) существенно влияет на значение коэффициента усиления по скорости Kv за счет изменения параметра скорости плунжера регулирующего элемента. При увеличении dp уменьшается Kv. Следовательно, dp должен иметь минимально допустимое значение.

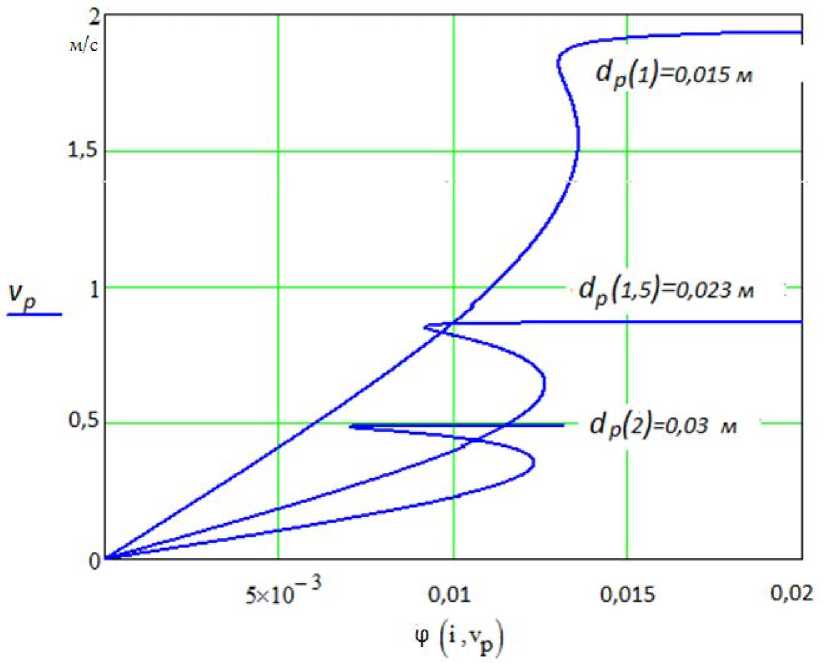
Рис. 4. Влияние d_P на основную статическую зависимость

Изменение диаметра усилительного элемента d_y3 незначительно влияет на величину коэффициента усиления по скорости Kv. При увеличении d_y3 возрастает фпор, уменьшается зона неоднозначности, v_Pmax остается практически неизменным. Таким образом, d_y3 должен иметь максимально допустимое значение.

Диаметр подвижного плунжера чувствительного элемента d₄₃we влияет на величину v_Pmax. При увеличении d₄₃ возрастает значение фпор и уменьшается K_v. При уменьшении d₄₃ уменьшается зона неоднозначности. Таким образом, d₄₃ должен иметь минимально допустимое значение.

При увеличении коэффициента демпфирования v уменьшается значение фпор и возрастает K_v , уменьшается зона неоднозначности. Коэффициент демпфирования и должен иметь максимально допустимое значение.

Давление аккумулятора рак значительно влияет на величину всех параметров основной статической зависимости фпор, айор, ц>тах, Kv. При увеличении давления аккумулятора рак уменьшается значение фпор и Vpmax, возрастает Kv, уменьшается зона неоднозначности. Давление аккумулятора рак должно иметь максимально допустимое значение.

Анализ характеристик для положительного перекрытия. Рассматривались основные статические зависимости делителя потока непрямого регулирования с усилительным элементом, имеющим положительное перекрытие рабочих окон в нейтральном положении А — как в зоне закрытых рабочих щелей (т. е. когда х < А), так и в зоне открытых щелей (когда х > А). Исследования производились по ранее полученным [1, 10] зависимостям (3), позволяющим учитывать радиальный зазор в золотниковой паре усилительного элемента 8.

ак шр

I/2

K_pQ^-K_fly^=-( Jx²+6²

Г К /          о 1\

6Т0°Юру( 1+2,94'10-J|2 )

'                       2 ^Vp

_   0,87Й^+52)3

- K_Kv_p - и/_р=0,

где top — площадь плунжера регулирующего элемента; у — удельный вес жидкости; Ь_у — периметр окна усилительного элемента; б — радиальный зазор в золотниковой паре; h — величина открытия щели; /— перекрытие рабочих окон усилительного элемента.

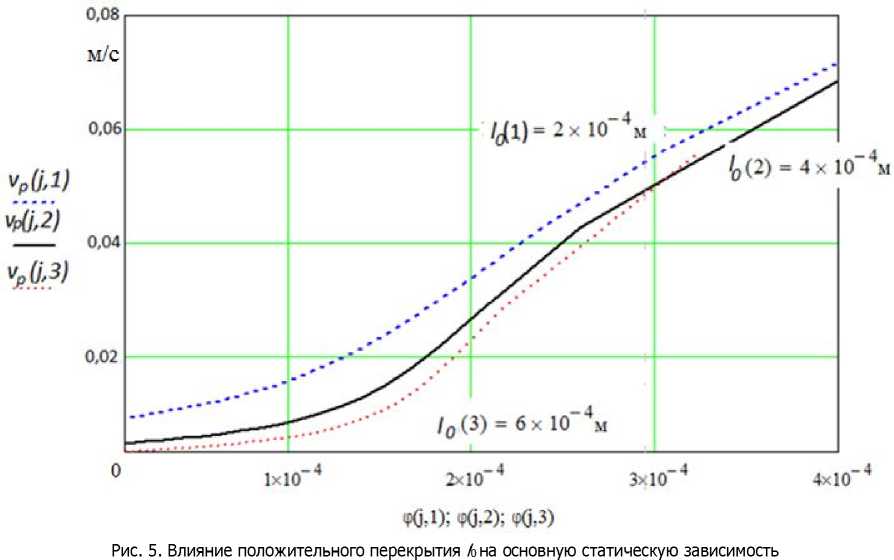
Результаты расчетов для зоны перекрытой щели (когда х <  А), приведены на рис. 5.

Из полученных кривых следует, что коэффициент усиления по скорости Kv незначительно зависит от величины начального перекрытия щели А, имеет тенденцию к постоянному возрастанию и при выходе к нулевому перекрытию практически совпадает со значениями Kv, полученными из модели для нулевого перекрытия.

Результаты расчетов по обобщенной модели (3) для зон перекрытой щели (когда х< А) и открытой щели (когда х> А) для А = 0,2; 0,4; 0,6 мм показывают, что величина начального перекрытия щели to незначительно влияет на форму и параметры основной статической зависимости. Форма основной статической зависимости идентична форме для нулевого перекрытия. Используемая для положительного перекрытия модель дает близкую к линейной зависимость с более существенными нелинейностями в переходных точках х = А и фпор, v_Pmax, Хпор (по сравнению с моделью, используемой для нулевого перекрытия).

Заключение. Проведен анализ статических характеристик делителя потока непрямого регулирования как астатического регулятора. Это позволило обосновать и получить оптимальную форму основной характеристики для различных конструктивных исполнений усилительного элемента. Указаны зависимости, позволяющие оценить работу астатического регулятора в двухдвигательной гидромеханической системе синхронно-синфазного функционирования в установившемся режиме. Определены методы и подходы, на основании которых проводятся расчет и выбор оптимальных конструктивных и эксплуатационных параметров указанного регулятора.