Анализ структуры математической модели привода полировального станка 3ПД-320А

Введение. Механизм полировального станка включает в себя две подсистемы, формирующие рабочие движения. Одной является привод опорного диска, а другой — привод, обеспечивающий «качательные движения притира». Оба привода созданы на основе электродвигателей постоянного тока, содержат ременную передачу и червячный редуктор. Наличие червячного редуктора позволяет предполагать незначительное влияние динамики процесса трения на динамические характеристики двигателя привода опорного диска. Привод качаний содержит четырехзвенный механизм, который характеризуется зависимостью момента инерции от угла поворота ведущего кривошипа.

Таким образом, представляет интерес определение устойчивого предельного цикла среди стационарных решений [1]. В этом случае необходимо оценить возможность разделения движений на «быстрые» и «медленные». Причиной такого действия, в первую очередь, является необходимость снижения порядка анализируемой системы путем получения вырожденной системы. Кроме того, как известно [1], «медленные» движения задают траекторию движения обобщенных координат, в нашем случае это движение детали по отношению к опорному диску, а «быстрые» движения — это смещение детали относительно траектории медленных движений.

При оценке поведения фрикционной системы необходимо учесть влияние динамических характеристик самого станка, причем в рассматриваемом случае технологическая машина обладает двумя приводами постоянного тока и кривошипно-ползунным механизмом привода качаний. Последнее означает, что система привода качаний является существенно нелинейной, с циклическим законом функционирования [2, 3].

Постановка задачи. Рассмотрим динамическую модель механизма станка 3ДП-320 (рис. 1). Он представляет собой систему с тремя обобщенными координатами. Две из них определяются наличием плавно регулируемых привода вращения опорного диска шпинделя (ϕ 1 ) и привода механизма качаний диска притира (ϕ 2 ). Третья степень свободы проявляется в относительном вращении диска притира относительно оси рычага механизма качаний. В приводах используются электродвигатели постоянного тока с независимым возбуждением, ременные передачи и червячные редукторы. Эти элементы привода одинаковы как по ϕ 1 , так и по ϕ 2 .

Рис. 1. Механизм привода шпинделя

Построим динамическую модель в виде графа и разделим ее на парциальные подсистемы (включающие по одному упругому, диссипативному и демпфирующему элементу) (рис. 2). Так как привод шпинделя и привод механизма качания частично совпадают, строим граф для общей части.

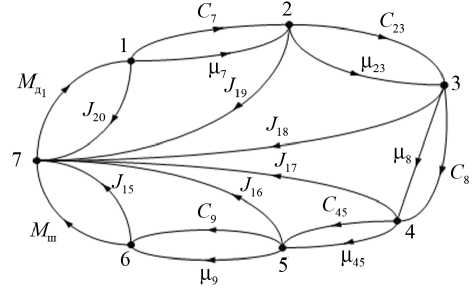
Рис. 2. Граф привода шпинделя

На основании матрицы инцидентности составляем систему уравнений привода шпинделя:

( J 20 + J 21 ) d ^ t ^ = ( M fv - M U — M 1 ( - о — ® 19 ) ) ,        dM U = C 1 ( ® 20 —® 19 ) ’

J 19 d^ ⁼ ( ^M 1 U - ^MU - M 2 ( ^Ю 19 ^-Ю 18 ) ) ’         dt^{2 =} C 2 ( ^Ю 19 ^-Ю 18 ) ’

J18   ,18 = (MU - MU - M3 (W18 - ГО17 )) ’       —--3- = C3 (to18 -ton ), dtdt

J17 , ,17 = ( MU - MU -M4 (^17 - ГО16 )) ’       ——7= = C4 (to17 - ГО16 ) ’ dtdt

J16 ,?6 = ( MU - MU - M5 (to16 - ГО15 )) ’       ——7— = C5 (to16 - ГО15 ) ’ dtdt

J 15 d ^PT = ( M U - M T^r ) . dt

Запишем систему уравнений привода опорного диска в матричном виде:

pUd = Ad • Ud + B, где Ud6 =(11  to20  to19  го18  го17  to16  MU  MU  MU  MU  MU)  — вектор неизвестных величин; B6 =(L 0 0 0 0 0 0 0 0 0 0)• U — вектор возмущающих воздействий; p — оператор Лапласа; Ad — собственная матрица системы.

- R - C 000000000 C         12        12       0     0     0       1       0     0     0     0 000   0000 Ad = I 20 + I 21     I 20 + I 21 I 20 + I 21                             I 20 + I 21 0       0      -12   X 0    0    -1   --1  0    0    0 I19       I19                          I19         I19 0        0        0    -13 ^^    0      0-1-  --1   0    0 I18    I18                            I18       I18 0       0       0     0   -14  14     0     0-1 - -1   0 I17    I17                            I17      I17 0       0       0     0    0  -15   1^    0    0-1  - X I17       I17                          I16      I16 0        C1        -C1      0     0     0       0       0     0     0     0 0         0        C2     - C2    0     0       0       0     0     0     0 0          0          0      C3   - C3    0       0       0     0     0     0 0         0         0       0    C4   - C4      0       0     0     0     0 _   0          0          0       0      0     C5       0       0      0      0      0 _ Проанализируем частотные свойства системы в целях выявления возможности упрощения математической модели.

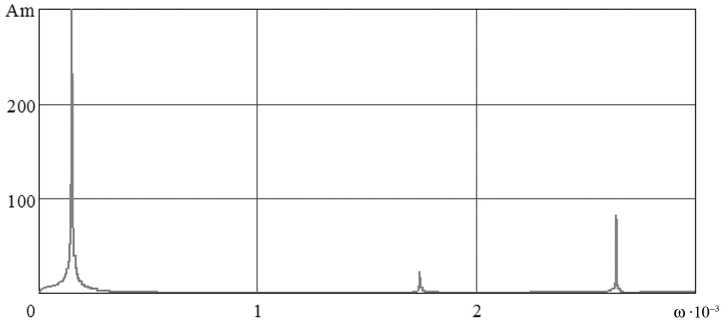
Рис. 3. Амплитудно-частотная характеристика привода опорного диска

Из приведенного графика (рис. 3) видно, что помимо основной гармоники, соответствующей основной резонансной частоте привода, есть также высокочастотные составляющие.

Проведем анализ возможности применения метода адиабатического приближения в целях упрощения математической модели.

Расчетные значения постоянных времени

Колебательная система	Ременная передача	Вал червяка	Червячное колесо	Опорный диск
T , с	5,647 - 10 - 4	2,821 - 10 -	3,494 - 10 - 5	7,645 - 10 - 3

Выводы. В связи с тем, что жесткость червячного редуктора на несколько порядков выше жесткости остальных элементов привода (см. таблицу), можно, используя метод адиабатического приближения, понизить порядок системы уравнений, считая жесткость редуктора бесконечно 650

большой величиной и приведя массы червяка и червячного колеса к предыдущему и последующему валам соответственно.