Анализ существующих колориметрических систем МКО

Эллиптичность поверхности цветового пространства

В начале 40 годов прошлого столетия Мак Адам опубликовал результаты экспериментов по определению порогов цветоразличения глазом человека [1]. Результаты опытов Мак Адама приведены на рисунке. Эти результаты были повторены Стайлсом [2] и Вышецки [3] и впоследствии повторены Мак Адамом. Все результаты хорошо согласуются между собой, и приведены в колориметрической системе МКО 1931 г. ( x,y ) и хорошо известны специалистам. На диаграмме МКО 1931 г. ( x,y ) результаты выглядят как эллипсы, причем размеры и ориентация эллипсов зависит от значения цветности.

Наличие эллипсов, а не кругов говорит о недостатках колориметрической системы МКО 1931 г. ( x,y ).

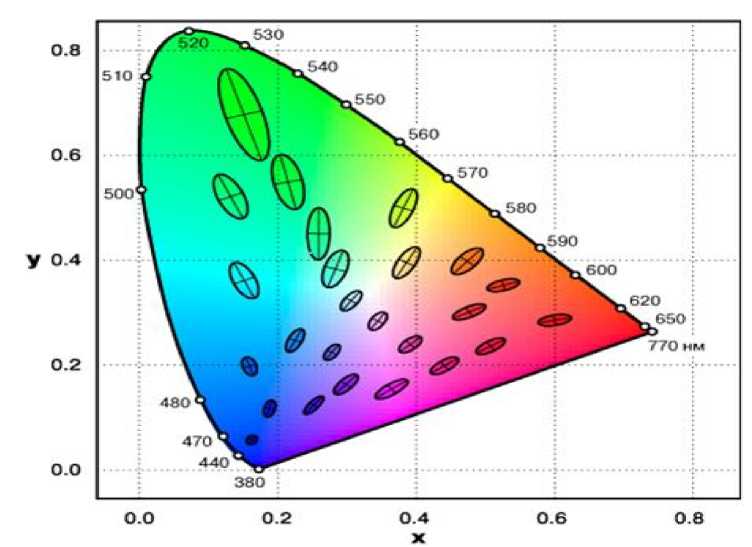
Пороги Мак Адама в системе координат x y (для наглядности величины эллипсов увеличены в 10 раз)

Впоследствии многие авторы разрабатывали так называемые равноконтрастные цветовые системы, к которым, к примеру, можно отнести: МКО 1960 г. (u,v), МКО 1976 г. (a*,b*) и другие. Но как, показали расчеты [4, стр. 294, таб. 7.2] ни одна существующая колориметрическая система не позволяет отразить на цветовой диаграмме вместо эллипсов Мак Адама – равновеликие окружности. В [4, 5] приведены результаты разработки квази-равнокотрастных цветовых пространств. Эти разработки опираются на ис- пользование тензорного аппарата, в частности метрического тензора.

Поверхность цветового пространства любой системы можно характеризовать эллиптичностью поверхности [6], определяемую в соответствии:

г = L mx

Lmin где L – максимальная ось эллипса, max

L – минимальная ось эллипса.

В таблице 1 приведены значения эллиптичности поверхности цветового пространства некоторых систем. В этой же таблице приведены значения порога цветоразличения для стандартного наблюдателя МКО и максимальное отношение площадей эллипсов Мак Адама.

Пересчет эллипсов Мак Адама в другие колориметрические системы, приведенных в таблице производился по известным формулам перехода [4] из одной колориметрической системы в другую.

Характеристики поверхности цветовых пространств.

Заключение

В таблице приведены значения эллиптичности цветовых поверхностей известных систем МКО. Как видно из этой таблицы, наибольшее значение эллиптичности присуще системе МКО 1931 г.(х,у), что является ее большим недостатком, хотя данная колориметрическая система является основной. Остальные системы были получены из этой системы, например МКО 60(u, v) была получена проективным путем, а системы МКО 76(u*, v*) и МКО LAB были получены путем математического нелинейного преобразования. И система (α, β), получена автором [2], путем логарифмически-экспонентального преобразования координат (x, y). Наименьшее значение эллиптичности из систем МКО можно считать МКО 60(u, v). Полученная автором Система (α, β) превзошла выше указанную по эллиптичности почти в 2 раза, но тем не ме- нее из таблицы видно, что ни одна цветовая поверхность не имеет значения ε=1, которое было бы идеально для поверхности цветового пространства.