АНАЛИЗ СУЩЕСТВУЮЩИХ МЕТОДОВ МОДЕЛИРОВАНИЯ И НОВЫЙ ПОДХОД К ФОРМАЛИЗАЦИИ КОНВЕРГЕНТНЫХ СИСТЕМ СВЯЗИ

Нарастание объемов передаваемого трафика в сетях связи увеличивается с каждым годом в виду того, что появляются различные приложения, которые критически зависят от высокой пропускной способности и качества каналов передачи данных. Примерами таких приложений являются: видео высокой (HD) и сверхвысокой четкости (4K, 8K), мультимедийные приложения с эффектом присутствия, дополненная реальность (AR), виртуальная реальность (VR) и смешанная реальность (MR) [1]. В самом ближайшем будущем ожидается, что количество «умных» абонентских устройств может достичь 8 млрд., большая часть из которых имеет возможность обеспечивать мобильный широкополосный доступ. Из них – количество различных мультимедийных приборов воспроизведения и демонстрации эффектов может превысить более 440 млн. для пользователей AR/VR, а более 40% автомобилей будут подключены к сети передачи данных с целью мониторинга состояния во время движения.

Так, по мере стандартизации узкополосного интернета вещей (NB-IoT), промышленного интернета вещей и полностью подключенных транспортных средств (Vehicle to Everything, V2X) мобильные сети сместили акцент с подключения людей с помощью расширенной мобильной широкополосной связи (Enhanced Mobile Broadband, eMBB) к подключению вещей с помощью сверхнадежных систем связи с малой задержкой (Ultra-Reliable Low-Latency Communication, URLLC) и потоковой межмашинной связи (Massive Machine Type of Communication, mMTC). Соответственно предполагается, что повсеместное коммерческое развертывание сетей 5G и 6G должно удовлетворить все эти потребности в предоставлении всеобъемлющего интернета (Internet of Everything, IoE), который станет основой для дальнейшего развития общества.

Основанием для внедрения таких сетей станет создание новой гибридной сети, которая будет конвергентной [2] и будет включать в себя как оптический сегмент транспортных линий связи и сегмент доставки сигналов до узлов точек доступа (малые ячейки базовых станций, макроячейки, удаленные радиоголовки, придорожные блоки и многое другое), так и сегмент радиосетей, включающий как наземные, так и неназемные системы связи. Это, соответственно, увеличивает количество и узлов точек доступа, а также

BY

число их вариаций, диверсифицируя параметры, которые должны быть включены в решения по управлению ресурсами вместе с динамическим развитием массовых коммуникаций. Также все это усложняется из-за того, что многомерные ресурсы таких сверхплотных сетей включают не только классические технические характеристики, такие как частота, мощность, время, пространство, но и энергию, вычисления и ресурсы хранения, что делает управление ресурсами ключевой научно-технической задачей при внедрении таких сетей следующего поколения. Все это свидетельствует о наличии тенденции к конвергенции телекоммуникационных сетей – объединению нескольких, бывших ранее раздельными, для формирования / предоставления изначально самых разных услуг в рамках единой комплексной услуги.

Это, в свою очередь, с учетом того, что конвергенция сетей неизбежна и именно конвергентная гибридная связь будет являться платформой для внедрения сетей 5 и 6 поколения, приведет к тому, что будут возникать технологические трудности и дифференциальная загруженность каких-либо одних технологий / сегментов сетей в противовес другим их типам / технологиям / сегментам. Отсюда очевидно, что работа различных частей такой объединенной сети будет отнюдь не оптимальной как по энергетическим и частотным затратам, так и по задействованию сетевой инфраструктуры и т.д. Последнее неизбежно будет затруднять модернизацию и масштабирование сегментов, а в ряде случаев, что не исключено, приводить к массовому выходу из строя перегруженного оборудования, и, в конечном итоге – просто к невозможности получения комплексной услуги, носящей системный характер, фактически сводя на нет достигнутые ранее результаты и понесенные затраты.

Поэтому уже сегодня требуется комплексное и систематизированное моделирование процессов в существующих различных системах связи с единых позиций. Возможная тому причина состоит том, что, несмотря на значительные различия телекоммуникационных технологий, имеет место их глубинное сходство – в структуре, в используемых ими аппаратно-программных средствах, а также в совокупности услуг, предоставляемых абонентам, и т.д. Тут надо подчеркнуть – именно совместное их формализованное описание в единой модели, которая должна учитывать еще и временные изменения, с последующей оптимизацией получаемых результатов. Отсюда целью настоящей статьи является выработка подхода к комплексному и формализованному описанию самых разных телекоммуникационных сетей/технологий в рамках единой модели, учитывающей также временной характер происходящих процессов. Последнее необходимо для того, чтобы, например, накапливать данные об условиях эксплуатации, запоминать результаты своих действий и используемые модели для той или иной окружающей среды1. На основе этих данных затем вносить коррективы в свою работу в зависимости от требуемой цели, и т.п. для организации эффективного управления канальными ресурсами в конвергентных сетях, на основе как стандартных методов, таких как резервирование канальных ресурсов, управление потоком трафика, объединение центров обработки данных, формирования приоритетных очередей и качества обслуживания (QоS), которые позволяют дифференцировать услуги, предоставляемые для различных видов трафика, так и использования различных инструментов, включая теорию оптимизации, теорию управления, теорию игр и теорию аукционов, которые будут распределять конечную пропускную способность в сети, в которой используются рыночные программные агенты, конкурирующие на децентрализованных рынках за покупку и продажу ресурсов или использование распределенного алгоритма совместного распределения скорости и мощности, который позволяет узлам сети оптимизировать свою производительность, даже в случае неэластичного трафика.

Анализ существующих подходов к аналитическому моделированию систем связи

Большой класс публикаций посвящен исследованию процессов приема-передачи сигналов в различных каналах связи с целью определения параметров работоспособности сетей – с изучением влияния помех и искажений [4–7], моделей телетрафика для определения характеристик надежности, устойчивости маршрутизации и подобных параметров [8–10]. При этом известны публикации, посвященные решению ком- промиссных задач по отношению к сетям связи, т.е. многокритериальной оптимизации с параметрами, противоречиво взаимосвязанными друг с другом, по методу Парето [11–14].

Также большое количество публикаций посвящено вопросам исследования управления ресурсами и внедрения конвергентных сетей. Таким образом, в работе [7] представлен обзор и описание различных технических параметров для конвергенции оптических и миллиметровых радиосетей с целью оптимизации их ресурсов с точки зрения автономного управления сетью, и предложена исследовательская программа, определяющая современные решения и необходимость смещения всех смежных вопросов в сторону создания усовершенствованного механизма управления ресурсами для сетей, выходящих за рамки 5G.

Так, например, в [11] рассматривается задача оптимизации системы связи, основанной на применении когнитивного радио, работающего в рамках IoT. Оптимизация проводится для обеспечения энергетической, спектральной эффективности и пропускной способности, с учетом отношения сигнал / помеха (SINR) и затухания. Разработан алгоритм оптимизации. Определяются параметры сетевой инфраструктуры: количество узлов, звеньев, каналов, потоков данных, пропускная способность канала/звена, и другие. В других статьях из этого класса решаются похожие задачи.

Однако следует заметить, что подобные модели ни в коей мере не позволяют, во-первых, взглянуть на различные типы систем связи комплексно, т.е. с единой позиции. Во-вторых, привнести в рассмотрение значимую временную зависимость, позволяющую формализовать с возможностью последующего анализа причинно-следственные связи в сложных системах, не говоря уже о необходимости в наглядной формализации одновременно и параллельно протекающих процессов. Учитывая значимость последнего именно для конвергентных сетей, для которых характерны разнородные, но параллельные процессы, а также задача выявления причинно-следственных связей, позволяющих выполнить анализ текущего состояния и возможность спрогнозировать состояние в будущем, возникает необходимость применения многомерного (2-х, 3-х мерного) моделирования. Перечисленный же выше класс моделей обязательно должен использоваться для получения количественных результатов, но может рассматриваться лишь как вспомогательный инструмент.

Одним из претендующих на указанные свойства является метод Сетей Петри [15–18], кото- рый предполагает построение графа состояний для моделируемого объекта (графы, Сети Петри, N-схемы) с последующей пошаговой нотацией процесса перехода объекта из одного своего состояния в другое. Метод хорошо зарекомендовал себя для задач параллельного программирования, дискретных динамических систем, в том числе для систем массового обслуживания, и т.д. В методе предполагается, что переход между состояниями осуществляется под воздействием заданных условий и возможен с различными вероятностями. Если выполняется условие отсутствия последействия, то процесс может быть представлен в виде цепи Маркова, что позволяет вероятности дальнейших переходов получить в результате решения системы уравнений Колмогорова [19; 20]. Могут рассматриваться также и процессы с последействием, где вероятности переходов также размещаются в матрицах [19].

Но согласно [15], метод Сетей Петри хорошо работает лишь для статических систем и совсем не отражает динамику функционирования моделируемой системы. Хотя в аппарате Петри и предусмотрено маркирование вершин графа, частично обеспечивающее различие «прошлых» переходов и состояний от «текущих», указанное не носит систематизированного характера и не может использоваться для формализации длительных процессов. К тому же в данном аппарате нет операций, позволяющих работать со всем комплексом параллельных процессов одновременно, а также отсутствует их совместное формализованное описание, что, несомненно, лишает модель наглядности и делает ее весьма громоздкой и запутанной при моделировании разнородных объектов, таких как составляющие части конвергентной сети.

Развитием схем Петри является более общий подход, предложенный Н.П. Бусленко [15; 21; 22], базирующийся на применении статистических моделирующих алгоритмов, понятии агрегативной системы и предполагающий построение операторной схемы общего вида (А-схемы). Метод изначально разрабатывался для нужд автоматизированного управления посредством автоматизации имитационного моделирования слоистых систем на ЭВМ. В отличие от классического графа Петри, Н.П. Бусленко при рассмотрении сложных систем выделяет два типа состояний:

• 1)    обычные (неособые) состояния, в которых система находится почти все время;

• 2)    особые состояния, характерные для системы в некоторые изолированные моменты времени, совпадающие, например, с моментами по-

• лучения входных и управляющих сигналов или выдачи выходного сигнала. В эти моменты состояние агрегата может изменяться скачкообразно, а между особыми состояниями изменение координат происходит плавно и непрерывно.

Агрегат представляет собой математическую схему общего вида, частным случаем которой являются функции алгебры логики, релейно-контактные схемы, конечные автоматы, динамические системы, описываемые дифференциальными уравнениями, и ряд других. Модель агрегата может быть использована как модель всей непрерывно-дискретной системы или ее элемента. В этом случае система представляется сетью агрегатов с фиксированными связями. В настоящее время метод широко применяется в объектно-ориентированном имитационном моделировании [23].

Однако с точки зрения рассматриваемой задачи – комплексного моделирования конвергентных сетей связи, метод Н.П. Бусленко не может быть эффективно применен в связи с тем, что здесь так же, как и в предыдущем случае, не удается привнести временное рассмотрение процесса. Предполагается, что система переходит между своими состояниями под воздействием случайных факторов, а не вследствие планомерного изменения. Последнее не отражает хода развития телекоммуникационных систем, на которые тоже влияют случайные факторы, но они, как правило, не оказывают существенного воздействия, выводящего систему на иную траекторию развития. Более значительные изменения достигаются в результате планомерного развития. К тому же, метод Н.П. Бусленко все же не обладает наглядностью при моделировании, отсутствует формализованная запись (модель) для всей системы в целом, а специализированные алгоритмы составляется раздельно после декомпозиции системы. Кроме того, методика фактически признается незаконченной [24], что подтверждается и самими авторами.

Подводя итог, заметим, что широко известный метод моделирования дискретных систем, предполагающий блуждание последних по своим состояниям, причем, как с дополнительным привлечением Марковских цепей и дискретных Марковских процессов, так и без них, не может быть эффективно использован для решаемой задачи.

Что вообще следует понимать под состоянием (комплексным!) для конвергентной сети связи? Реальное количество состояний такой системы очень велико, можно считать – приближается к бесконечности. Такие состояния априори сложно описать, не говоря уже об их развитии во времени. При этом надо еще уметь формализовать процесс воздействия факторов, влияющих на систему и ее изменение под их воздействием, также – во времени. И нужны не вероятности переходов, а формализация планомерных изменений под воздействием определяющих факторов. Требуется также наглядно моделировать параллельно идущие процессы. Необходимо заметить, что даже учесть все стороны влияния планомерно воздействующих факторов, приводящих к развитию составляющих конвергентной сети – это уже большая и практически значимая задача.

Кроме того, модели декомпозита не могут (по определению!) описывать всю систему в целом. Безусловно, такие модели и успешные приемы (в частности, по взаимной оптимизации их составляющих), обязательно должны использоваться для получения практически значимого результата, но уже в рамках основной общей модели.

Таким образом, можно считать, что в настоящее время отсутствует единый подход к формализованному описанию и моделированию конвергентной сети связи как единой взаимоувязанной системы. Это не позволяет адекватно спрогнозировать ее развитие, а также выполнить оптимизацию ее составляющих подсистем в условиях воздействия различных влияющих факторов.

Принцип формализации и моделирования конвергентных телекоммуникационных систем

Новый подход заключается в получении оператора преобразования, содержащего зависящие от времени характеристики как компоненты систем связи, составляющие конвергентную сеть, так и детерминированных и / или стохастических свойств факторов влияния. Наиболее близким является разработанный авторами ранее принцип моделирования многоканальных систем связи [25].

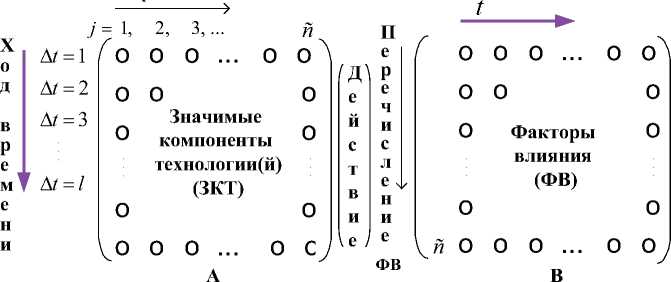
Для формализованного описания конвергентной сети (ФКС) предлагается использовать алгебраические объекты матричного типа подобно введенным в [25] (рисунок 1), в которых по строкам и столбцам представлены компоненты сети, либо влияющие факторы (назовем – функциональное свойство, его обсудим ниже, с номерами элементов, обозначенными через j∈ [1, n] на рисунке 1). Другое измерение – изменение этого функционального свойства со временем t (ход времени): т.е. при t1, t2 и т.д. Иными словами, столбец матрицы А – это фактически какой-то один функциональный элемент (функциональное свойство), значения которого могут отличаться в разные промежутки времени – для разных зна- чений £ . Окружностями для наглядности обозначены элементы матриц. Направления хода времени (увеличение £ ) и отсчета функциональных свойств (увеличение j) показаны условно стрелками. Причем направление хода времени может быть отражено не только по вертикали или горизонтали, а также по диагонали матрицы. Из сказанного следует, что измерения таких матриц принципиально не идентичны, поэтому при написании должно специальным образом обозначаться направление хода времени. В общем случае две матрицы одинаковой размерности с элементами, значения которых равны для одинаковых номеров строки и столбца, не являются тождественными, если не определено направление хода времени. Для несовпадающих направлений такие матрицы не равны. В этом смысле рассматриваемые здесь матрицы обладают векторным свойством.

Кроме того, процесс формализации предполагает выполнение алгебраических операций (специальных действий, сокращенно – Д [25]) над такими объектами матричного типа. Матрица С является результатом Действия. Для того, чтобы обозначить указанные действия применительно к рассматриваемой задаче, введем такое понятие, как Действие в ФКС. Так как в результате выполнения последних размерности2 рассматриваемых матриц могут меняться, то их тоже следует оговаривать. Так сокращенная запись операции, представленной на рисунке 1, может быть выражена следующим образом:

[ А (п) ^ ] . ( Д ) i [ В ( П ) ^ ] = *[ С ( т ) g ], либо

[ А (п) ^ ] i ( Д ) i [ В(п) ^ ] = *[ С ( М ) \ ] если гп = ^ .

Здесь и на рисунке 1 около знака равенства используется символ (*), что говорит о введенной операции – также по аналогии с [25] – равенства в ФКС.

Для направления изменения времени размерность каждой такой матрицы в общем случае может принимать бесконечное значение, равно как и в случае матрицы диагонального вида. Размерность же «функциональной» стороны конечна и определяется исходя из поставленной задачи. Так, например, если рассматривается формирование многоканального сигнала, то под функциональным свойством матрицы А можно понимать аппаратные пути для трибутарных (входных) пото- ков/сигналов, входящих в модуль STM-1, которых может быть 63 (в случае с потоками Е1 [26]). Под функциональным свойством матрицы В – сами 63 входных потока Е1, причем в матрице В они записаны с учетом всевозможных отклонений и искажений. Матрица С, получаемая в результате введенного Действия – произведения [25] для таких алгебраических объектов, тогда будет представлять собой многоканальный сигнал. В нашем примере – модуль STM-1. Но в отличие от широко известного представления (STM-1 из 63-х Е1 [26]), в данном случае в выходном сигнале будут отображены не только реальные свойства входных сигналов, но и неидеальности компонентов аппаратуры, преобразующих (мультиплексирующих) потоки Е1. Это позволяет определить возможность использования конкретного аппаратного средства (мультиплексора) с учетом особенностей его изготовления и условий эксплуатации, для формирования многоканального сигнала, на который можно затем наложить требование о соответствии стандартам (G.703, G.826 и подобным), в случае преобразования рассматриваемых входных сигналов с заданными искажениями. При несоответствии может решаться обратная задача, целью которой будет, например, нахождение точек деградации качества, приводящих к недопустимым искажениям мультиплексного (группового) сигнала.

Для корректного формирования выходного мультиплексного сигнала в формализованном виде дополнительно используется еще одно Действие – упрощение [25]. Оно позволяет превратить матрицу С в вектор-строку (либо вектор-столбец), над которыми далее вновь возможны подобные действия, так как все недиагональные элементы матрицы С равны нулю. Последнее имеет место в силу того, что используемое Действие между матрицами А и В – произведение [25], отличается от классического произведения матриц.

Обратимся теперь к процессу формализации предложенным методом конвергентных сетей связи. Последние при наиболее простом рассмотрении представляют собой совмещение в единую сеть многих телекоммуникационных технологий (WiFi, WiMAX, GPON и т.д.), работа которых нацелена на предоставление комплексных услуг, как это отмечалось во введении настоящей статьи. Поэтому под функциональным свойством матрицы А можно было бы понимать j-е технологии предоставления инфокоммуникационных услуг. Но ввиду того, что у подавляющего большинства последних в настоящее время имеет место общность по ряду факторов (функциональной струк- туре, формированию сигналов и т.д.), то целесообразно рассматривать не эти технологии целиком, а выделить некие общности и процесс формализации строить именно относительно них. То есть фактически рассматривать не сами технологии связи, а их компоненты (введем понятие – значимая компонента технологии, или ЗКТ).

Во-первых, это позволит избавиться от избыточности при моделировании, и, во-вторых, что принципиально даже важнее, такие общности (или ЗКТ) должны представлять, главным образом, технический, инженерный аспект, заложенный в основу построения той или иной инфо-коммуникационной технологии. Здесь следует заметить, что искомый при формализации процесс трансформирования таковых со временем касается, в первую очередь, инженерных положений, а описательная часть (названия, документирование, стандартизация и пр.) меняется уже в последнюю очередь.

Значимые компоненты технологии должны быть унифицированными, т.е. фактически одна и та же ЗКТ может применяться в различных реальных технологиях связи. Как именно разделить ту или иную технологию на ЗКТ, их количество, а также степень значимости с позиции сегодняшнего дня и ближайшего будущего, представляется условным и зависит от конкретно решаемой задачи и глубины анализа. В качестве рекомендации можно сказать, что целесообразно выбирать такие параметры, которые, с одной стороны, обеспечивали бы удобство и полноту описания исследуемой системы, а с другой – давали бы возможность получить достаточно простую математическую модель. При этом существенным обстоятельством представляется использование аналогий между явлениями и процессами различной природы. Отсутствие формальных правил исключает единственность выбора системы ЗКТ. Конкретный выбор может быть осущест-

Перечисление ЗКТ

влен только при рассмотрении сравнительно узких классов систем и с учетом их структуры и природы явлений, составляющих процесс функционирования. Возможно привлечение экспертных оценок, но в любом случае это является предметом отдельного исследования.

С точки зрения анализа конвергентных сетей на сегодня и ближайшее будущее, возможно, не столь актуально учитывать помехи и искажения в каналах ввиду существенного улучшения ситуации по отношению к временам становления систем связи, а понимать эволюцию систем, с точки зрения алгоритмов управления канальными ресурсами и показателей эффективности. Важно взаимное соотнесение параметров функционирования, таких как канальный ресурс, энергетическая, спектральная эффективности, пропускная способность и т.д., что в результате моделирования позволит понять преобладающие тенденции и направления развития инфокоммуникационных технологий.

Все сказанное выше распространяется и на Факторы Влияния (ФВ) – как по степени значимости в отношении конкретных ЗКТ и технологий связи, так и по распространенности, широте проявления, и т.д.

Здесь следует заметить, что непосредственно в модели по рисунку 1 было бы затруднительно использовать ЗКТ и ФВ в виде схемотехнического или словесного описания. Кроме того, они могут относиться к различным уровням сети, что практически исключает их непосредственное совместное сравнение / взаимодействие / оперирование. Поэтому при математическом моделировании целесообразно задаться некими приведенными параметрами: алгебраическими (счетными), либо логическими величинами (переменными). В качестве примера можно предложить: как ЗКТ, так и ФВ е [0,1], которые являются безразмерными величинами, либо описываются также приведенной (безразмерной) простой функциональной за-

ooo

~

m

oo

oo

.

.

.

om~ o

o

Эволуция системы

oo

.

.

.

o