Анализ свойств аномально диффузионных процессов на основе гребешковой модели

Аномальная диффузия присуща процессам в сложных неупорядоченных средах с меняющейся структурой, таких как, например, аморфные полупроводники, стекла, жидкие кристаллы, полимеры, протеины, перколяционные кластеры и самоподобные фрактальные среды, турбулентные потоки жидкости, газа и плазмы. Кинетика протекания процессов диффузион- ного переноса в таких системах часто отличается от классической, соответствующей нормальному закону распределения. Аномальный диффузионный перенос обычно обусловлен эффектами памяти среды, пространственной нелокальности и перемежаемости, имеет немарковскую стохастическую природу и поэтому не может быть описан классическими эволюционными уравнениями переноса.

Одним из эффективных и широко используемых подходов для описания процессов аномальной диффузии является использование аппарата интегродифференцирования дробного порядка. В этом случае уравнение процесса является интегродифференциальным уравнением, содержащим производные дробного порядка по временной и/или пространственным переменным. Следует заметить, что до настоящего времени отсутствует ясная физическая интерпретация производных дробного порядках [1]. Тем не менее было показано, что переход к производной дробного порядка по времени позволяет учитывать эффекты памяти системы [2].

Асимптотическое поведение решения обобщенного диффузионного уравнения дробного порядка

Для описания диффузии в пористых средах и установления аномального характера диффузии используем гребешковую модель. Она аналогична перколяции в пористых материалах и была введена для описания субдиффузии на перколяционных кластерах [3-6]. Структура модели состоит из проводящего канала (аналог скелета перколяционного кластера) и ребер, прикрепленных к оси (рис. 1).

y

x

Рис. 1. Гребешковая модель: ось и ребра, прикрепленные к оси структуры

Уравнение диффузии на структуре имеет вид:

г

д д t

V

е/Х д2      д2 )

• G ( x , y , t ) = 5 ( x ) 5 ( y ) 5 ( t ) .

- D _х 5 ( у ) -у — D 2~2 д x       о y J

Смещение в направлении x возможно только вдоль оси структуры, поэтому коэффициент диффузии D отличен от нуля при у = 0 и D = D,5 ( у ) .

Диффузия вдоль ребер носит обычный характер: D = D₂ .

G ( x , y , t ) - функция Грина для уравнения диффузии, в качестве начальных данных используется точечный источник 5 ( x ) 5 ( y ) 5 ( t ).

Будем рассматривать случайное блуждание вдоль оси структуры, которое и является аномальным.

Решаем уравнение с помощью преобразования Лапласа по времени и преобразования Фурье по координате х :

д

~

• ⁵ + D k ⁵ ( y )^{- D} 2 ^ GG G ( 5 , k , y ) = ⁵ ( y ) . o y

Решение одномерного уравнения (1) второго порядка по координате y найдем методом разделения переменных в виде

GG ( 5 , k , y ) = g ( 5 , k )exp( - 2| y |),                               (2)

где X - неизвестный параметр, а g ( 5 , k ) - неизвестная функция.

Подставляя выражение (2) в уравнение (1), получим уравнения [ 5 - D₂ X ²] G ( 5 , k , y ) = 0 и [ Dk ² + 2 X D ₂ ] 5 ( y ) g ( 5 , k , y ) = 5 ( y ), из которых находятся X и g ( 5 , k ) :

² DD 2 , g ( ⁵ ’ k )  2 D₂ 2 + Dk²

.

Преобразуем по Фурье решение (2) относительно координаты у :

G ( 5 , k , у ) =

(2D22 + Dk)(2 + kX)'

Соответственно получим уравнение диффузии для анизотропных случайных блужданий на гребешковой структуре: (2D22 + D1 k2)

[ 2k^

— + 22 к7

р ( 5 , k x , k_y ) = 0. Пренебрегая произведе-

нием k X k y и переходя в ( х, у, t )-представление, получим эффективное уравнение диффузии

д    D1   д2 д2

_ _ _ _ _

—

—

д 2

D 2. 2 р ( ⁵, ^k x , ^k y )

д у

= 0 •

Переходя обратно к прообразу и проинтегрировав его по переменным k_x , k_y , получим формальное решение уравнения дробного порядка по времени [7]:

e r              e - q ^{( 5} , ^т )

, 2

---^{5 (} t ^{- т} ) . (3)

G ( x , у , t ) = J J d5d т ----      —, где q ( 5 , т ) =

Найдем асимптотическое поведение решения уравнения дробного порядка вблизи начала координат [8] в двух случаях: при произвольных х , t и малых значениях у ; при произвольных у , t и малых значениях х. Будем исследовать асимптотическое поведение решения (3) методом перевала по переменной т . Вначале определим точки перевала:

1,2

‘ 0       ±.

x ²

4 D x s

y2

+ —<=

4Dy

•

Функция, стоящая в выражении для экспоненты, в перевальных точках равна:

f ( т 0 ) = - 2

x ²

4 D

s y ²

--1-- 5 + St .

• 4D xy

Далее вычислим интеграл по переменной 5 методом перевала. Уравнение для перевальной точки в результате принимает следующий вид:

y2      x2

12 5 2 —--+

4D4

yx

-у-

4 D

к У 7

5 +

x2   y2

--5+

4D4

xy

( 8 D X 1

•

Первый асимптотический предел – при произвольных x, t и малых значениях y

В случае малых значений координаты у будем искать решение для параметра s в виде разложения: 5 = 5 ₀ ( x ) + 5 , ( у ) .

Решение уравнения в исследуемом приближении и главном порядке 5 ₀ ( x ) имеет вид:

4 x ³

• ⁵ 0 = A 4/ ,

t ³

где А - постоянная величина.

y ²

Следующее приближение 5 , ( у ) описывается выражением 5] =----у . Таким образом, в по-^{1                                          1}   8 D y t ²

лученном приближении получаем выражение:

G ( x , у , t ) * exp <

—

Cx ³ y ²

_t ¹3      8 D y t

> ,

где константа

C =

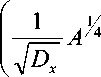
- A

J

Полученное асимптотическое решение имеет необычное, отличное от гауссова поведение по координате x . Видно, что плотность распределения по оси x приближается к виду

p ( y ) = exp( - x ^4/3 / A ) .

Второй асимптотический предел – при произвольных y и t и малых значениях x

В этом предельном случае s = s ₀ ( y ) + S j ( x ) + s, ( x , y ) . Тогда s ₀ ( y )

док по координате x равен нулю, в следующем приближении получим s

y

Первый поря-

x ⁴ D y 64 D x y ² .

И решение имеет вид:

G ( x , y , t )

e - p ⁽ x , y , t )

к .

4 n D_yt

p ( x , y , t ) =

4 D t ⁺ I y

x^D t y

64 D ² y ²

x J

Полученное решение в этом пределе имеет гауссово поведение по координате y и аппроксимируется соотношением p ( y ) = exp( - y ² / A ) .

Заключение

Получен обобщенный закон Фика в виде эффективного уравнения диффузии, имеющего дробный порядок по времени, для описания сильно анизотропной диффузии с различными временными зависимостями по отдельным координатам. Показано, что в асимптотических пределах больших времен плотность распределения вероятности имеет негауссов вид с различными законами убывания по координатам x и y .