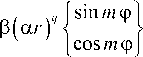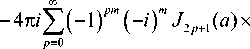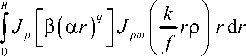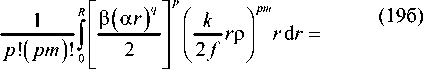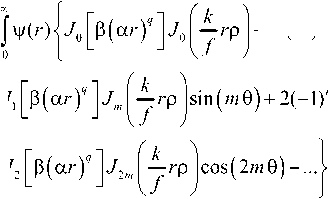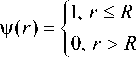Анализ свойств симметрии в фокальной области при наличии в фокусирующем элементе периодической угловой зависимости

Известно, что наличие различных аберраций в фокусирующей системе приводит к уширению, искажению и нарушению осевой симметрии фокального пятна [1]. Как правило, такое воздействие рассматривается как негативный фактор.

Однако, как было показано в работах [2,3], некоторые типы волновых аберраций позволяют уменьшить размеры центрального светового пятна в фокальной плоскости при острой фокусировке. В статье [2] были рассмотрены только первичные (осесимметричные) аберрации, а в работе [3] анализировались также аберрации с вихревой фазовой зависимостью на основе полиномов Цернике [1].

Полиномы Цернике имеют полиномиальную зависимость от радиуса и тригонометрическую (периодическую) угловую зависимость. В работах [4, 5] рассмотрены оптические элементы с периодическими угловыми изменениями. В статье [4] показано, что такой элемент формирует в фокусе нулевую интенсивность, а в работе [5] исследуются также без-дифракционные свойства сформированных пучков.

На основе разложения фазовой функции с косинусной угловой зависимостью по угловым гармоникам в работе [5] было показано, что функция пропускания вида exp {/'acos(m

В то же время известно [1,8,9], что аберрации нечётного порядка, такие как дисторсия и кома, проявляются в картинах с нечётной симметрией. В частности, в присутствии комы (т = 3) формируются распределения электромагнитного поля с симметри ей третьего порядка [10], напоминающие двумерные пучки Эйри [И].

Также произведение трёх одномерных функций Эйри, повёрнутых относительно друг друга на 120° и обладающих симметрией третьего порядка, преобразуется в спектральной плоскости в функцию, пропорциональную exp ^iar³ sin(3

В данной работе проведён анализ свойств симметрии распределения электромагнитного поля в фокальной области при наличии в фазе фокусирующего оптического элемента периодической угловой зависимости вида зш(тф) или соз(тф). На основе такой фазовой зависимости можно описать большинство волновых аберраций, которые, в свою очередь, могут быть представлены [13] через разложение по базису Цернике [ 1 ].

Аналитически показано, что при нечётных значениях т фокальное распределение будет действительной функцией, то есть фаза будет принимать только два значения — Ойл. Получены аналитические оценки для центральной части фокального распределения электромагнитного поля при использовании во входной плоскости круглой апертуры.

Численное моделирование подтверждает аналитические выкладки. Численно показано, что изменение радиальных параметров позволяет менять конфигурацию фокального распределения электромагнитного поля, но симметрия в центральной части в основном определяется чётностью углового параметра т.

1.    Преобразование Фурье от комплексной функции с периодической угловой зависимостью

Рассмотрим комплексное распределение с периодической угловой зависимостью общего вида:

Жф) = Y(r)exp

где ф(г) - некоторая осесимметричная функция, т -целое, q - положительное действительное, а, Р - действительные параметры (а имеет размерность мм ).

Заметим, что различные комбинации функций sin (тиср) и соз(отф) в фазовой функции (1) можно представить как произведение функций вида (1).

На основе комплексного распределения (1) можно описать большинство волновых аберраций, которые, в свою очередь, могут быть представлены [13] через разложение по базису Цернике [ 1 ].

Выберем для определённости в (1) зт(/иф). Если взять cos (/иф), то результаты будут аналогичными.

Пространственный Фурье-спектр для функции (1) записывается следующим образом:

F(p,6) =

Рассмотрим более общий случай: т - целое. Разложим первую экспоненту в (3):

ехр(-/я sin/иф) =

х

= J0(a) + 2^J2p(a)cos^2pm^-

X

"2'X    («) sin ((2р +1) т ф).

/=0

В (8) были использованы соотношения [14]:

□С'

cos(zsin t) = J_ti(z) + 2^ J_2p (-) cos(2pt^,

(9а)

sin

z^exp(zV)f z J? Г -о/ v =--—--J J exp^-zP(ar)

sin m ф x

Далее для вычисления интеграла (3) можно пользоваться известными соотношениями:

вос-

xexp

— 1

/у-грсо8(0-ф) бф>гбг,

(Ю)

где к = 2л / X - волновое число, /. - длина волны лазерного излучения,/-фокусное расстояние, (г,ф) и

= 2л(-гТ

(р,0) - полярные координаты во входной и выход

ной плоскостях соответственно.

Рассмотрим интеграл в фигурных скобках по углу:

Ф(р,0,г) = J exp -z'P(ar)’ sin/иф х

В результате получим:

ф(р,О;г) = 2к/о(а)Уо(6) +

ОО

+4^(-iym J^^J^^cos^pmQ)-

хехр

—z—"Гр cos(0 — ф) бф.

xJ(2p+nm(b)sm^2p + l)m6y

(И)

Для осевого распределения (р = 0) получим вы-

ражение, не зависящее от т\

Ф(0,0;г) =

ехр

■

Обозначим а = |3(агУ , b = кгр// .

При т = 1 в (3) сделаем преобразование: а8Шф + 6сО8(ф-0) =

= (а + б8т0)8тф + (бсо80)со8ф =

= ^(a + dsinO)2-^cosO)2 со8(ф-0') =

= Va²~v b^ + 2adsin0 cos (ф - 0'), где 0' = arctg^a +b sin 0) / b cos 0], тогда Ф(р,0;г) = 2лх

xj.

sinO .

Заметим, что выражение (11) при нечётных т будет действительным, т.к. коэффициенты в третьей сумме z(-z)'" = (—/)'" будут действительными при нечётных т.

Аналогично будет, если выбрать в (1) cos /иф :

exp (-/я cos/шр) =

X

= J₀ (a) + 2^ (-1)" J_lp (a) cos ( 2 pm ф) -

X

-7/У

Г2/,, |(r/)c°s((2/^ + 1)/7/<р),

где были использованы соотношения [14]: cos(zcos^) =

х

= 70 (z) + 2Х (-1/ J2p (z) cos (2 pt), sin (zcos/) =

(13а)

При выборе в (1) вместо simp (при т~Г) созф, формула (7) будет выглядеть аналогично с соответствующей заменой.

Tаким образом,

ехр (-ш cos /и<р) exp |^-zZ> cos (0 - ф)] dp =

= 2kJ0(«)J0(Z,) +

+ 4  (-ХУ^'Х Wi_pm (byos^pm^-  (14)

X

-4^(-iY^'4-iyj2p»x

V» =

PV^pF RP^.^2

---;----г—--------, Р > 0.

р'.^ртуУ(2.fy^m p(q + т) + 2

При нечётных т выражение (14) будет действи тельным.

Подставим (11) в (2):

-2/(-0"' х

х xj xj

г dr.

x

Выражение (15) можно переписать в следующем виде:

^(p,6) = -yexp(/V)x x{To(p)-2(4r,T1(p)sin(m0)+        (16)

+2(-1)”'Ч/2 (р) cos (2m 0)-...).

где

Т_р (р) = Jv^Vp ^(смУ р_р„, ^Jrp^ rdr. (17) Оценим приблизительно интегралы (17), положив

и считая

J0(z)«l-z2/4,

J„(z)^(z/2)''/h!.

Тогда

^(рЬ

= p0^P(ar)5p0^yrp^ rdr ~ гГ, P^ar)2" (fo-p)2!    _            (19а)

4 4Г у ^{Г =}

R²(рЯрогКр ррЛ²?

~ 2    8(^ + 1)     4/ Г

Как видно из выражений (19), основной вклад в центральную часть фокальной плоскости (при р —> 0) вносят слагаемые с низкими порядками р. Если ограничиться в (16) двумя первыми членами, то интенсивность в центральной части фокальной плоскости можно оценить следующими выражениями для чётных т:

НИ|2

yj [F^-^F^snFmO)]

(20а)

и для нечётных т:

НИГ = 4 [T((p) + 4vPl'(p)sin'(/»0)-

-4(-1)~То(р)Т,(р)8т(т0) , в которых первое слагаемое не зависит от угла, второе даёт 2m равномерно расположенных максимумов одинаковой величины (при sin(m 0) = ±1). Третье слагаемое присутствует только в случае нечётного т и корректирует эти максимумы: в зависимости от знака множителя при sin(mO) половина максимумов увеличивается, а другая половина уменьшается, и остаётся только т выраженных максимумов.

Таким образом, из выражений (20) видно, что симметрия в центральной части фокального распределения определяется чётностью т: для чётных т наблюдается симметрия порядка 2m, а для нечётных - т.

За счёт параметров Р, a, q и т можно варьировать значения коэффициентов в (20) и менять симметрию картины интенсивности в фокусе.

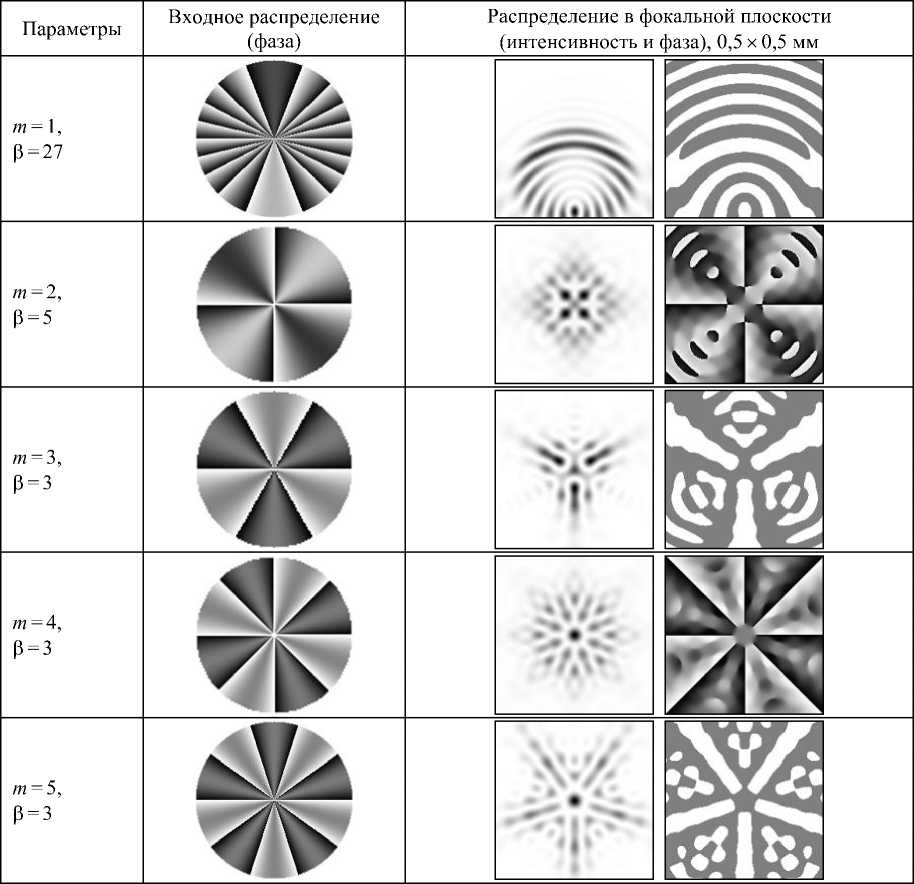
2.    Численное моделирование

При численном моделировании в формуле (2) использовались следующие параметры: длина волны излучения Х = 633 нм, фокусное расстояние f= 100 мм.

В табл. 1 приведены результаты при использовании в формуле (1) $1п(тф) с различными значениями т = 1,5 при <7 = 0 и различными значениями р, в качестве ф(г) выбрана круглая диафрагма радиусом 7?= 1 мм из выражения (17). Как было замечено в предыдущем разделе, при нечётных значениях т распределение в фокальной плоскости является действительной функцией, что соответствует бинарному типу фазы.

Также можно видеть, что для чётных т в центральной части фокального распределения наблюдается симметрия порядка 2т, а для нечётных - т.

В табл. 2 приведены результаты при использовании в формуле (1) 8т(тф) с т = 3 и различных значениях параметров а, Р и q, в качестве х|/(г) выбран гауссов пучок ехр(-г2 / о2) с радиусом перетяжки с = 0,5 мм. Как видно из приведённых результатов, изменение радиальных параметров позволяет менять конфигурацию фокального распределения, но симметрия в центральной части определяется значением углового параметра т.

Таблица 1. Результаты при различных значениях т и (3, q = 0, у/(Т) - круглая диафрагма

В табл. 3 приведены результаты при q = 0 и 0 = 5, но различных значениях т и ф (г).

Также рассмотрено использование вместо осесимметричной ф(г) более общей функции v(r), причём имеющей гармоническую зависимость от угла ехр (/7ф).

В первых 4 строках в качестве ф (г.ф) используются инвариантные к преобразованию Фурье моды Лагерра - Гаусса [14] различных порядков (и,/), в том числе имеющие вихревую зависимость ехр (//ф). Интересно, что наличие этой дополнительной зависимости от угла не столь существенно влияет на структуру фокального распределения, как периоди ческая функция рассматриваемого вида sin (;?гф). Если сравнить строки 1 и 3, то внесение фазовой вихревой зависимости в объектной плоскости приводит к появлению такой же зависимости в фокальной плоскости, не меняя основную структуру распределения (за исключением обнуления интенсивности в сингулярной точке).

При т = 1 действие похоже на внесение в фокусирующую систему аберрации типа комы, а при т = 3 - произведение трёх повёрнутых одномерных функций Эйри [12]. Хотя в последнем случае на самом деле имеет место произведение некоторых других одномерных функций.

В последних двух строках табл. 3 в качестве ф(г,<р) используются моды Бесселя J/(yr)exp(z7q>), Фурье-спектр которых выглядит как узкое кольцо с радиусом, пропорциональным у. Результаты моделирования показывают, что кольцевая фокальная структура бесселевых мод под влиянием периодического углового изменения в фокальной системе существенно преобразуется.

Заключение

В работе проведён анализ свойств симметрии распределения электромагнитного поля в фокальной области при фокусировке излучения с периодической фазовой угловой зависимостью вида sin(/zz

Аналитически показано, что при нечётных значениях т фокальное распределение электромагнитного поля будет действительной функцией. Таким образом, аналогично работе [12], можно формировать с помощью бинарных дифракционных оптических элементов в фокальной плоскости обычной сферической линзы фазовые распределения, соответствующие заданным типам аберраций. Такая возможность может быть полезна при острой фокусировке, когда наличие определённых волновых аберраций позволяет уменьшить размеры фокального пятна [2,3].

В частности, для светового излучения с круговой поляризацией таким фактором является присутствие комы (иг = 3), соответствующее двумерным суперпозициям пучков Эйри [11,12].

Численное моделирование подтверждает аналитические выкладки и показывает, что изменение радиальных параметров позволяет менять конфигурацию фокального распределения электромагнитного поля, но симметрия в центральной части в основном определяется значением углового параметра т; для чётных т в центральной части фокального распределения наблюдается симметрия порядка 2/и, а для нечётных - т. Причём внесённая фазовая вихревая зависимость вида ехр(;7<р) сохраняется в фокальной плоскости, но не так существенно влияет на структуру фокального распределения электромагнитного поля, как периодическая функция рассматриваемого вида sin(zwcp) .

Работа выполнена при поддержке Министерства образования и науки (ГК № 07.514.11.4055), грантов РФФИ 10-07-00109-а, 10-07-00438-а и гранта Президента РФ поддержки ведущих научных школ НШ-7414.2010.9.

Таблица 2. Результаты при различных значениях a, Р и q, т = 3, хурд - гауссов пучок

Таблица 3. Результаты при различных значениях параметров и вида у(г,ср) , q = 0