Анализ свойств смеси непараметрических оценок плотности вероятности многомерной случайной величины

Использование методов непараметрической статистики, основанных на оценках плотности вероятности типа Ро-зенблатта–Парзена [1; 2] является одним из активно развивающихся направлений моделирования систем при априорной неопределённости. Однако при усложнении условий исследования систем появляются методические и вычисли- тельные трудности применения традиционных непараметрических алгоритмов и моделей, что особенно наблюдается при обработке статистических данных большого объёма.

Перспективное направление «обхода» возникающих проблем состоит в применении принципов декомпозиции обучающих выборок по их объёму и использовании технологии параллельных вычислений.

Цель данной работы: на основе анализа асимптотических свойств непараметрической оценки смеси плотностей вероятности обосновать эффективность использования принципов декомпозиции при обработке боль- ших массивов статистических данных.

Непараметрическая оценка смеси плотности веро ятности и её свойства. Пусть выборка V = ( X , i = 1, n ) из n независимых н абл юдений k -мерной случайной величины x = ( x v , v = 1, к ) с плотностью вероятности p ( x ) . Вид p ( x ) априори неизвестен.

Разобьём выбор ку V на T групп наблюдений V j = ( x , i e I j ) , j = 1, T . Множество номеров наблюдений x в группе под номером j обозначим чере з I_j .

T

Причем U I j = I = ( i = 1, n ) . Количество n j = | l j| j =1

элементов в выборках Vj = (x' , i e Ij) одинаково и рав- n но n = T.

По каждой выборке V_j построим непараметрическую оценку плотности вероятности многомерной случайной величины x [1]:

f A pj (x)=—— ХПФ| -v^ I, j=1, T.  (1)

n П C v- ^e I j ^v =1 ^V c v )

v =1

В статистике (1) ядерные функции Ф ( u_v ) , удовлетворяют условиям нормированности, положительности и симметричности. Параметры ядерных функций c_v = c v ( n ) убывают с ростом n .

Пусть интервалы изменения значений компонент xv вектора x одинаковы. В этих условиях появляется возможность полагать, что значения коэффициентов cv непараметрических оценок плотностей вероятности pj (x), j = 1, T одинаковы и равны с. Тогда непараметрическая оценка (1) плотности вероятности принимает вид f _ „' A pj-(x) =     ЕПф| I, j = 1,T .     (2)

ⁿ c i e I j v =1 V c 7

В качестве приближения p ( x ) по статистической выборке V будем использовать смесь непараметрических оценок плотности вероятности типа

1T p (x ) = ^E pj-(x).               (3)

T j =1

Статистика (3) допускает использование технологии параллельных вычислений при оценивании плотности вероятности в условиях больших выборок.

Асимптотические свойства p ( x ) определяются следующим утверждением.

Теорема . Пусть p ( x ) и первые две ее производные по каждой компоненте x_v , v = 1, к ограничены и непрерывны; ядерные функции Ф ( u_v ) удовлетворяют условиям

ф ( U v ) = Ф ( _ U v ) , 0 < ^ф( U v ) <” ,

|Ф( uv ) duv = 1, j u2 Ф( uv ) duv = 1, j uvm Ф(uv) duv <да, 0 < m <да; v = 1, к , последовательности c = c (n) коэффициентов размытости ядерных функций непараметрических оценок плотности вероятности (1) таковы, что при n ^ да значения c ^ 0 , а nck ^ да .

Тогда при конечных значениях T непараметрическая оценка (3) плотности вероятности p ( x ) обладает свойством асимптотической несмещённости и состоятельности.

Здесь и далее бесконечные пределы интегрирования опускаются.

Доказательство .

По определению имеем

₁ T ₁ T ₁

M ⁽ p ^{( x} ) ) = уХ M ⁽ p j^{( x} ) ) = yZ    ^х

T j=1                   T j=1 nc f x _ x' A

XZfK ТПФ|  ---L I p(x1,K, xk ) dx1 K dxk = i eIj         v=1 V c )

=7 J K Jii < x c           v =1 V

k

= J к Jn ° ⁽ u v ) p ^{( X} 1

v =1

c

— I p ^{( -} 1 , K , ^- k ) ^dt 1 к dt_k =

cu₁,к, x_k - cu_k ) du 1 к du_k ,

где M - знак математического ожидания. При выполнении преобразований учит ывае тся, что элементы статистических выборок V j , j = 1, Т являются значениями одной и той же случайной величины t с плотностью вероятности p ( - ₁ , к , t_k ).

Разложим p(x1 -cu1 ,к, xk -cuk) в ряд Тейлора в точке x = x1, к, xk и ограничиваясь первыми двумя членами ряда, имеем c2

W 1 = ^M ( p ^{( x} ) ^- p ^{( x} ) ) ~ —Z p V ( ^x ) ,      ⁽⁴⁾

² v =1

где p V ²* ( x ) - вторая производная плотности вероятности p ( x ) по компоненте x_v .

Отсюда, из условия c ^ 0 при n ^ да следует свойство асимптотической несмещенности смеси непараметрических оценок плотности вероятности (3).

Для доказательства сходимости p ( x ) в среднеквадратическом рассмотрим выражение

^M J к J ( p ^{( x} ) ^{- p ( x} ) ) ^{2 dx} 1 к ^dx k =

-12

1 Л/

= ^M J K f - ^ ( Р ( ^Х ) — P j^{( Х} ) ) ^dX 1 K ^dx k =

T

= M sj - J ( p ⁽ x ) ^- P j (x ) ) ² dx к dx k ⁺

^-       L j =1

TT

⁺EEJ k J ( p ^{( x} ) ^{- р}д ^x ) ) ( p ^{( x} ) ^- д ^{( x} ) ) dx к dx k j =1 t =1 t * j

. (5)

Найдем асимптотическое выражение составляющих второй части выражения (5):

^M J к J ( p ⁽ x ) - p j ⁽ x ) ) ( p ⁽ x ) - Р, ⁽ x ) ) ^dx 1 к ^dx k =

= J к J p ² ( x ) dx1 к. dx k -

-M J к J pt (x) p (x) dx1 к dxk - M x xJ... J pj ( x) p (x) dx1 к dxk + M J к J pj (x) pt (x) dx1 к dxk . (6) Преобразуем его последнее слагаемое

M J к J pj ( x ) p>_t ( x ) dx к. dxk =

= J к J M ( p j ( x ) ) M ( p_t ( x ) ) dx 1 к dx k , которое при достаточно большом объеме статистических данных с учётом выражения (4) представляется в виде Г          c ²

J к J I p ( ^x ) ⁺ лг£ p V ( ^x ) I dx к^dx k .     ⁽⁷⁾

V           ² v =1           )

Заметим, что асимптотическое выражение статистики типа

M J к J p_t ( x ) p ( x ) dX 1 к dx k соответствует

Jк J| p ( x ) + c- ^ pV2)( x ) । p ( x ) dx1 к dxk .

V          2 v=1

Подставляя выражения (7), (8) в (6), после несложных преобразований получим

M J к J( p (x)- pj( x))( p (x)- p- (x)) dx1 к dxk ~ r4        ( k            A2,^4

~тJкJ|ZpV2)(x)I dx1 кdxk =tB.

4 V v=1         )

В работе В. А. Епанечникова [2] получено асимптотическое выражение для среднеквадратического отклонения непараметрической оценки плотности вероятности от p ( x ), составляющих первую часть выражения (5):

^M J к J⁽ p ⁽ x ) - p j ( x ) ) dx 1 к dx_k ~

k nJ» ‘ (u. ) du. „4

~ ^v"   _ , -----+ -B           (10)

n c         4

С учётом (9), (10) выражение (5) при достаточно больших значений n представляется в виде k

, ,      _   2           Ш^ф ( и . ) du . c .

^M /к] ( p ⁽ x ) ^- p ⁽ x )) dx ' ^ ^dx k ~ ^V " '       k ----- ⁺ V ^В . (11)

^{J J}                              -nc 4

Нетрудно заметить, что в условиях c ^ 0 , nc^k ^ да при n ^ да оценка смеси плотностей вероятности (3) сходится в среднеквадратическом к p ( x ) , а с учетом свойства ее асимптотической несмещенности является состоятельной.

При Т = 1 и n = n полученный результат (11) совпадает с утверждением теоремы В. А. Епанечникова [2], что подтверждает корректность выполненных преобразований.

Анализ аппроксимационных свойств статистики p(x). Для анализа эффективности непараметрической оценки смеси плотностей вероятности (3) и оценки плотности вероятности типа Розенблатта-Парзена nk       i p (x ) = тт Sn®!^ j     (12)

ⁿc 1 =1 v =1 V c )

рассмотрим отношение соответствующих им асимптотических выражений среднеквадратических отклонений при оптимальных значениях коэффициентов размытости ядерных функций.

Определим минимальное значение W2 выражения (11) при оптимальных значениях c коэффициентов размытости непараметрических оценок pj (x) составляющих смеси плотностей вероятности. В принятых допущениях значение

*

c

k ii J 0 ² ( u . ) du .

v=1_________________________ nB

.

Тогда

W 2 =

k nJ»2 (u.) du.

Bk

/( k +4 )

n

^{4 +} Tk . (1³)

4 Tk ^{/( k + 4 )}

Если k = 1, то W ₂ совпадает с минимальным асимптотическим выражением среднеквадратического отклонения для смеси непараметрических оценок плотностей вероятности, полученного в работе [3].

При T = 1 и n = n выражение (13) соответствует минимальному асимптотическому выражению W 2 , среднеквадратического отклонения для непараметрической оценки плотности вероятности (12) типа Розенблатта– Парзена [2].

Отсюда, после несложных преобразований, получим

R 2

W =   4 + Tk

W ‘ ( 4 + k ) T^^{k + 4 )}

гомерной случайной величины обоснована возможность декомпозиции исходных статистических данных при синтезе непараметрических статистик в условиях больших выборок. Исследуемая статистика по сравнению с традиционной непараметрической оценкой плотности вероятности типа Розенблатта–Парзена имеет значительно меньшую дисперсию и позволяет использовать технологию параллельных вычислений.

По аналогии вычислим отношение минимальных зна-

чений главных дисперсионных составляющих статистик

p (x) и p (x):

W 3 =

k

Tk /(k+4)

(_ ^4 П/Ф ( uv ) duv

v =1 _________________________

n

/: ^k +4 )

Их отношение имеет вид

R 3 =

W 3

W 3

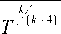
Bk

а

Нетрудно убедиться, что отношение асимптотических выражений смещений W , W ^ анализируемых оценок плотности вероятности p ( x ) и p ( x ) при оптимальных коэффициентах размытости ядерных функций соот-

ветствует значению

R = W = t Уk ^{+ 4 ) 1} W

С ростом количества T составляющих смеси непараметрических оценок плотности вероятности наблюдается увеличение значений отношений R ₂ > 1 (см. рисунок, часть а ), R ₁ > 1 (см. рисунок, часть б ). Отм е ченное ухудшение аппроксимационных свойств смеси p ( x ) по сравнению с традиционной непараметрической оценкой плотности вероятности p ( x ) (12) объясняется снижением объёмов выборок, используемых при оценивании составляющих p ( x ) . Данная тенденция особенно характерна для малых размерностей k случайной величины x . При усложнении условий оценивания плотности вероятности с ростом k эффективность непараметрических оценок p ( x ) и p ( x ) снижается. Соответствующие им критерии W ₂, W 2 и W , W ' становятся соизмеримыми, что проявляется в снижении значений их отношений R ₂ и R ₁ .

Предлагаемая смесь p ( x ) оценок плотности вероятности обладает меньшей дисперсией по сравнению с непараметрической оценкой p ( x ) , что обусловлено её структурой, так как синтез статистики p ( x ) осуществляется на основе усредняющего оператора (см. рисунок, часть в ). Причём с увеличением количест в а T составляющих смеси непараметрических оценок p ( x ) плотности вероятности и размерности k случайной величины её преимущество возрастает.

На основе анализа асимптотических свойств смеси

Зависимости отношений: R ₂ ( а ), R ₁ ( б ), R ₃ ( в )

от размерности к случайной величины x = ( x_v , v = 1, k ) и количества T = 1–10 (кривые 1, …, 10)

составляющих смеси непараметрических оценок плотности вероятности p (x) (3)

непараметрических оценок плотности вероятности мно-