Анализ технологических остаточных напряжений, возникающих в многослойных композитных панелях с несимметричной структурой пакета композита по толщине

влияние и на несущую способность элементов конструкции при действии на них внешнего нагружения. Для оценки несущей способности слоистых элементов конструкции под воздействием суммарных остаточных напряжений { o f ^, H } в каждом слое необходимо знать характеристики прочности слоев, из которых состоит элемент.

Прочностью слоя волокнистого композита при нагружении считается то предельное напряжение, которое вызывает разрушение (разделение) слоя или при котором достигается его предел пропорциональности.

В отличие от металлов волокнистый композит, как известно, характеризуется пятью компонентами прочности: при растяжении вдоль воло-+ кон <у1 , при сжатии вдоль волокон <71 , при растяжении поперек волокон ^2+ , при сжатии поперек волокон σ2- , прочностью на сдвиг τ12 .

Расчет на прочность слоистых композитов заключается в последовательной оценке прочности составляющих его слоев, находящихся в плоском напряженном состоянии. При этом используются различные феноменологические теории и критерии прочности, которые должны в той или иной степени учитывать особенности поведения этих материалов.

В рамках анизотропной модели, пользуясь технической теорией тонких пластинок, рассмотрим расчет многослойной панели, обладающей анизотропией вследствие несимметрии свойств структуры пакета по толщине и находящейся под действием температурного поля Т и технологического натяжения К_НВ .

Препреги предварительно натянуты, после отверждения натяжение снято. Так как структура слоистого элемента несимметрична, при последующей реализации гипотез о нормальном элементе в расчетной схеме теряется смысл сре- динной поверхности. Поэтому плоскость приведения, в которой располагаются координатные

оси, и, соответственно, начало отсчета координаты z в дальнейшем могут быть выбраны произвольно. С использованием гипотезы Кирхгофа, соотношений Коши, формул геометрических преобразований, а также закона Гука с учетом влияния температуры и формул преобразования напряжений при повороте осей [2, 4, 8] получим выражения для компонент состояния k -го слоя [5, 6].

( K )

Л ( K ) _     ^E 1          KK ) _Z)( K ) _Z)( K )..( K ).

• ^Q 11 "       ( _K ) ( _K ) ; Q 12 "  ^Q 21 "  ^Q 11 ^v 21 ;

• ^{1    - v} 12 ^v 21

_F ( K )                                  ⁽⁴⁾

( K )         E 2             ( K )      ( K )

^{Q 22} "l -_v( K V K )^{; Q 66} = ^ ¹² • 1 v 12 v 21

Преобразование для коэффициентов температурного расширения представлено в виде:

( K )

( K )

( K )

Q 11

Q 12

Q 16

р

L ' xy

Q 21

Q 22

-

Q 16

Q 66

- (K)

£ X + K X z ⁽ K ) - a i   AT - e h i

-(K)

£ ' + K y Z ⁽ ) - a 2   A T - e h 2

-(K)

Y P + K P z ⁽ K ) a 6 A T - £ h 6 xy xy

,(1)

^a 1

-

\a2 ^

^a 6

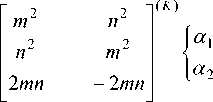
Для деформации натяжения имеем:

оо

^£ x ^£ x ⁺ K x

d и о

• z —----- dx

оо

^£ y ^£ ' ⁺ K y

5 Vо

• z —----- dy

d2 W

—2 • z;

d x ²

а2 w ay2 'z;

( K )

оо

< xy <  xy xy

_ d U о d V о    d ² W

• z 12z, dy   dx    dx dy

^£ H 1 ^- \£ h 2 >

^£ H 6

m m

" s n

2mn

ooo

где £ x , £ y , Y xy

-

деформации в плоскости приве-

дения, K x , K ' , K x _y - кривизны панели.

^{( K} )

-     { £ h } ^{( K} )

где m ^{( K} ) и n ^{( K} ) тригонометрические функции угла поворота осей координат (1, 2) связанных с “ k ”-ым слоем, относительно декартовой системы координат (x, y) , а именно:

( K )

Жесткости слоя Q_IJ (I, J=1,2,6), коэффици-

енты температурного расширения a j

( K )

(J=1,2,6)

и деформации натяжения слоя

( K )

£ HJ

( J =1,2,6) в

m(K) = cos фK

n(K) = sin фK ,

- ( K )           - ( K )

^£ H — K hb ^£ B ,

(1), приведенные к осям панели, определяются через жесткостные и температурные характеристики слоя, заданные в системе координат (1, 2) с ним связанной, с учетом поворота последней относительно декартовой системы координат пластинки (x, y) . Соответствующие преобразо-

где K_НВ – безразмерный коэффициент, определяющий уровень натяжения и изменяющийся

(по модулю) от 0 до 1;     - допускаемая де-

£ В

( K )

вания для, Q _IJ

и

( K )

a j

представлены в работах

[2, 3, 4, 6]. Жесткости слоя, приведенные к осям панели, определяются соотношением:

2 ( K )

формация препрега “ k ”-ого слоя.

Модули упругости в направлении слоя E ₁ ^{( K} ) и перпендикулярно к нему E 2 ^K ) , соответственно, модуль сдвига G ₁ (2 K ) , коэффициенты Пуассона v ( K ) , v 2 K ) и коэффициенты температурного расширения a ₁ ^{( K} ) и a 2 ^K ) зависят от температурных свойств волокон и матрицы, а так же от сте-

где

-

Q ii

Q 12

„ ^Q 22

Q 66

Q 16

Q 26

m 4	2 m 2 n 2	n 4	4 m 2 n 2	( K )
m 2 n 2	4 . 4 m + n	m 2 n 2	- 4 m 2 n 2		' Q 11
n 4	2 m 2 n 2	4 m	4 m 2 n 2		Q 12
m 2 n 2	- 2 m 2 n 2	2 2 mn	( m 2 - n 2 ) 2		Q 22
3 m n	- mn ( m 2 - n 2 )	3 - mn	- 2 mn ( m 2 - n 2 )		. Q 66
3 mn	mn ( m 2 - n 2 )	3 - m n	2 mn ( m 2 - n 2 )

( K )

пени армирования слоя.

При записи физических соотношений в виде (1) не учитывается, что в препреге (слое) предварительно натягиваются лишь волокна, в то время как после снятия натяжения слой деформируется полностью.

Погонные нормальные и сдвигающие силы, изгибающие и крутящие моменты для всего пакета, действующие, например, по площадке, перпендикулярной оси x , определяются интегриро-

ванием соответствующих компонент напряженного состояния по толщине, что, с учетом гипотезы Кирхгофа дает:

H/2

N = J a (KK) dz; N = J т (K K) dz; x           x             xyxy

- H/2

H/2

Mx = J a(K) zdz;, Hiv = J т(K) zdz. x           x            xyxy

- H/2

следовательно, напряжения по формуле (1)

a x	( K )	" Q 11	Q 12	Q 16 "	( K )	^ 0	+ kx 'z - a ( K ) ! - - <, K ) x       1              H 1
a y \ry,	■ = 1	Q 12 _ S 16	Q 22 Q 26	Q 26 Q 66		- 0 z 0	+ K 0 z - a 2 K ) A T - - HK + K 0 y z - a ( K ) A T - - HK )	■ (12)

В системе координат, связанной с направлением армирования “ k ”-го слоя, напряженное состояние определяется посредством преобразования при повороте осей:

Отсюда и из (1) вытекают соотношения, связывающие внутренние силовые факторы с деформацией слоистого элемента:

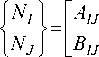
B ij "	J' £ J	J N T	J N H	\                ,
D ij _	1 k J	1 1 M T	1 1 M H	I , J = 1,2,6 (8)

,

⁽ x , y , xy )

a 1	( K )	m 2 n 2     2 mn	( K )	ax
a 2	■ =	n 2 m 2    - 2 mn 22		a y	■ .(13)
a 3		- mn mn ( m - n )		т xy

где N T , N T , N T _y , M T , M T , H T - “температурные” усилия и моменты.

В данной работе для слоя однонаправленного волокнистого композита используется тензорно-инвариантный критерий Гольденблата – Коп-нова, который записывается в виде:

{nt }= A T I Q„ ](K a}(K) F(K); k=1

{ M T } = A T I [ Q ij ] ^{( K} a } ^{( K} ) 5 ^{( K} ) I , J = 1,2,6 , ⁽⁹⁾ k ^{1                                      (} x , y , xy )

HHH H HH

a Nx , Nv , Nx..... Mx , Mv , Hxv - усилия и моменты x y xy    x     y xy от натяжения.

1 ( 1       1 )

?l   ^-~ Г ¹

²1 ^a 1     ^a 1 J

1 ( 1       1 )

+—Ila + о I —+    —- l 2

² ^ ( T ₂     (T 2 J

+

^a 1 ⁺

T ₁

T 1 ²

¹ I ^{1        1}   I           | ^T 12 I

⁺41 ■ ^-— l t 2 ⁺ I l

⁴ \ ^a 2    ^a 2 J      \ ^T 12 J

< 1 .(14)

N

{nH }=I Qj ](K—}(K1 F(K1;

k = 1

N

M } = I [ Q ij ] ^{( K} ) { ^ J } ^{( K} ) 5 ^{( K} )

k = 1

I , J = 1,2,6 .

⁽ x , y , xy )

В свою очередь, F ^{( K} ) , 5 ^{( K} ) , J ^{( K} ) - погонные площадь, статический момент и момент инерции “ k ”-го слоя соответственно.

Обобщенные жесткостные характеристики многослойной панели ( A IJ , B IJ , D IJ ) ( I, J =1,2,6) даны в работах [4, 6, 8].

Так как усилия и моменты согласно формулам (8) зависят как от деформации в плоскости панели, так и от кривизны поверхности приведения, в рассматриваемом случае из-за несиммет-рии свойств структуры пакета по толщине задача не разделяется на плоскую и изгиб пластинки.

Если известен столбец внутренних силовых факторов, в том числе температурных и связанных с натяжением, на основании равенства (8) путем обращения матриц могут быть найдены компоненты деформированного состояния

^ J . kJ

AIJ

BIJ

bij I-1 J NT + NH Dij J  [Ml + MH

Согласно критерию прочности Гольденблата-Копнова для однонаправленного слоя КМ, растрескивание или разрушение пакета не произойдёт, пока в каждом слое выполняется условие (14).

Следует отметить, что тензорная теория прочности является более общей, чем все другие теории, характеризуется инвариантностью относительно координатных осей, возможностью проведения преобразований в соответствии с обычными тензорными преобразованиями, симметрией прочностных свойств, подобной симметрии для жесткостей и податливостей и поэтому при проведении проектировочных расчетов может считаться более предпочтительной, чем другие [7].

Формоизменение или коробление изготавливаемых конструкций определяется рядом факторов, которые следует учитывать как при проектировании, так при изготовлении.

Формулы для прогиба W , а также для продольного U₀ и тангенциального V₀ смещений получены интегрированием соответствующих компонент вектора деформаций, когда кромки панелей свободны от закрепления:

W = -1(K°x .X2 + KXy .X.y + Ky .y2);

т т 0          'XV

U о = ^£ x •^{x +}—• y ;

Таблица 1. Схемы укладки слоев в пакете композита

Номер панели	Схем а укла дки паке та
1	0	15	-15	90
2	0	30	-30	90
3	0	45	-45	90
4	0	60	-60	90
5	0	75	-75	90

Рис. 1. Распределение приведенных эквивалентных остаточных температурных напряжений в зависимости от углов укладки ± θ , V_B = 46%, К _НВ = 0:

1 - (00/±150/900); 2 - (00/±300/900); 3 - (00/±450/900); 4 - (00/±600/900); 5 - (00/±750/900).

V 0 = 8 0- y + Y y- ■ X .          (15)

Учитывая важность данной проблемы, с помощью программы, разработанной в соответствии с изложенным выше алгоритмом на языке ФОРТРАН, было исследовано влияние предварительного натяжения волокон, процентного содержания компонентов композита на прочность несущих слоев многослойных панелей при автоклавном методе изготовления (температура отверждения Т=175⁰ С , разница между начальной температурой и температурой отверждения ДТ= - 155⁰ С ). Несущие слои имеют вид четырехслойных углепластиковых пластин со схемами укладки пакета (0⁰/± θ ⁰/90⁰). Уровень предварительного натяжения волокна изменялся ступенчато от 0 до 40% от допускаемой деформации волокна ε _в с приращением 0.2 ⋅ ε _в . Параметрический анализ выполнен при варьировании взаимной ориентации слоев в пакете (0⁰/ ± θ ⁰/90⁰) и степени армирования слоя ( V_B = 46%, V_B = 60%, V_B = 76%).

Материал слоев – углепластик КМУ - 4Л.

Толщина элементарного слоя равна 0,11 мм, зависимость эквивалентных остаточных напряжений от степени армирования слоя для различных схем укладок (0⁰/±и⁰/90⁰) без учета предварительного натяжения показаны на рис.1-2. За исключением укладок (0⁰/±15⁰/90⁰) и (0⁰/±75⁰/ 90⁰), заметен рост уровня максимальных остаточных напряжений с увеличением V_B . При достижении V_B = 76% происходит растрескивание для всех схем укладок пакета композита, изготовление их в таком режиме становится невозможным. Для укладок (0⁰/±15⁰/90⁰) и (0⁰/±75⁰/ 90⁰) происходит незначительное падение уровня максимальных эквивалентных остаточных напряжений с V_B = 46% до V_B = 60% и затем повышение их значения. При V_B = 76% величина у_экв превосходит 1. Как видно из приведенных результатов, эквивалентные остаточные напряжения могут достигать значений, сопоставимых со значениями прочности материала.

Роль и влияние предварительного натяжения волокон на прочность панелей из углепластика при изготовлении можно оценить, сравнивая значения максимальных остаточных эквивалентных напряжений, показанных на рис. 3-5.

1----(O’/iirW) 2----(О’УО’ЭД") 3----(0e;±4S*/90’)

4----(0°;±60^eW) 5---- №'4=15°>W)

Рис. 2. Распределение приведенных эквивалентных остаточных температурных напряжений в зависимости от углов укладки ± θ , V_B = 60%, К _НВ = 0:

1 - (00/±150/900); 2 - (00/±300/900); 3 - (00/±450/900); 4 - (00/±600/900); 5 - (00/±750/900)

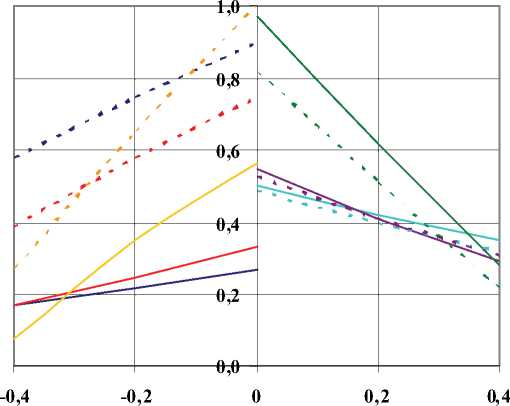
1 234 56

1-1          2-2          3-3          4-4           5-5          6-6

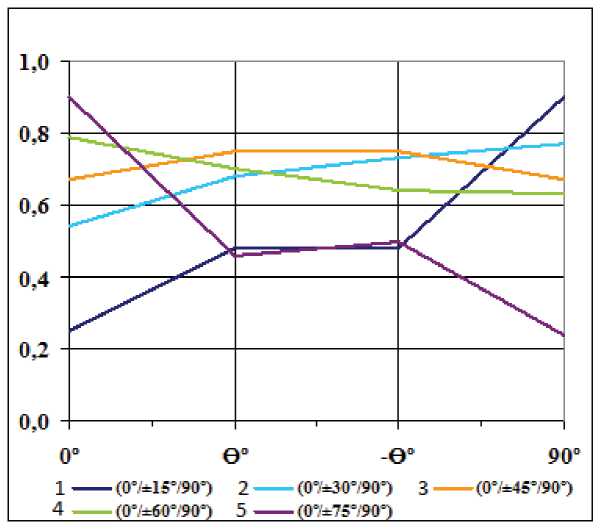
Рис. 3. Влияние уровня натяжения волокна при различной степени армирования слоя на распределение приведенных остаточных температурных напряжений с углами армирования (0⁰/±15⁰/90⁰):

• 1    - V_B = 46%, θ = 0⁰; 1-1 - V_B = 46%, θ = 90⁰; 4 - V_B = 46%, θ = 15⁰; 4-4 - V_B = 46%, θ = -15⁰;

• 2    - V_B = 60%, θ = 0⁰; 2-2 - V_B = 60%, θ = 90⁰; 5 - V_B = 60%, θ = 15⁰; 5-5 - V_B = 60%, θ = -15⁰;

• 3    - V_B = 76%, θ = 0⁰; 3-3 - V_B = 76%, θ = 90⁰; 6 - V_B = 76%, θ = 15⁰; 6-6 - V_B = 76%, θ = -15⁰.

  Характер приведенных кривых (рис. 3-5) ^ экв = f (К нв ) идентичен. При всех углах ори ентации слоев и степени армирования слоя V_B = 46%, V_B = 60%, V_B = 76%, с увеличением уровня предварительного натяжения волокон приведен-

  
  

  ные напряжения падают. Чем выше степень армирования слоя, тем эффективнее влияет предварительное натяжение волокон на прочность панелей после отверждения - увеличивается градиент построенных кривых:

  
  
  

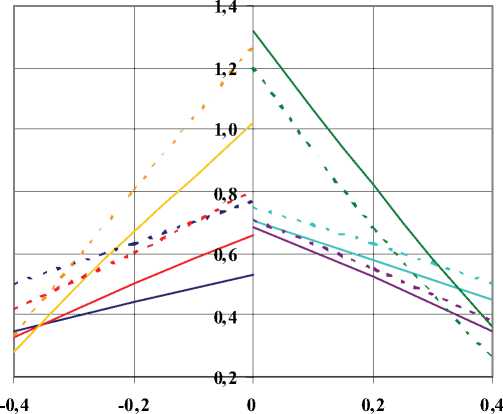
  123 456

  1-1            2-2           3-3            4-4            5-5            6-6

  
  

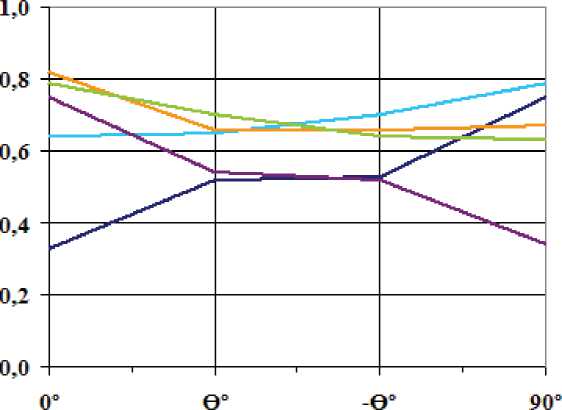
  Рис. 4. Влияние уровня натяжения волокна при различной степени армирования слоя на распределение приведенных остаточных температурных напряжений с углами армирования (0⁰/±30⁰/90⁰):

  1 - V B = 46%, 0 = 0 0 ; 1-1 - V B = 46%, 0 = 90⁰; 4 - V B = 46%, 0 = 30⁰; 4-4 - V B = 46%, 0 = -30⁰;

  2 - V B = 60%, 0 = 0⁰; 2-2 - V B = 60%, 0 = 90 0 ; 5 - V B = 60%, 0 = 30 0 ; 5-5 - V B = 60%, 0 = -30⁰;

  3 - V B = 76%, 0 = 0⁰; 3-3 - V B = 76%, 0 = 90 0 ; 6 - V B = 76%, 0 = 30 0 ; 6-6 - V B = 76%, 0 = -30⁰.

  
  
  

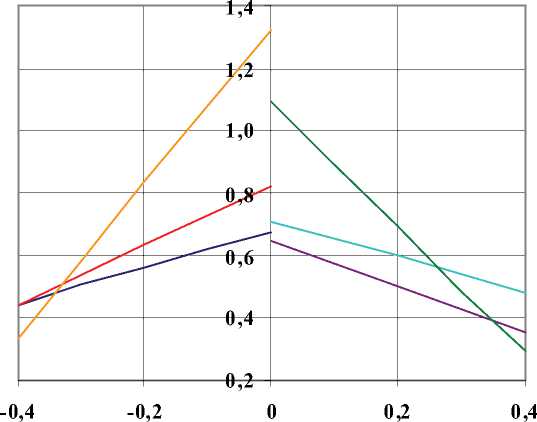
Рис. 5. Влияние уровня натяжения волокна при различной степени армирования слоя на распределение приведенных остаточных температурных напряжений с углами армирования (0⁰/±45⁰/90⁰):

1 - V B = 46%, 0 = 0⁰; 4 - V B = 46%, 0 = 45 0 ; 2 - V B = 60%, 0 = 0⁰; 5 - V B = 60%, 0 = 45 0 ;

3 - V B = 76%, 0 = 0⁰; 6 - V B = 76%, 0 = 45 0 .

5^3K6

(5| К нв\

>

5^3K6

7 V = 76% V в

S| ^™l

>

5^3K6

7 V = 60% V в

S| ^™l

7 V = 46% в

Изготовление панелей с V_B = 76% становится возможным (рис. 3-5), если армирующие волокна предварительно натянуты до 0.09 • е в для панелей типа 2 - 4, и до 0 03 • е - для па в

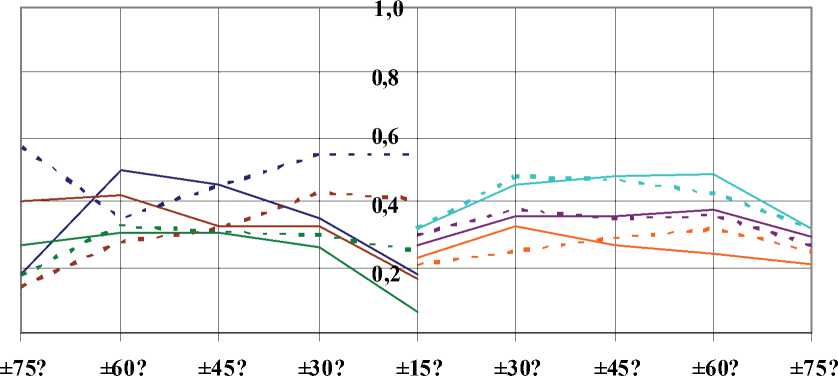
■ ■ ■ I 1-1 ■ ■ ■ 2-2 .... 3-3 ■ ■ ■ 4-4 ■ ■ ■ I 5-5 .... 6-6

Рис. 6. Влияние углов армирования (0⁰/±и⁰/90⁰) и степени армирования слоя при уровне натяжения волокна К _НВ = 0.4, на распределение приведенных остаточных температурных напряжений (критерий Гольденблата - Копнова):

1 - V_B = 46%, θ = 0⁰; 1-1 - V_B = 46%, θ = 90⁰; 4 - V_B = 46%, θ = (15...75)⁰;

4-4 - V_B = 46%, θ = -(15...75)⁰; 2 - V_B = 60%, θ = 0⁰; 2-2 - V_B = 60%, θ = 90⁰;

5 - V_B = 60%, θ = (15...75)⁰; 5-5 - V_B = 60%, θ = -(15...75)⁰; 3 - V_B = 76%, θи = 0⁰;

3-3 - V_B = 76%, θ = 90⁰; 6 - V_B = 76%, θ = (15...75)⁰; 6-6 - V_B = 76%, θ = -(15...75)⁰.

нелей типа 1, 5.

Влияние углов армирования и степени армирования слоев в пакете при предварительном натяжении волокон 0.4 ⋅ ε _в показаны на рис. 6. Уровень максимальных эквивалентных остаточных напряжений принимает наименьшее значе ние при V_B = 76%.

При углах ориентации θ = ±45⁰ значения σ _экв для 1-го и 4-го, а также 2-го и 3-го слоев совпадают. В слоях 0⁰ и 90⁰ - σ _{эк в} принимают максимальное значение и равны σ _экв = 0.335 .

Таким образом, с точки зрения практики проектирования панелей из углепластика рациональным вариантом можно считать панели, изготовленные с учетом предварительного натяжения волокна, так как уровень максимальных напряжений, имеющих место при отверждении в этом случае ниже, а разброс распределения их по слоям незначителен.