Анализ тепловых и рекомбинационных потерь фототока в солнечных элементах космических аппаратов

Обсудим эту проблему, считая, что именно за счет повышения параметров лицевого слоя можно увеличить КПД СЭ в целом на несколько процентов.

Уравнения баланса. Для расчета вольт-амперной характеристики (ВАХ) СЭ используем следующие уравнения переноса носителей тока:

д j„            A n

4= = gn (x)--, ax           T „ djp      ( x Ap

— = g p ( x) , a x            ^t p

где j n и j p – потоки электронов и дырок; Δ n и Δ p , g n и g p , τ n и τ p – их неравновесные концентрации, скорости генерации и времена жизни носителей тока, соответственно.

Эти же уравнения могут быть представлены также и в интегральной форме:

J_n = G_n – R_n – J_ns ,

Jp = Gp – Rp – Jps, где Jn и Jp – потоки электронов и дырок через p–n+-пе-реход; Jns и Jps – их рекомбинационные потоки на внешней поверхности СЭ (электронов – на тыльный контакт, дырок – на лицевую поверхность); Gn и Gp, Rn и Rp – скорости генерации и рекомбинации электронов в p-базе, дырок – в лицевом n+-слое.

Аналогичные уравнения могут быть записаны и для баланса энергии фотона в структурах СЭ.

Представим его в виде

W = Qa + Qt + Qr + Qp + Qp + J (V+Vk).(4)

Здесь приняты следующие обозначения.

Общий поток энергии излучения в СЭ:

W = E hVGv .(5)

h v> 0

Поток энергии нефотоактивной части излучения:

Qa = E hv Gv .(6)

h ^V g

Эта часть излучения поглощается в структурах СЭ за счет излучения фотонов, также на тыльных электродах и примесных атомах (ε g – ширина запрещенной зоны).

Кинетическая энергия фоточастиц, термолизация которых приводит к нагреву материала СЭ ( Q T – энергия термолизации):

Qt =E (hv-eg)Gv .(7)

h v>e g

Энергия, выделяемая при рекомбинации неравновесных носителей заряда (ННЗ):

Qr = R ■£g .(8)

Энергия, выделяемая в p – n -переходе:

Qnp = JqVnp,(9)

где V np – высота p – n -перехода в рабочем режиме (рис. 1, 2).

Омические потери в n ⁺-канале:

Ф 0

Q p = J J ( ф ) d _Ф ,               (10)

v где J(ф) - фототок, dф = ф0 - v - падение напряжение в канале освещаемой площадки СЭ до собирающего электрода.

Кроме того, в (4) V – выходное напряжение;

V k – контактная разность потенциалов полупровод-ник–электроды.

Замечая, что согласно (3),

R = G – J , R = R n + R p ,

J = J n + J p + J ps ,    G = G n + G p ,        (11)

из уравнений (4)–(8) находим

J e g = Q np + Q p + J(V + V k ) q .          (12)

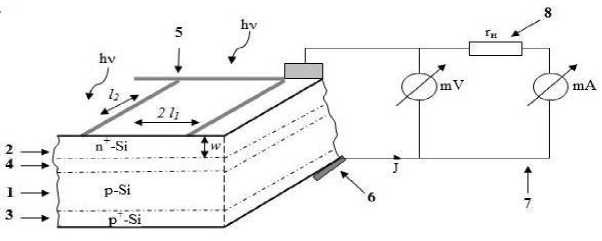
Рис. 1. Фрагмент структуры СЭ, схема измерений ВАХ:

1 – базовая p -область СЭ; 2 – высоколегированный тонкий слой n ⁺-Si; 3 – высоколегированный слой p ⁺-Si; 4 – p – n ⁺-переход; 5 – собирающий электрод; 6 – металлизация тыльного электрода; 7 – электрическая цепь измерения;

8 – нагрузочное сопротивление r н

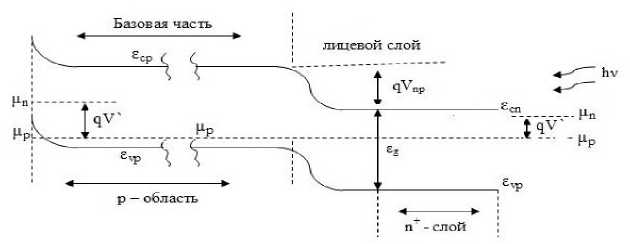
Рис. 2. Зонная структура СЭ в рабочем режиме:

μ n и μ p – уровни Ферми в n ⁺- и p -областях; qv = μ n – μ p ; ε cn – ε vn = ε cp – ε vp = ε g , ε cn – μ n + μ p – ε vp = qV k ; ε cp – ε cn = qV np ; V ′ – падение напряжения во внешней цепи с учетом омических потерь в n ⁺-слое

В режиме холостого хода, когда J = 0 и V = Vхх, имеем Qp = 0 и Qnp = JVnpq и, следовательно, s g = q (Vp + Vk),               (13)

где qV_n ⁰ _p – высота p – n ⁺-перехода СЭ в термодинамическом равновесии, определяемая уравнением [1]

qV p = kT ln NN- ,           (14)

ni где q – элементарный заряд; Na, Nd, ni – концентрации соответственных акцепторов в базовой области и доноров в ЛС.

Независимо от того, является ли контакт омическим или нелинейным, при прохождении тока на нем выделяется тепловая энергия, известная как теплота Пельтье:

Q n =n J .                 (15)

Здесь коэффициент Пельтье (П) может быть оценен по формуле [2] для n -полупроводника:

n _n = kT fc + 5 + In — |              (16)

q v 2 n )

и подобной формулой для p-полупроводника с заменой «n» на «p» и zn на zp, где zn, zp – плотности состоя- ний электронов и дырок, σ – показатель степени свободного пробега – энергия в тепловых столкновениях носителей тока, σ = – 2 для кремния.

Формула (16) справедлива для невырожденного полупроводника. В нашем случае – для базовой области, в которой концентрация дырок p ≈ 1016 см–3 и kT (

Пp = — I 2 + In -p I,(17)

q V где zp ≈ 1019 см–3 – плотность состояния дырок в кремнии. Получаем Пp ≈ 0,23 В.

Что касается ЛС, то здесь концентрация электронов достигает 10²⁰…10²¹ см^–3 и, следовательно, полупроводник вырожден. Коэффициент Пельтье вырожденного полупроводника отрицателен и мал (П <  kT / q ≈ 0,026 В). Тепло выделяется на контактах базы: на тыльном и на границе с p – n ⁺-переходом. Это проявляется в потере напряжения в цепи СЭ порядка П ≈ 0,23 В, что существенно.

Влияние рассредоточенности омических потерь в ЛС на ВАХ СЭ и потери мощности фототока в их структурах. Фототок J(φ) в лицевом слое (ЛС) СЭ возрастает, а напряжение φ падает от середины ЛС. Когда J = 0, а φ = φ0, по направлению к электродам, где ф = V, это описывается дифференциальными уравнениями [3-5]

dJ (Ф) = l j дx      2 Jnp’

дф д x

--p J ( Ф ), I2 W

где 0 <  x <  I 1 , I 1 - протяженность собирающего канала ( n ⁺-канала ЛС); р - его удельное сопротивление; w - эффективная толщина; 1 ₂ - протяженность собирающего электрода.

Плотность фототока через p - n -переход здесь обозначена j_np и определяется формулой

С учетом того, что собирающие электроды СЭ имеют П-образный вид, выражения (24) и (25) обобщаются: А Vр ~ eJ-, где в - эмпирический параметр (0,33 < в < 0,5). В этом приближении ф0 = V + АVр и уравнение (20) приводится к виду qv

J = 2 ₽ ( J _v+ J 0 ) - J 0 e^kTF ( а ),          (26)

k- ш . eа-1 где а =---, F (а) ®----- qVp         а

В [3; 4; 6] уравнение (26) отличается от нашего тем, что в нем 2в = 1 и F (а) ~ e ^а.

Тепловые потери фототока непосредственно в p-n+-переходе определяются по формуле q Ф jnp = jv- jо(ek -1).               (19)

Ниже

₁ ]                                  V +A V _p Т / X

Q np =j ( V p -Ф ^ ( ф ) 1 2 dx = J —. (27)

О '                V    J ( ф ) -

J np = ^jnp l 1 ¹ 2 , ^J v = ^j v ¹ 1 ¹ 2 , ^J 0 = ^j 0 ¹ 1 ¹ 2 ,

где 1 1 , 1 ₂ - освещаемая площадь СЭ; j_v и j ₀ - плотности фото- и обратного темнового токов через p - n ⁺-пе-реход.

Как показано в [5], интегрирование уравнений (18)

В приближении А V _р <<  V оценки Q_np можно производить по более простой формуле

Q » ¹ J (V⁰ - V ).              (28)

~ np   2 np^ np

приводит к следующему выражению для в ЛС:

фототока

rJ ²

— = Ф ( Ф 0 ) -Ф ( V );

Что касается рекомбинационных потерь Q R _n в базовой области и Q Rp - в ЛС, то их можно определить по формуле (8):

Q_R n = s g R n = s g ( G n - J n ), Q_R p = s g ( G p - J p ) (29)

р 1 где - = —- w1 ₂

—

омическое сопротивление

участка,

или из уравнений

¹ n ⁺ xn

0 <  x <  1 1 - лицевого слоя, а

1            1

’Rn =— A N = — j A n ( x ) dx , ^T n         ^T n -

irp       q ^ф

Ф ( ф ) = ( J v + J 0 ) ф- — J 0 ( e^kT - 1). ^q

xn xn

Омические потери в n ⁺- канале следует вычислять по формуле

1               1 г , , ,

'Rp = — A P = — f A p ^{( x} ) ^dx .

^T p       ^T p 0

Ф 0

Q p = J ^{J (} ф ) d ф ,

V

Здесь А n ( x ) и А p ( x ) должны быть решениями уравнений (1) и (2) при соответствующих граничных условиях:

в которой так же, как и в (21), потенциал ф0 должен быть определен независимым путем. В частности, из второго уравнения (18) находим ф - V = AVp= J J(x)pdx, (23) 0 12 w где 11, 12 - геометрические параметры n+-канала: р - удельное сопротивление, J(x) - фототок в канале на расстоянии х от середины освещаемой площадки СЭ по направлению к электроду.

В приближении малых омических потерь следует:

J n ( x n + 1 n ) = 0, J n ( x n ) = J nv , J p ( x n ) = J pv , J p (0) = J ps ,

записанных с учетом того, что поток электронов через тыльный контакт практически отсутствует (контакт с изотипным p - p ⁺-переходом), а в ЛС - поток J_ps определяется поверхностной рекомбинацией. В приближении J_ns = 0 и 1_n >  L_n решение уравнения (18) известно [7]:

jnv

q^g ° ^{а v}Lⁿ e ~^а Ln (1 + f ) ( а _vL n + 1)      ^V

f =

^а v L n e ^v n

_    J ²г           1

Q p” — и A V p = - J(V ) - .       (24)

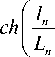
Значения для А V _р , полученные в [3]:

A V p = 3 J ■ - , J = J ( V ).             (25)

При a v 1 n >> 1, f << 1

_ ¹ n

G n = qg 0 e "^а vxn (1 - e^Ln ).              (34)

Эти выражения совместно с уравнением (29), в ко-qV тором Jn = Jnv + J0n + J0nekT F(а), решают проблему оценок QRn. Что касается потерь QRp = Gp – Jp, то для их оценок необходимо учесть особенности ЛС: наличие в нем тянущего поля и рекомбинации дырок на внешней поверхности ЛС. Ниже мы анализируем Jp, Rs с учетом этих факторов.

Эффект сильного поля в лицевом слое СЭ: влияние его на R-потери и эффективность фотопреобразования ЛС. Тянущее поле в ЛС создается как градиентом доноров:

кт a

E =----ln N d ( x ),            (35)

q dx так и внешним источником – контактными зарядами на ПС и в диэлектрике (Ee).

Поток дырок j_p имеет две составляющие:

j_P = qp ц p^{E -} q— ⁽ D p P ).         ⁽³⁶⁾

d x

Первый член – это дрейфовый поток, второй – диффузионный.

Условием сильного поля в ЛС может служить неравенство

Δ t E << Δ t D ,                  (37)

где Δ t_E – дрейфовое время пролета дырок ЛС;

l p                                          q

A t_E =---, где l_p - толщина ЛС; ц = —D - под-

E цpE                         p kT p lp2

вижность дырок в ЛС; A t_n = —— ^D 2 Dp

–

диффузионное

время пролета расстояния l p . Из (37) следует

Интегрирование этого уравнения дает

x

A p = - g 0 ^{T p} e ^a v ^x + Be ^{Х p} .          (42)

aX- 1

Из граничного условия

d(A p ) _n , = 0 при х = L

8x находим:

lp

B = g0T e"vlpeХp(43)

a v Х- 1

и st           -(av-/ )lp

Ap (0) = -4^- (1 - e    "p ).(44)

^a v ^{Х- 1}

Поток дырок в p – n -переходе можем определить с помощью уравнения (2) в интегральной форме:

jp (Ip) - jpS (0) + — AФ p = g0 (1 - evlp).(45)

t p

Здесь gaTpXp e^a*ip (1-e)- i-e-^ a v Х-1      V 7    a v Х lp

AO = j A p ( x ) dx ^

. (46)

В результате из (45), (44) и (46) находим jp (lp) = jps (0) +       (1 - eV 4, a v Х-1\ a =a v -— .               (47)

x„

Уравнение (44) приводит к следующему выражению для j ps (0):

2 D

E >>--- .

Ц p l p

jps

g ^t ( aX- 1)

N_s a° p

*

1 - e ^{-a plp}

Замечая, что D p /μ p ≈ 2,5∙10^–2 эВ и учитывая, что l p в СЭ n⁺–p-Si типов l p ≤ 5∙10^–5 см, получаем E >> 10³ В/см. Непосредственно в p–n⁺-переходе E ≥ 10⁵ В/см, а в узком лицевом слое поле на порядок меньше, но условие (38) выполняется. Это означает, что в ЛС перенос дырок осуществляется под действием тянущего поля и поэтому

Из (47) и (48) находим следующее отношение потоков дырок из ЛС на ПС и в n ⁺– p -переход:

p ( l p ) 1 + v в j ps (0)       a ⁰ p N s

Условиями малости рекомбинационных потерь является χ >> 1 или jP = qp Ц pE .               (39)

v p =ц p E >>a° p N_s в - ¹ .            (50)

При этом уравнение (2) с учетом того, что gp (x) = g0eavx,             (40)

где α v – коэффициент поглощения света, переписывается в виде

S(Ap) Ap        vx vp dx     . p   g0 e

⁽ v p =Ц p E , ^Х p =Ц p E ^t p )•

Обычно N_s ~ 10 '2 ^10 '3 см^-2, a p ~ 10 9 ^10 8 см³/с и P - ¹ << 1, поэтому ц _pE >> 10 3 ^10 5 см/с, что практически реализуется в ЛС современных СЭ.

Минимизация рекомбинационных потерь фототока в ЛС СЭ. Поверхность раздела сред полупроводник–диэлектрик всегда содержит определенное количество поверхностных состояний (ПС), залегающих в запрещенной зоне полупроводника, на которых осуществляется рекомбинация неосновных носителей тока (ННТ). Поверхностная плотность этих состояний Ns и их параметры зависят от физических свойств граничащих сред и дефектного состава поверхности. Рекомбинационный поток ННТ на ПС согласно модели Шокли [1] определяется формулой js   jps

« n « p N s ( ⁿ P - ^)

« n ⁽ M s + ⁿ i ) ^{+ a} p ⁽ P s ⁺ P 1 ) .

Здесь n s и p s – концентрации электронов и дырок у границы раздела сред; α n и α p – коэффициенты (скорости) захвата ННТ на ПС; n 1 и p 1 – параметры ПС:

ⁿ i = z n Y ns , P 1 = z p Y ps , ⁿi P 1 = n²

^£ -£ ^           Г £ -£ ^

Y_ns = exp —---- , Y = exp —^s ---^u ; (52)

ns          kT ps            kT zn и zp – плотности состояний электронов в свободной зоне и дырок – в валентной; ni – концентрация носителей тока в собственном полупроводнике; A£s = £c - £s - глубина залегания ПС в запрещенной зоне.

Общепринятой считается модель теплового равновесия носителей тока в объеме и поверхности полупроводника, согласно которой [1]:

n s = n в s , P s = P в - 1 ,                (53)

о     (qфЛ

где в _s = exp I---I , ф _s — поверхностный потенциал;

V kT J n и p – концентрации электронов и дырок в объеме полупроводника.

Для описания рекомбинации ННТ в ЛС на границе с диэлектриком более справедливой является модель динамического равновесия между электронами в объеме полупроводника и на ПС. Согласно этой модели концентрация электронов на ПС

Nf = Ns (ann +apP1 )

s ^{s a} n ^{( n}s ^{+ n}i ) + a P ⁽ P s + P 1 )

В сильном электрическом поле в ЛС концентрация дырок и скорость их захвата на ПС а 0 в - 1 A p малы и тогда рекомбинационный поток j ns = j ps также будет мал. Как отмечено выше, для создания сильного поля необходимо обеспечить технологию высокого градиента легирующей примеси в ЛС. Обычно градиентное поле E в лицевом слое n ⁺– p -Si СЭ достигает ~10³ Вт/см и более. В принципе эффект поля можно усилить за счет контактной разности потенциалов на поверхности полупроводник–поверхностный диэлектрик. Как правило, любой диэлектрик обладает радиоэлектронным эффектом. Под действием ультрафиолетового солнечного излучения в электроде создается электрическое поле с контактным потенциалом Δφ k не менее половины ширины запрещенной зоны диэлектрика; оно может достигать 3…4 эВ при ширине запрещенной зоны диэлектрика 7…9 эВ. При этом на границе полупроводника, где расположен ПС, напряженность электрического поля возрастает до 10⁴…10⁵ В/см. Этого достаточно, чтобы ограничить доступ дырок к ПС.

Более точная оценка контактных полей, зарядов и потенциалов на поверхности ЛС затруднена из-за отсутствия информации об электрофизических свойствах и распределения дефектов у границ раздела сред. Из физических соображений следует, что в ЛС действительно много дефектов. Их образование обусловлено прежде всего тем, что n ⁺-слой представляет собой материал, перенасыщенный фосфором до пределов растворимости ( N d ~ 10²⁰…10²¹ см^–3). Это приводит к распаду раствора с выделением второй фазы с участием атомов кислорода ( N O ≈ 10¹⁸ см^–3) и частично углерода ( N С ≈ 10¹⁷ см^–3) и бора ( N B ≈ 10¹⁶ см^–3). Следует предполагать, что в таком ЛС кроме точечных дефектов (A-центров, Е-центров, акцепторнодонорных пар и других комплексов) образуются также и структурные дефекты. Они обнаруживаются по избыточному току обратно смещенного n ⁺– p -пере-хода СЭ, который на порядок выше теплового тока:

определяет заряд ПС и, следовательно, его потенциал φ _s , а скорости захвата α _n и α _p регулируются высотой потенциального барьера q φ s в соответствии с уравнениями

^J изб >>  J о = q

п D р D ^ pn  pn p

.

L L I

V n p J

a = a0B ,a = a0B 1, nns, p ps,

при этом n s ≡ n и p s ≡ p .

Уравнения (51) и (54) для этого случая приобре-

тают вид

. = . =       N s ^a 0 ^a P ( ⁿP ~ ⁿ 2 )

^jns ^{jpS a} 0 ^в s ( ⁿ + ⁿ i ) + ^a P ^в - 1 ( P + P 1 ) ,

f =       a0n в s +в-1aPP1

s anвs (n + n1 ) + aPв-1 (P + P1).

В приближении n >>  p и Δ p >>  p ≥ p ₁ , справедливым для ЛС, из (56) имеем

. ~ N s ^A P ^ns ~  2в s

.

Те из структурных дефектов, которые оказываются в области объемного заряда n ⁺– p -перехода, выявляются также с помощью микроплазм, возникающих при повышенном ( V обр > 5 B) обратном напряжении [8].

Все эти дефекты ухудшают электрофизические свойства ЛС: увеличивают омическое сопротивление и уменьшают время жизни ННТ (дырок). Необходима технология ( n ⁺-слоя), которая бы обеспечивала максимальную электропроводность ЛС с максимальным градиентным (тянущим) полем и максимальной контрольной разностью потенциалов (КРП).

В заключение следует отметить, что количественная оценка фотоэлектрической эффективности ЛС может быть произведена по вышеприведенным уравнениям и формулам после уточнения концентрационного и дефектного состава ЛС и ПС, а также изучения

влияния излучения на КРП границы ЛС с диэлектриком. Прежде всего необходимы электронно-микроскопические исследования состава и распределения примесей и дефектов в поперечном сечении ЛС. Очень важной могла быть информация о зависимости электропроводности n ⁺-канала от электрического режима СЭ (в частном от выходного потенциала V ).