Анализ термоупругих напряжений в поковках с учетом эффекта релаксации

Появление флокенов, т. е. заполненных водородом трещин, при охлаждении поковок обусловлено выделением водорода в микротрещины вследствие уменьшения растворимости водорода в α-железе и их роста из-за непрерывного возрастания давления газа молизующегося водорода H 2 [1]. Заметное влияние на рост флокенов оказывают термические напряжения [2]. Температурный интервал образования флокенов составляет 200…20 °С. Поэтому анализ напряжений необходим, прежде всего, для низкотемпературной области на заключительной стадии охлаждения поковок.

В работе [3] был выполнен аналитический расчет напряжений в охлаждаемых поковках, основанный на известных уравнениях термоупругости [4]. Прежде всего, он подтвердил, что «амплитудные» величины напряжений σ z , σ r и σ θ зависят от разности температур между поверхностью и осью цилиндра.

Максимальные значения растягивающих напряжений σ _z , и σ_θ наблюдаются у поверхности, тогда как сжимающих – в центре. Таким образом, при движении вдоль радиуса они изменяют свой знак. Напряжение σ _r только сжимающее. У поверхности оно равно нулю, а максимум модуля наблюдается у оси.

По мере возрастания длительности охлаждения разность температур между центром и поверхностью цилиндра уменьшается, соответст- венно, снижаются величины всех напряжений, а при достижении осевой зоной комнатной температуры упругие напряжения должны исчезнуть. Именно в этом заключается основной недостаток предыдущих расчетов, поскольку имеются данные [5] о сохранении в поковках остаточных напряжений. Этот эффект связан с явлением релаксации на различном расстоянии от оси. В данной статье обсуждаются результаты расчёта термических напряжений с учетом их релаксации в охлаждаемых поковках их стали 40ХГМ, поставляемой ОАО «Уральская кузница» на экспорт, а потому технологические аспекты её тщательно изучаются.

Методика расчета и обсуждение результатов

В основе использованного метода анализа лежат следующие соображения [6, 7]. Допустим, что образец с исходной длиной l0 был упруго растянут так, что его удлинение составило Δl0, а затем зане-волен. Упругие напряжения в таком образце будут A равны а0 = E---= Eб0, однако в ходе выдержки l0

длительностью τ при повышенной температуре воздействие напряжения приводит к ползучести, создающей пластическую деформацию εп, что уменьшит упругую деформацию и напряжение,

а            1 да(т, T)

так как теперь б₀ = — + б или------- = -б .

0 E ^п E дт

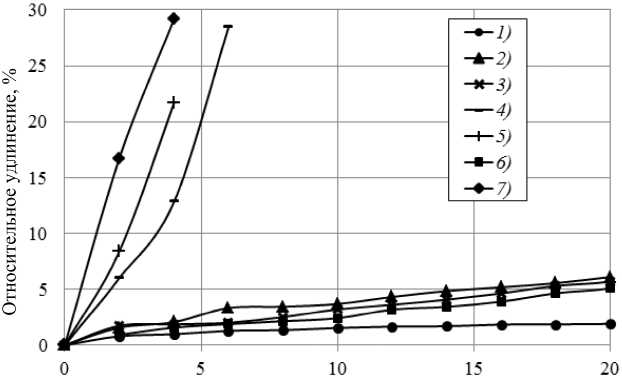
Время, ч

Рис. 1. Кривые ползучести стали марки 40ХГМ при различных параметрах испытания (температура-нагрузка): 1 – 560 °С, 150 МПа; 2 – 560 °С, 220 МПа; 3 – 600 °С, 150 МПа; 4 – 600 °С, 190 МПа; 5 – 600 °С, 230 МПа; 6 – 650 °С, 90 МПа;

7 – 650 °С, 150 МПа

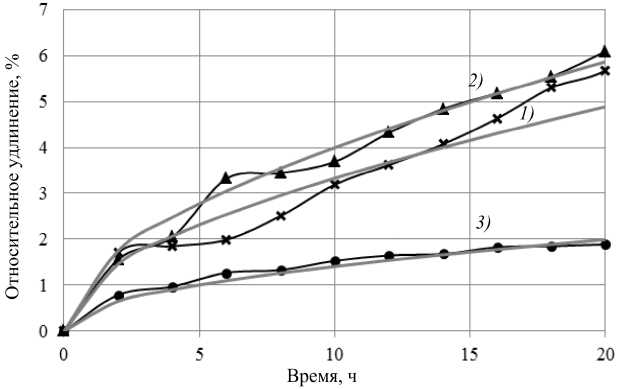
Рис. 2. Сравнение значений аппроксимирующей функции с экспериментальными данными для ползучести стали марки 40ХГМ: 1 – 560 °С, 150 МПа;

2 – 560 °С, 220 МПа; 3 – 600 °С, 150 МПа

Следовательно,

-1 d о ( т , T ) = ^- d s _n,                         (1)

E то есть развитие ползучести приводит к уменьшению (релаксации) напряжения. Если для данной стали известна деформация ползучести εп как функция напряжения и температуры, то уравнение (1) позволяет установить связь дифференциалов напряжения и деформации ползучести, необходимую для численных расчетов. В справочных данных пакета конечно-элементного моделирования ANSYS для деформации ползучести приведены несколько аппроксимирующих функций εп(τ, T), на основе которых построены программы численного интегрирования уравнения (1) для всех компонент тензора напряжений совместно с уравнениями теплопроводности и термоупругости.

С целью подбора функции εп(τ, T) было про- ведено экспериментальное исследование на ползучесть образцов стали 40ХГМ. От промышленной поковки стали 40ХГМ в кузнечно-прессовом цехе ОАО «Уральская кузница» были вырезаны заготовки 30x30x200 мм из середины радиуса поковки. Затем заготовки были подвергнуты отжигу по режиму: нагрев до 850 °С, выдержка 3 ч, охлаждение 2 ч с печью, далее на воздухе. Данный режим позволил получить в заготовках равновесную ферритоперлитную структуру, такую же, как после проти-вофлокенного отжига. Далее из заготовок были выточены стандартные образцы на ползучесть с диаметром рабочей части 7 мм и произведены испытания по ГОСТ 3248–811. Испытания на ползу- честь производились по нескольким вариантам при температурах 560–650 °С, соответствующих температурному интервалу охлаждения поковок после отжига, т. е. получены кривые ползучести (рис. 1, 2).

В качестве аппроксимирующей функции была выбрана функция общего вида

° C C3 +1 - CT   1, e =  + C ° 2 т 3 e 4

• п E 1

+C5°C6e-C7Tт , (2) для которой неизвестные коэффициенты С1, С2, …, С7 были определены путем последовательного сопоставления с экспериментальными зависимостями (еп )T=const = f1 (°) ; (еп Unst = f 2 (T) и т. д. Для областей нестационарной и стационарной ползучести: С1 = 78; С2 = 2,17; С3 = –0,55; С4 = 14 000; С5 = 750,4; С6 = 4,55; С7 = 28 240. На рис. 2 (1–3) сравниваются экспериментальные кривые зависимости и их аналитическая аппроксимация; степень их согласия можно признать достаточно хорошей.

Расчет напряжений о z , с r , о д и ст при охлаждении цилиндрических поковок с учетом релаксации был проведен в пакете ANSYS путем совместного численного решения методом конечных элементов уравнения теплопроводности, возникновения упругих напряжений и уравнения вида (1) для релаксации.

Параметры расчета были приняты такими же, как в работе [3]. Рассматривается цилиндрическая поковка из стали 40ХГМ диаметром 450 мм.

Для того чтобы установить влияние релаксации напряжений на распределение их по сечению поковки, будем сравнивать соответствующие зависимости напряжений σ _z , σ _r и σ_θ от r , рассчитанные с учетом и без учета эффекта релаксации. В программном комплексе ANSYS удалось рассчитать внутренние напряжения для различных скоростей охлаждения:

• 1)    на воздухе (рис. 3 и 4), при этом коэффициент теплоотдачи α, как и в работе [3], был принят равным 34 Вт м ² К ;

  С учётом релаксации

  
  
  
  
  
  

  в )

  
  
  
  

  ж)

  
  

  Без учета релаксации

  

  ------его

  
  
  

  з)

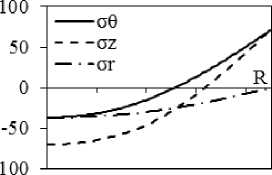
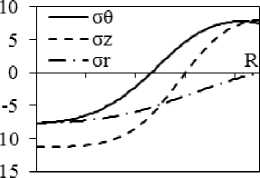
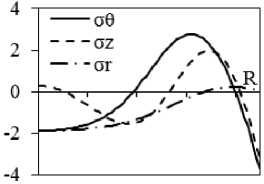
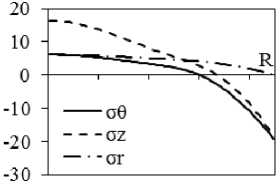
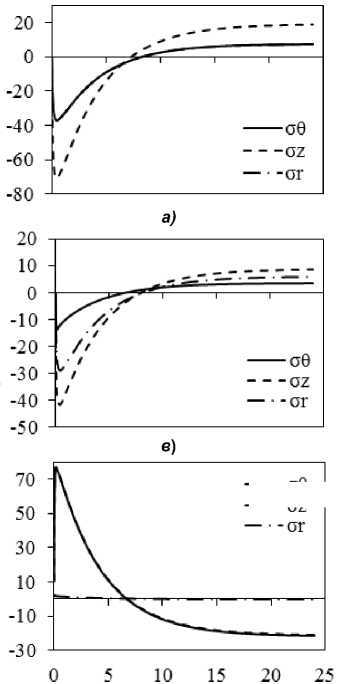
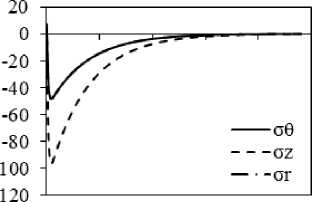
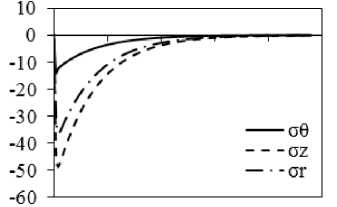
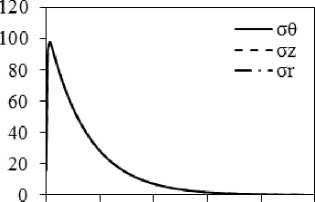
  Рис. 3. Результаты расчета внутренних напряжений при охлаждении на воздухе поковки диаметром 450 мм с учетом ( а, в, д, ж ) и без учета релаксации ( б, г, е, з ): а, б – через 0,5 ч; в, г – через 5 ч; д, е – через 7 ч; ж, з – через 15 ч после начала охлаждения

  
  

  С учётом релаксации

  

  д)

  
  

  Без учета релаксации

  
  
  

  б)

  
  
  

  ---О0 ---177

  
  

  г )

  

  О 5    10   15   20   25

  е)

  
  

  Время, ч

  
  

Рис. 4. Результаты расчета внутренних напряжений при охлаждении на воздухе поковки диаметром 450 мм в зависимости от длительности охлаждения с учетом (а, в, д) и без учета релаксации (б, г, е): а, б – на оси; в, г – в середине радиуса; д, е – на поверхности поковки щие) приведет к некоторому пластическому увеличению диаметра, а релаксация в осевой зоне – к аналогичному уменьшению диаметра поковки в этих зонах. Поэтому в серединной зоне должно наблюдаться дополнительное растяжение вдоль r и θ.

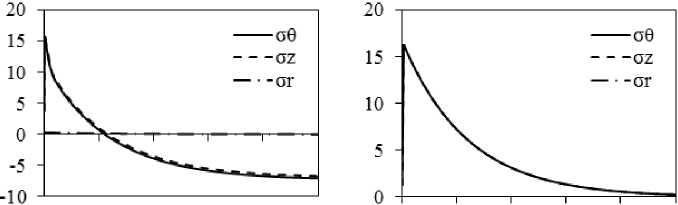
Расчет для поковки, охлаждающейся в течение 5 ч (рис. 3, в , г ), показывает, что график радиального изменения напряжений без учета релаксации принципиально сохраняет свой вид, но величины напряжений у оси и на поверхности уменьшаются в силу снижения разности температур между поверхностью и центром ( T п = 193 °С, T ц = 213 °С). В этом случае эффект релаксации приводит к уменьшению σ θ и σ z и в осевой, и в приповерхностной зонах. Вблизи r = R немного меняется характер изменения напряжений. Вместо восходящего участка появляется практически горизонтальный участок (рис. 3, в ).

Для 7-часового охлаждения (рис. 3, д ) характерно отчетливое формирование трех зон вдоль радиуса поковки. Дальнейшее уменьшение разности температур поверхности и центра ( T п = 129 °С, T ц = 142 °С) снижает термические напряжения.

С учётом релаксации                 Без учета релаксации

а)                                                 б)

в )                                                          г )

О 20   40   60   80   100      0    20   40   60   80   100

д)                                                 е)

Время, ч

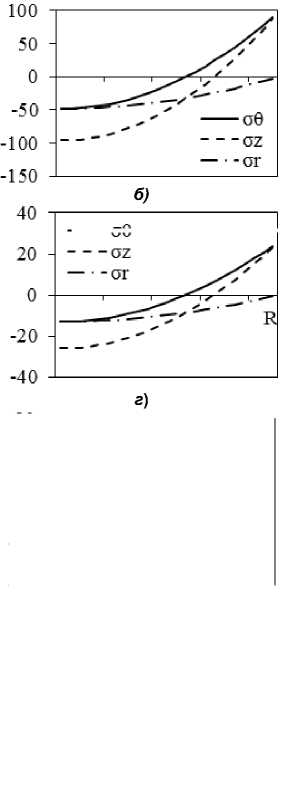
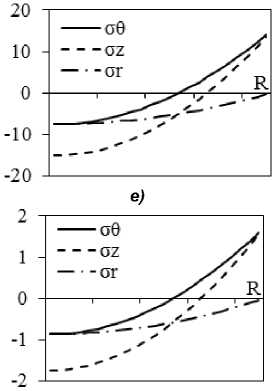
Рис. 5. Результаты расчета внутренних напряжений при замедленном охлаждении поковки диаметром 450 мм в зависимости от длительности охлаждения с учетом ( а, в, д ) и без учета релаксации ( б, г, е ): а, б – на оси; в, г – в середине радиуса; д, е – на поверхности поковки

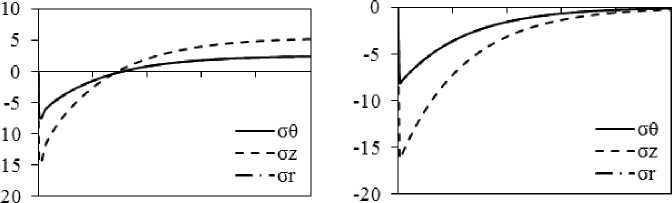
А поскольку поверхность образца из-за релаксации была увеличена, то теперь охлаждающаяся серединная зона начинает создавать в поверхностных слоях сжимающие напряжения σ θ . Кривые напряжений, при расчете которых релаксация не учитывалась (рис. 3, е ), по-прежнему отражают растягивающие напряжения у поверхности и сжимающие напряжения на оси. В данном случае видно, что σ_θ и σ _r определяются разностью температур поверхности и центра.

После 15-часового охлаждения отчетливо наблюдается (рис. 3, ж ) возникновение около оси поковок растягивающих напряжений σ θ , σ z и σ r , а у поверхности – сжимающих напряжений σ_θ и σ _z , величина которых достигает 20 МПа. Расчет в варианте отсутствия релаксаций (рис. 3, з ) дает ~ 1,5 МПа на поверхности и ~ 2 МПа у оси.

Более подробно временной характер изменения напряжений σθ, σz и σr на оси, при r = 1/2R и у поверхности представлены на рис. 4 с учетом релаксации и без неё. Общий характер изменения напряжений оказывается следующим: в отсутствие релаксации напряжения у поверхности растяги- вающие, а напряжения при r = 1/2R и на оси – сжимающие. Причем в первых двух случаях (рис. 4, б, г) их графики проходят через минимум и затем начинают возрастать по модулю асимптотически, приближаясь к 0 при продолжении охлаждения. Аналогично и на поверхности, пройдя через максимум, σθ и σz уменьшаются до 0 при дальнейшем охлаждении. При учете релаксации (рис. 4, а, в, д) наблюдается, во-первых, уменьшение уровня всех напряжений, может быть, за исключением очень малых времен охлаждения, причем при времени охлаждения более 7 ч графики напряжений пересекают 0 и, по существу, напряжения превращаются в остаточные напряжения растяжения около оси и сжатия у поверхности. Аналогично и для r=1/2R . При этом сжимающие напряжения будут препятствовать образованию флокенов, в которых трещина перпендикулярна действующему напряжению. Во-вторых, следует учитывать, что сжимающие напряжения вдоль θ и z будут препятствовать образованию флокенов, плоскость которых перпендикулярна этим напряжениям, поэтому поверхность возникающего флокена должна быть ориентирована перпендикулярно к радиусу, что в действительности довольно часто наблюдается в производстве и отмечается в публикациях [8].

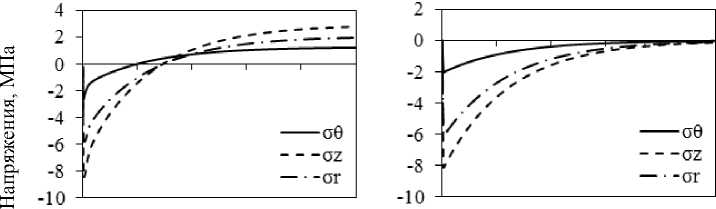
Рассмотренные выше графики внутренних напряжений относились к охлаждению поковки диаметром 450 мм на воздухе. Теперь рассмотрим случай, когда поковки охлаждаются замедленно со скоростью ~ 13 °С/ч, что примерно соответствует скорости охлаждения поковки в термосе [9]. Зависимость внутренних напряжений от времени охлаждения в двух вариантах (с учетом и без учета релаксации напряжений) представлены на рис. 5. Характер изменения напряжений оказывается таким, как и в решении, рассмотренном в случае охлаждения на воздухе (см. рис. 4). В отсутствие релаксации сохраняется общий характер изменения напряжений по радиусу и по времени, но все напряжения оказываются существенно меньшими (рис. 5, б , г , е ). В случае учета релаксации характер изменения напряжений также не меняется, но величина остаточных напряжений после охлаждения снижается приблизительно в 3 раза (рис. 5, а , в , д ).

С точки зрения возможности образования наличие на поверхности сжимающих напряжений препятствует образованию флокенов. Также можно предположить, что сжимающие напряжения препятствуют диффузионному выходу водорода в атмосферу. Влияние внешних напряжений на диффузию обычно сводят к уменьшению энергии активации диффузии на величину σVM , где σ – гидростатическое напряжение, равное

_{σ =} σ _r +σ_θ+σ _z 3

.

Поэтому в выражении для коэффициента диффузии водорода появляется дополнительный сомножитель

• - Q σ V_М

DH=D0eRTeRT , (4) то есть энергия активации заменяется на Q → Q - σVМ , где VМ – парциальный молярный объем растворенного водорода, который оценивается в 2 см3/моль. Если максимальное значение σ при охлаждении на воздухе у поверхности оцени- вается (см. рис. 3, ж)

- 20 - 20 + 0

- 13,3 МПа,

то дополнительный множитель, отражающий эффект уменьшения диффузии, будет равен σ V_М       - 13,3 ⋅ 10 ⁶ ⋅ 2 ⋅ 10 ^{- 6}

e RT = e 8,314⋅300   = 0,99 , то есть влияние напря жений на диффузию водорода пренебрежимо мало.

Однако на самой поверхности водород, по-видимому, удаляется ещё в процессе термической обработки слитков, нагрева под ковку, самой ковки и охлаждения после неё, так как при ковке про- исходит деформация с последующей рекристаллизацией, а прохождение большеугловых границ существенно увеличивает скорость диффузии водорода.

Выводы

• 1.    При охлаждении цилиндрических поковок в однофазной α-области возникают осевые ( σ _z ), радиальные ( σ r ), и тангенциальные ( σ θ ) напряжения. Если при аналитическом расчете без учета релаксации абсолютная величина напряжений уменьшается и стремится к нулю при подходе к комнатной температуре, то расчет с учетом релаксации внутренних напряжений показывает, что после окончания охлаждения в поковке сохраняются остаточные напряжения, причем на поверхности они сжимающие, а в центре поковки растягивающие.

• 2.    Наличие на поверхности сжимающих напряжений препятствует раскрытию флокенов.

• 3.    Показано, что влияние внутренних напряжений на диффузию водорода пренебрежимо мало.

Работа выполнена в рамках государственного задания Минобрнауки РФ и частично поддержана грантом РФФИ 14-03-00618.