Анализ точности шести формул для расчета оптической силы интраокулярных линз на глазах с аксиальной длиной 20-22 мм.

¹ Введение. В настоящее время точность рефракционных процедур признается одним из основных требований к хирургии катаракты, что достигается за счет попадания в целевую рефракцию в послеоперационном периоде. Развитие как инструментальной базы для выполнения более точных хирургических вмешательств, так и математических подходов к более точному предоперационному расчету представляется, по мнению исследователей, ключевым условием для достижения желаемого рефракционного результата у пациентов после удаления катаракты или прозрачного хрусталика [1].

Преломляющая способность прооперированного глаза в целом зависит от рефракции роговицы и хрусталика, аксиальной длины глаза и расположения ИОЛ [2]. Все указанные факторы играют значимую роль в достижении функциональных результатов в послеоперационном периоде [3–5]. Для глаз с нормальной аксиальной длиной (22– 24 мм) представлен целый ряд формул для расчета оптической силы ИОЛ, включая формулы третьего поколения, однако при наличии аксиальной длины более 24 мм или менее 22 мм попадание в послеоперационную рефракцию представляется затруднительным [1, 3, 6].

Цель: сравнительный анализ точности расчета оптической силы ИОЛ у пациентов с длиной глаза в диапазоне от 20 до 22 и от 22 до 24 мм.

Материал и методы. В исследовании участвовали 104 пациента (147 глаз). В опытную группу (I) включены 56 пациентов (81 глаз) с короткой передне-задней осью от 20,02 до 21,98 мм (21,17±0,56), которым проведена факоэмульсификация катаракты, или удаление прозрачного хрусталика, с имплантацией ИОЛ. Мужчины составили 44,7% (n=25), женщины 55,3% (n=31). Возрастной диапазон: от 36 до 88 лет (62,3±13,7 года).

В группу II (сравнения) вошли 48 пациентов (66 глаз) с нормальной аксиальной длиной 22,75±0,46 (22,0–23,77) мм с имплантацией различных моделей ИОЛ. Женщины составили 60,4% (n=29), мужчины 39,6% (n=19), возраст от 33 до 84 лет (68,6±9,7 года).

Всем пациентам проводили как стандартное (авторефрактометрия, тонометрия, визометрия, компьютерная периметрия, биомикроскопия, офтальмоскопия в условиях максимального мидриаза), так и специальное (кератотопография, эхография, ультразвуковая пахиметрия, оптическая когерентная

биометрия с определением аксиальной длины глаза, глубины передней камеры и кривизны роговицы, по показаниям — оптическая когерентная томография) офтальмологическое обследование.

Статистически значимых различий между группами в предоперационном периоде не выявлено, за исключением аксиальной длины глазного яблока и сферического компонента рефракции (3,2 дптр в группе I против –0,4 дптр в группе II, p<0,05).

Факоэмульсификацию катаракты и удаление прозрачного хрусталика с имплантацией различных мо-нофокальных ИОЛ (Alcon, США) выполняли по стандартной методике. Проводили ретроспективный расчет эффективности формул Hoffer-Q, Holladay 2, SRK/T, Olsen, Haigis и Barrett Universal II. Точность каждой из формул рассчитывали, сравнивая различие между целевым и расчетным SE (в идеале равное нулю) через 6 месяцев после хирургического вмешательства. Анализ осуществляли с помощью программного обеспечения системы VERION© и открытых данных на сайтах исследуемых формул. Период наблюдения пациентов составил 13,0±2,7 (6-72) месяца.

Статистическую обработку результатов проводили с применением компьютерных программ Microsoft Excel 2010 (Miscrosoft corp., США) и Statistica 10.1 (StatSoft, США). Рассчитывали среднее арифметическое значение (M), стандартное отклонение от него (SD), минимальные и максимальные значения. При оценке значимости различий результатов применяли t-критерий Стьюдента. Для сравнения частоты встречаемости признака применяли точный критерий Фишера. Доверительный интервал составил 95% при значимости на уровне тенденции 90%. Отклонение расчетного значения сферического эквивалента от целевого определяли с помощью дисперсионного анализа (ANOVA) и регрессионного анализа, при этом проводили ретроспективное сравнение отклонения сферического эквивалента при использовании различных формул для расчета ИОЛ. Для оценки различий средних погрешностей применяли тест Kruskal Wallis. Погрешность оценки (E) определяли как разницу между фактической послеоперационной SE в течение шести месяцев наблюдения и прогнозируемой послеоперационной SE. Абсолютную погрешность (AE) определяли как абсолютное значение E. Среднее значение AE рассчитывали для каждой формулы. Различия в средней AE для шести формул были проанализированы; кроме того, оценивали процент глаз с АЕ в пределах ±0,50 и ±1,0 дптр для каждой формулы.

Таблица 1

Анализ эффективности формул для расчета оптической силы интраокулярных линз для глаз с аксиальной длиной 20,0–22,0 мм

Значение	Holladay 2	Hoffer-Q	Haigis	SRK/T	Olsen	Barrett Universal II
Средняя погрешность оценки (дптр) ±SD	0,19±0,14	0,23±0,08	0,11±0,02	0,15±0,09	0,21±0,13	0,17±0,21
Диапазон погрешности	от –0,14	от –0,32	от –0,12	от –0,16	от –0,24	от –0,18
оценки (дптр)	до +0,65	до +0,47	до +0,36	до +0,55	до +0,71	до +0,46
Средняя абсолютная погрешность (дптр) ±SD	0,23±0,06	0,16±0,11	0,08±0,02	0,19±0,09	0,24±0,13	0,18±0,05
Диапазон абсолютной погрешности (дптр)	от 0,01 до 0,78	от 0,01 до 0,59	от 0,00 до 0,29	от 0,02 до 0,43	от 0,02 до 1,61	от 0,01 до 0,32
Медианная абсолютная погрешность (дптр)	0,28	0,24	0,14	0,30	0,32	0,22

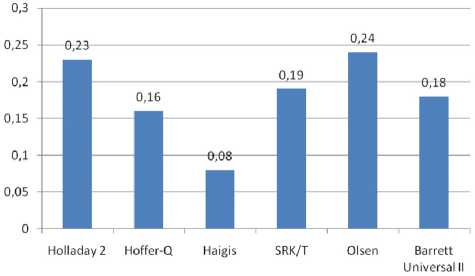
Рис. 1. Усредненные значения средней абсолютной погрешности для шести используемых формул в группе I

Таблица 2

Сравнений средних величин абсолютной погрешности в группе I

Сравнение MAE	Значение p (тест Kruskal Wallis)
Holladay 2/Hoffer-Q	>0,05
Holladay 2/Haigis	<0,05
Holladay 2/SRK/T	>0,05
Holladay 2/Olsen	>0,05
Holladay 2/Barrett Universal II	>0,05
Hoffer-Q/Haigis	0,05
Hoffer-Q/SRK/T	>0,05
Hoffer-Q/Olsen	>0,05
Hoffer-Q/Barrett Universal II	>0,05
Haigis/SRK/T	0,05
Haigis/Olsen	<0,05**
Haigis/Barrett Universal II	0,05
SRK/T/Olsen	>0,05
SRK/T/Barrett Universal II	>0,05
Olsen/Barrett Universal II	>0,05

П р и м еч а н и е : * — различия значимы на уровне тенденции;

** — различия статистически значимы.

Результаты. Результаты статистического анализа в группе I представлены в табл. 1.

Группа характеризовалась статистически незначимыми (p<0,05) различиями в средней погрешно сти оценки для формул Holladay 2, Hoffer-Q, SRK/T, Olsen и Barrett Universal II (0,19±0,14; 0,23±0,08; 0,15±0,09; 0,21±0,13 и 0,17±0,21 дптр соответственно). Вместе с тем при использовании формулы Haigis получена наименьшая средняя погрешность оценки (0,11±0,02), различия значимы на уровне тенденции (0,05

Процент глаз с AE в пределах ±0,50 дптр для формул Holladay 2, Hoffer-Q, Haigis, SRK/T, Olsen и Barrett Universal II составил 79,0, 81,5, 93,4, 88,9, 80,2 и 92,5% соответственно; в пределах ±1,00 дптр — 97,5, 100, 100, 100, 93,4 и 100% соответственно.

После расчета средних значений проведен попарный анализ с учетом каждой из исследуемых формул (табл. 2).

Проведенный сравнительный анализ показал значимое (p<0,05) преимущество формулы Hagis по сравнению с Holladay 2 и Olsen, а также значимое на уровне тенденции (0,05

0,05).

Схожий анализ представлен по группе II (сравнения) для глаз с аксиальной длиной 22,0–24,0 мм (табл. 3).

В отличие от группы I, в группе II различий между формулами Holladay 2, Hoffer-Q, Haigis, SRK/T, Olsen и Barrett Universal II при оценке средней погрешности не выявлено (0,10±0,12; 0,08±0,19; 0,02±0,05; 0,13±0,09; 0,11±0,04 и 0,06±0,10 соответственно). Схожие данные определены и для средней абсолютной погрешности (0,23±0,09; 0,29±0,13; 0,15±0,06; 0,19±0,12; 0,16±0,04 и 0,12±0,08 соответственно) (рис. 2), что свидетельствует о сопоставимой эффективности всех исследуемых формул для расчета оптической силы ИОЛ у пациентов с нормальной аксиальной длиной.

Процент глаз с AE в пределах ±0,50 дптр для формул Holladay 2, Hoffer-Q, Haigis, SRK/T, Olsen и Barrett Universal II составил 100, 97, 100,100,100 и 100 соответственно, в пределах ±1,00 дптр — 100% для всех исследуемых формул.

Таблица 3

Анализ эффективности формул для расчета оптической силы интраокулярных линз для глаз с нормальной аксиальной длиной

Значение	Holladay 2	Hoffer-Q	Haigis	SRK/T	Olsen	Barrett Universal II
Средняя погрешность оценки (дптр) ±SD	0,10±0,12	0,08±0,19	0,02±0,05	0,13±0,09	0,11±0,04	0,06±0,10
Диапазон погрешности	от –0,25	от –0,19	от –0,14	от –0,26	от –0,21	от –0,20
оценки (дптр)	до +0,22	до +0,28	до +0,17	до +0,40	до +0,32	до +0,23
Средняя абсолютная погрешность (дптр) ±SD	0,23±0,09	0,29±0,13	0,15±0,06	0,19±0,12	0,16±0,04	0,12±0,08
Диапазон абсолютной погрешности (дптр)	от 0,00 до 0,41	от 0,00 до 0,53	от 0,00 до 0,40	от 0,00 до 0,45	от 0,00 до 0,38	от 0,00 до 0,33
Медианная абсолютная погрешность (дптр)	0,20	0,22	0,19	0,12	0,12	0,10

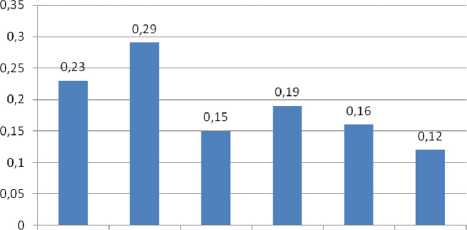
Holladay2 Hoffer-Q Haigis SRK/T Olsen Barrett

Universal II

Рис. 2. Усредненные значения средней абсолютной погрешности для шести используемых формул в группе II

При проведении попарного анализа значимых различий между исследуемыми формулами не выявлено (p>0,05 во всех случаях).

Обсуждение. Выбор адекватной формулы для расчета оптической силы ИОЛ на коротких глазах остается актуальной проблемой офтальмохирургии. G. Carifi с соавт. изучали особенности расчета оптической силы ИОЛ на 28 глазах с короткой передне-задней осью и пришли к выводу об отсутствии значимых различий между исследуемыми формулами, однако несколько лучшие значения получены для формул Hoffer-Q, Haigis и Holladay 2 [7]. В нашей работе значимых отличий при проведении сравнительного анализа не выявлено, однако попарный анализ показал некоторое преимущество формулы Haigis для глаз с аксиальной длиной 20–22 мм.

В работе E.A. Gavin и С. J. Hammond показано, что формула Hoffer-Q обладает преимуществом по сравнению с SRK/T для глаз с аксиальной длиной 20–22 мм [1]. Мы не подтвердили данные результаты в собственном исследовании.

D. Doshi и соавт. заключили, что формулы Hoffer-Q, Holladay 1 и SRK/T одинаково эффективны для глаз с короткой переднее-задней осью, а точность указанных формул была выше, чем формулы Haigis [8]. Напротив, M. M. Moschos и соавт. показали, что формула Haigis точнее по сравнению с Hoffer-Q, Holladay 1 и SRK/T в прогнозировании послеоперационной рефракции [3]. В двух указанных работах для измерения основных параметров применяли иммерсионное ультразвуковое исследование. В нашей работе получены схожие с M. M. Moschos и соавт. данные о некотором преимуществе формулы Haigis, при этом мы изучали формулу Holladay 2, а не Holladay 1.

J. X. Kane с соавт. изучали 156 коротких глаз и не выявили значимых различий между формулами Barrett Universal II, Haigis, Hoffer-Q, Holladay 1, Holladay 2, SRK/T и -T2 [9]. В своей работе авторы не следовали рекомендациям K. J. Hoffer и соавт. [10] о предпочтительном сопоставлении средней абсолютной погрешности, а не медианной абсолютной погрешности и об оценке рефракции через 14 дней после хирургического вмешательства. J. X. Kane и соавт. не проводили также измерение толщины хрусталика. Работа S. E. Gokce и соавт. включала 86 глаз с короткой переднее-задней осью, при этом сравнение проводили с использованием формул Barrett Universal II, Haigis, RBF, Hoffer-Q, Holladay 1, Holladay 2 и Olsen. Значимых различий между формулами выявлено не было [11]. В наше исследование включены формулы Barrett Universal II, Haigis, Hoffer-Q, Holladay 2, SRK/T и Olsen, при этом показано некоторое преимущество формулы Haigis.

Заключение. Итак, представлены результаты исследования шести формул, применяемых при расчете оптической силы ИОЛ, для глаз с длиной в диапазоне от 20 до 22 мм. Показано преимущество применения формулы Haigis для достижения оптимальной целевой рефракции. В группе пациентов с нормальной аксиальной длиной статистически значимых различий между исследуемыми формулами не выявлено.