Анализ управляемости и устойчивости приближенной модели теплопереноса в автоклаве

Начиная с работ Б. Е. Щекина1 и Е. В. Выскубова [1] принято описывать процесс нагрева воды паром в авто- клаве, в который помещены банки со стерилизуемым продуктом, как динамический процесс в приращениях с сосредоточенными параметрами. Ис- ходя из уравнений сохранения энергии и теплопроводности Фурье2 для сосредоточенной системы при управлении тепловым потоком пара Qn и потерей тепла на нагрев банок q6 выходные координаты процесса температура воды 0в и температура банок 0б (при неизменном давлении в автоклаве и без учета потерь на нагрев охлаждающей воды, корпуса и в окружающую среду) запишем в виде системы двух обыкновенных дифференциальных уравнений первого порядка:

т с d®8 = 0 -а • meCe dt    Qn Чб;

d ®б m'

= ^a e6 F 6 ( ® _в ^-® б ) , ⁽¹⁾

где m_в , m_б , С_в , С_б – масса и удельная теплоемкость воды и банок соответственно; а_вб - коэффициент теплопроводности вода-банка; F_б – площадь внешних поверхностей всех банок.

Эффективность процессов стерилизации по производительности и качеству по соответствию траекторий процесса заданной формуле стерилизации, учитывающей зависимость температуры воды 0в от времени, определяется системой управления процессом. Для систем управления автоклавами, как и для других систем управления реальными объектами, справедливо утверждение [2], что в 2000–2010-е гг. «… овершенствование автоматических систем базировалось на развитии технических средств автоматики, основанном на достижениях в области электроники, приборостроения, вычислительной техники и мехатроники, а теоретическая база систем автоматического управления слабо развивалась». Исходя из этого утверждения, авторы данной работы сделали попытку обосновать принимаемые технические решения реализации систем управления автоклавами с позиций фундаментальных свойств управляемости и устойчивости3 систем управления в зависимости от структурно-функциональных особенностей объекта управления, определяемых его параметрами и связями.

Обзор литературы

Аппаратная реализация аналоговых систем управления процессами стерилизации известна из работы Б. Е. Щекина4. Аппаратные реализации цифровых алгоритмов классических законов регулирования (релейного, скользящего и пропорционально-интегральнодифференциального (ПИД) законов) в системах управления автоклавами с помощью элементов микроДАТ заложены в исследовании Е. В. Выскубова5 и обобщены в справочнике В. П. Баба-рина6. Развитие программно-аппаратных систем управления автоклавами началось с работы С. А. Мокрушина [3] и продолжено в работах [4–7].

С теоретической точки зрения интерес представляет работа Е. В. Выску-бова7 об оптимальном управлении процессом (1), в которой автор, ссылаясь на правило А. Ю. Ишлинского8 для достаточности двумерной модели (1), находит с помощью принципа макси- и мума Л. С. Понтрягина9 качественные решения оптимального управления, т. е. в каких функциях искать управление в задаче быстродействия и в задаче программного движения (в последней – не учитывая нелинейность, явное вхождение времени в функционал и особые в смысле принципа максимума режимы, а также качественные свойства модели по управляемости и устойчивости). В работе О. М. Клименко и В. Г. Трегуба [8] предложен нейронный метод управления автоклавом, но он основан на программно-аппаратной реализации по структуре системы С. А. Мокрушина [3] и формуле стерилизации «нагрев-выдержка-охла-ждение».

В зарубежной научной литературе существуют примеры аппаратной [9], программно-аппаратной10 и нейронной [10] реализаций систем управления автоклавами. Основное внимание в перечисленных работах уделено техническим средствам реализации системы управления, но не исследовано влияние параметров модели на алгоритм управления.

Том 28, № 3. 2018

Материалы и методы

Исходя из цели исследования в работе решаются задачи:

• 1 ) качественного анализа управляемости по Калману¹¹ приближенной модели (1) в пространстве состояний (отдельно показан переход от передаточной функции с нулями в числителе к нормальной системе дифференциальных уравнений в форме Коши, опирающийся на исследование В. С. Хорошавина, А. В. Зотова и С. А. Мокрушина [11]);

• 2 ) качественного анализа устойчивости приближенной модели (1) с помощью передаточных функций и структурных преобразований, соотношения параметров процесса в виде неравенств¹² и последующим выбором составляющих ПИД-закона регулирования [12] для реального автоклава¹³ с помощью матрицы экспертных оценок¹⁴.

Результаты исследования

Анализ управляемости процесса

Структурная схема приближенной модели (1) при замене символа дифференцирования на оператор Лапласа dt p представлена на рис. 1.

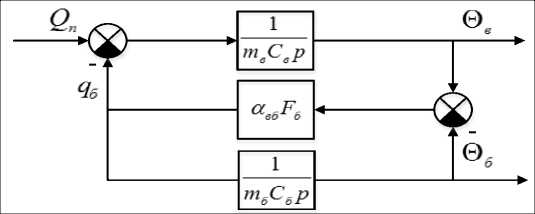
Р и с. 1. Структурная схема приближенной модели (1)

F i g. 1. Block diagram of approximate model (1)

В формулах стерилизации¹⁵ указывается температура греющей среды Θ _в , которую нужно измерить в замкнутой системе управления, например, с ПИД-регулятором, поэтому запишем передаточную функцию объекта управления как замкнутой системы с выходом Θ _в и входом Q_n по модели (1):

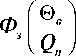
__________ ^m6 C₆P + ^a e6 F 6 __________

Р 2 ( ^m _eC_em 6^C6 ) + Pa₈ 6 F 6 ( mC + ^m6 C 6 ) ^.

Для анализа управляемости передаточной функции (2) потребуется переход от передаточной функции с нулями в числителе в пространство состояний без производных по управлению Qn. Такой переход возможен путем понижения старшей производной 0в и вве- дения дополнительных сигналов по управлению Qn, учитывающих производные по управлению Qn. Здесь и да- лее для краткости записи производных от переменных обозначим, например, dx

x =     .

dt

Поскольку такой переход обычно вызывает затруднения [11], то в мето- дическом плане покажем пошаговую процедуру его применения на примере.

Известно, что представление динамики процесса с передаточной функцией без нулей в числителе в пространство состояний не вызывает трудностей при понижении порядка старшей производной выхода.

Далее, более кратко по сравнению с приведенным в [11], формализуем процедуру представления передаточной функции с нулями в пространство состояний на примере объекта

I

X + T0 x = k0U + k1U     (3)

со структурой, представленной на рис. 2.

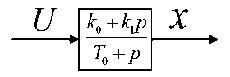
Р и с. 2. Структура исходного объекта (3) с нулями в числителе

F i g. 2. Diagram of the original object (3) with zeros in the numerator

В уравнении (3) объекта (рис. 2) примем коэффициент при старшей производной выхода равным 1.

• 1    шаг. Введем дополнительные переменные

x = x 1 + h0U,

X1 = x - h0U = x2 + h1U и т. д. до xn -1 = xn + hn -1U.

• 2    шаг. Подставим введенные дополнительные переменные в исходное уравнение:

Х1 + h0U = k0U + k1U - T0 (x 1 + h0U).

• 3    шаг. Избавимся от производных по U в последнем уравнении:

x1 = k0U + k111 - h^ IU - T,x 1 - T,hU, I    ki)

(л h )

из 1 1 - 0 I = 0 получим h 0 = k 1 . Тогда

I    k\)

система уравнений объекта и его структура в пространстве состояний примут следующий вид (рис. 3):

JC1 = U(k0 - kT0)- T0X,;

x = x 1 + k1U.

Из приведенного простейшего примера видна сложность метода понижения порядка старшей производной вы-

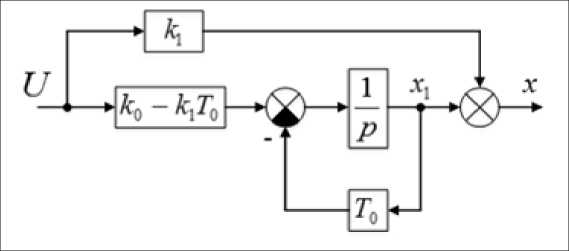
Р и с. 3. Структура исходного объекта (3) без нулей в числителе

F i g. 3. Diagram of the source object (3) without zeros in the numerator

хода и введения добавок по управлению, учитывающих производные по управлению, хотя новая структура (рис. 3) позволяет более детально оценить влияние параметров в исходной структуре (рис. 2).

Для анализа управляемости модели (1) со структурой на рис. 1 с целью исключения производных по управлению воспользуемся правилами преобразования структурных схем для получения передаточной функции с выходом Θ _б , более точно отражающим качество процесса по сравнению с Θ _в , для чего перенесем точку съема сигнала q_б на сигнал Θ _б (рис. 4).

На основании данной структурной модели запишем передаточную функцию:

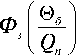
a _e6 ^F6

Р2 (mCmeC) + P«e6F6 (meCe + m6C6), которая путем понижения порядка старшей производной Θб может быть преобразована к нормальной системе дифференциальных уравнений первого

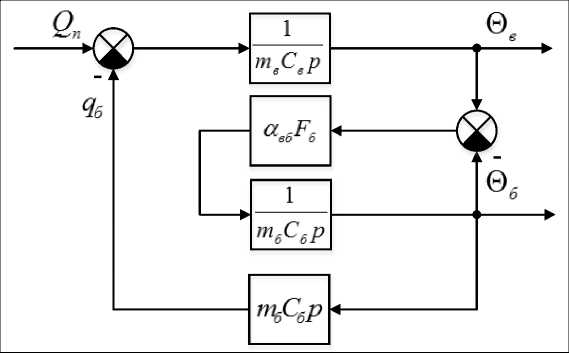
Р и с. 4. Преобразованная структурная схема модели (1)

F i g. 4. Transformed block diagram of the model (1)

порядка, что и требуется для исследования управляемости по Калману.

В нормальной форме Коши передаточной функции (4) путем понижения порядка производной Θ _б поставим в соответствие следующую систему с управлением U = Q_n :

I

^Х 2

X = X 2 ,     X 1 =0 ₆,    X = 0 ₆,

“ ^s6 ^ ⁶ U - aF [ — + —) х ₂;

тСт б С б     ^{86 6} 1 mC  m 6 C 6 J 2

или в матричной форме x = Ax + BU, для которой матрица управляемости D 2 = ( B AB )имеет вид

D 2 =

^a e6 F 6

I т_вС_вт_бС_б

^F6

^m« C «^m6 C 6

a F ) 2 Г 1 + 1 ) ^m _eC_e ^m6 C 6 1 ^{mC m}6 C 6 Jj

Определитель матрицы D ₂ не равен нулю:

_     1     a . F „     1

det D_? = ---- ^{55 5}      * 0, (6)

2       \                             i

V m e e^m6 5 )

т. е. система полностью управляема.

Однако такой путь по правилам преобразования структурных схем не является формализованным, поскольку трудно в общем случае указать правила преобразования исходной структуры (рис. 1) к виду, удобному для исследования управляемости модели (1).

Ранее для исследования управляемости модели (1) мы пытались преобразовать ее к нормальной системе дифференциальных уравнений в форме Коши, что вызывало значительные затруднения. Хотя модель (1) не является нормальной формой Коши, это не является ограничением для применения условий управляемости Калмана. В результате получим, что система (1) является полностью управляемой.

Из анализа матрицы управляемости процесса, например, из det D 2 (6) следует, что степень управляемости системы повышается с увеличением теплопере-носа от воды к банкам ( a_e6F₆ ) и уменьшением инерционности нагрева воды и банок ( т₆С в т_бС б ), что физически объяснимо.

Анализ устойчивости процесса

Используя полученные при исследовании управляемости передаточные функции (2; 4) и уравнения состояний во временной области (5), найдем полюса передаточных функций, или характеристические корни:

А = 0,     Я 2 = ^-a _e6F₆

m e^Ce ⁺ m 6^C6 ^me^Ce m 6 C 6

< 0

из которых следует, что система обладает интегрирующими свойствами, т. е. не имеет самовыравнивания [12] и находится на грани устойчивости.

Вообще говоря, из эквивалентных структурных схем (рис. 1 и рис. 4) видно, что «успокоить» процесс нагрева воды паром могут потери на нагрев банок и другие потери. Рассмотрим, как влияют потери на нагрев банок, т. е. загрузка автоклава, которые являются основными по технологии стерилизации, на передаточные функции системы.

Рассмотрим передаточную функцию преобразования 0 в в 0 б по структуре, приведенной на рис. 4. Передаточная функция замкнутого контура равна

ф f^L)=   *___= -d-,

31 0 J m6C6     ,   T, p +1

в О     p + 1      6e^p

ae6F6

что является передаточной функцией апериодического звена с постоянной времени нагрева банок водой

T

6e

^a e6^F6

Что касается соотношения массы банок и площади их поверхности в последней формуле для постоянной времени нагрева банок водой, то поскольку масса банок определяется произведением плотности содержимого банок на их объем, величина Т бв зависит от соотношения объема и площади банок. Из геометрии плоских фигур и тел извест-но¹⁶, что для выпуклых многогранников, (т. е. таких форм контейнеров, как куб, параллелепипед, цилиндр), в которые помещаются банки, соотношение объе-

с постоянной времени Т_бв ,

ма к площади прямо пропорционально параметрам многогранника. Поэтому говоря о загрузке автоклава, будем подразумевать прямую зависимость постоянной времени T_бв и массы банок.

При малой загрузке Т бв <<  1 получим почти усилительное звено (апери-

характеризующей загрузку автоклава m_б с некоторыми приведенными выше оговорками относительно связи т б и F_б , удобнее использовать структуру, представленную на рис. 4, т. к. в структуре рис. 1 придется выделить допол-

Г©^

нительно из Ф - промежуточный ³ 1© в )

сигнал q6 с дифференциальной составляющей тбСб p, которая, кстати, улучшает устойчивость процесса. Исполь-Г®Л зуя структуру рис. 4 с учетом Ф3I I, получим:                     к®«У

одическое звено с широкой полосой

( 0

Ф —

³ 1g

X ^ П

meCeP + твСбРф3

пропускания) Ф_з

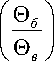
1, при боль

® 5 ® в

.

шой загрузке Т бв >> 1 получим интег-

Г ©Л    1 тг рирующее звено Ф - ®---. Для

31®в )  Т6вР нормальных (штатных) загрузок автоклава Б6-КАВ-217 по технологической

Воспользовавшись результатами

исследований [12], получим, что при

( ®„ малой загрузке Ф -³ \®„

Г®.)         1

карте стерилизации [1] с параметрами

meCeP + msCsP

« 1, тогда

- интегри-

m6C6 = 4,6 ■ 102 х 3,68 ■ 103

ae6F6 = 1,45 ■ 103 х 3,87 ■ 104

получим Т_6в » 30 c, Ф₃ одическое звено.

Дж град..

Дж с ■ град.

f®.) I®,)

-апери-

В дальнейшем для исследова-

рующее звено, а в системе регулирования с обратной связью с ПИД-регулятором достаточно пропорциональной составляющей с небольшими включениями интегральной и дифференциальной составляющих.

При большой загрузке

ф ©б ~  1  _ авб±б

31©в ) ТбвР   тбСбР ’ ф Гл ~_____1_____-

3 I Qn )  meCeP + «e6F6

ния устойчивости процесса с учетом введенной передаточной функции

инерционное звено; регулируется с помощью П-регулятора.

• ¹⁶    Korn G. A., Aramanovich I. G., Korn T. M. Mathematical handbook for scientists and engineers: definitions, theorems, and formulas for reference and review . Mineola ; New York : Dover Publications, 2000. 1130 p.

• ¹⁷    Вертикальные автоклавы Б6-КАВ-2 / Б6-КАВ-4 . 2012.

При нормальной загрузке получим Г© J объект с Ф I5  (1), имеющий реаль ное дифференцирующее, интегрирую- щее и апериодическое звенья, поэтому могут потребоваться в разной степени все составляющие ПИД-закона регулирования.

Предыдущие рассуждения по выбору составляющих ПИД-закона регулирования в зависимости от загрузки автоклава можно представить в виде матрицы экспертных оценок¹⁸. В данном случае она составляется для нормализованных весов j -тых составляющих ПИД-закона для каждой i -той 3

загрузки q ij , ^ q ij = 1 и нормализован- j = 1

ных весовых коэффициентов загрузки ^> , £ ^i = 1 (таблица).

i = 1

Для каждого j -того решения вычисляется показатель Rj как сумма произведений нормализованного веса j -того решения на соответствующий весовой коэффициент μ_i , причем показатели R_j получаются нормализованными: 3

^ R j = 1. Оптимальное решение опре- j =1

деляется по максимальному значению R_j . В таком случае наиболее целесообразно применять пропорциональную составляющую ПИД-закона регулирования.

Т а б л и ц а 1

T a b l e 1

Матрица экспертных оценок Matrix of expert opinions

Загрузка ( i ) / Load ( i )	Составляющие ( j ) ПИД-закона и соответствующие нормализованные веса q ij / Components j ') of the PID-law and the corresponding normalized weights qij			Вес коэффициента μ i / Weight of coefficient μi
	П / P	И / I	Д / D
Малая T бв << 1 с / Small Tбв << 1 sec	0,6	0,2	0,2	0,1
Нормальная T бв ≈ 30 с / Normal T бв ≈ 30 sec	0,5	0,4	0,1	0,7
Большая T бв >> 1 с / Big Tбв >> 1 sec	0,6	0,2	0,2	0,2
Показатель 3 R j = i Mj / i = 1 Indicator R = i ^ i = 1	0,53	0,34	0,13

¹⁸ Системный анализ и принятие решений : словарь-справочник / Под ред. В. Н. Волковой, В. Н. Козлова. М. : Высшая школа. 2004.

Обсуждение и заключения

Для качественного исследования вопросов управляемости и устойчивости приближенной модели теплового процесса нагрева воды паром в автоклаве в зависимости от параметров процесса необходимо совместное представление модели как во временной (в пространстве состояний), так и в частотной (в виде передаточных функций) областях с анализом соотношения параметров в виде неравенств. Для выбора регулятора процесса удобно применять матрицу экспертных оценок.

Результаты исследования послужат материалом для разработки реальной модели процесса автоклавирования с учетом статических и динамических характеристик измерительных, преобразовательных и исполнительных элементов, исследования влияния и компенсации инерционностей и нелинейностей реальных элементов с последующей разработкой автоматизированной системы управления процессом автоклавирования. Результаты работы могут быть использованы для исследования общих и прикладных проблем оптимального управления19 как в пищевой, так и в других отраслях промышленности, например, в производстве стройматериалов [13] и резинотехнических изделий [4; 9].

Поступила 06.02.2018; принята к публикации 02.04.2018; опубликована онлайн 20.09.2018

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

cyberleninka.ru/article/n/algoritmy-upravleniya-tehnologicheskim-protsessom-vulkanizatsii-ustanovki- avtoklav (In Russ.)