Анализ упругих деформаций, индуцированных гидридным превращением в магнии, в рамках градиентной теории упругости

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

Необходимость снижения парниковых газов в атмосфере, уменьшения выбросов СО 2 и диверсификация химических технологий с целью повышения эффективности производства требуют новых подходов к поиску и замене традиционных источников энергии на новые, с меньшим содержанием вредных выбросов. Подобная задача не имеет быстрого решения и требует комплексных исследований научных, инженерных и конструкторских коллективов. Водород является идеальным энергоносителем. Однако существующие на сегодня методы его хранения, такие как газ под высоким давлением или сжиженный водород, не могут соответствовать будущим целям его применения, прежде всего по безопасности. Металлогидридный способ хранения водорода лишен этого недостатка. В последнее время проводятся интенсивные исследования гидридов металлов с целью улучшения свойств и кинетики гидрирования [1–3].

Группа гидридов на основе Mg является многообещающим кандидатом для конкурентоспособного хранения водорода с обратимой водородной емкостью до 7,6 мас.% [4; 5]. Несмотря на то что первая промышлен- ная установка, основанная на металлогидридном способе хранения водорода [6], была произведена в 2012 г., вплоть до настоящего времени этот опыт не получил широкого распространения. Основная причина заключается в том, что масштабирование этого успешного эксперимента требует создания инфраструктуры, которая включает как само предложение, так и потребность его использования. Основным тормозящим фактором на этом пути является кинетика сорбции/десорбции водорода в магнии, на которую оказывают влияние различные факторы. Не последнее место среди них отводится напряжениям, возникающим в ходе гидридного превращения и инициирующим развитие как упругой, так и (в ряде случаев) пластической деформации. Существует общее представление, что такие напряжения при многократном повторении циклов «сорбция/десорбция водорода» приводят к изменению фракционного состава исходного материала, что оказывает влияние на обратимость процесса [7; 8].

Гидрид магния MgH2 представляет собой химическое соединение. Водород, проникая в магний в достаточном для образования гидрида количестве, провоцирует фазовый переход, который сопровождается изменением параметров элементарной ячейки. Вначале в металле под действием градиента концентрации водорода возникает градиент расширения кристаллической решетки металла, что приводит к появлению внутренних напряжений в структуре магния, индуцированных водородом. Такие напряжения называют концентрационными напряжениями, или водородоупругостью [9]. При возникновении устойчивого зародыша гидрида когерентная связь «гидрид – матрица» нарушается, и при разнице в объемах элементарных ячеек 30 % гидридный зародыш провоцирует появление упругих деформаций вокруг него. В процессе роста зародыша из-за этого же несоответствия объемов возможно развитие пластической деформации металла, которая сопровождается возникновением и ростом плотности дислокаций в матрице [10; 11].

Поскольку пластическая деформация в этом случае обусловлена фазовым (гидридным) превращением, иногда говорят о «водородофазовых» напряжениях [12]. Ряд авторов предполагает [13–17], что деформации в этом случае локализованы только вблизи гидрида и могут достигать значительной величины вплоть до разрушения материала. Задача еще более усложняется, если принять во внимание место зарождения гидрида (внутри матрицы, на свободной поверхности, ювенильной поверхности или в зоне роста трещины, на линии дислокации и т.д.). Одновременно учесть все возможные факторы, влияющие на кинетику роста новой фазы, практически невозможно, поэтому существует несколько моделей этого процесса [18]. Трудность проверки той или иной модели связана с тем, что они включают несколько элементарных физических механизмов.

В последние годы возрос интерес к расчетным методам исследования, которые позволяют выделить различные стадии возникновения и роста зародышей новой фазы [19–21]. Деформационное поведение материала в процессе гидридного превращения актуально и в качестве прототипа для моделирования зародышеобразования при фазовом переходе, а результаты расчетов для проверки можно соотнести с экспериментом. В качестве примера приведем работы [22; 23], где были предложены новые энергетические условия устойчивости механической системы «магний – гидрид магния», интерпретирующие появление новой фазы в напряженно-деформированном состоянии системы путем перехода к соответствующей термоупругой задаче. Авторами выявлены энергетически выгодные величины и формы зародышей в зависимости от физико-механических параметров системы. Дальнейшее развитие этого направления расчетов с новой формулировкой энергетических условий, а также оценка влияния близлежащих свободных поверхностей (полостей) или зародышей гидрида на величину полной энергии системы, представлено в работе [24].

В настоящее время интенсивно развиваются теории обобщенного континуума, использующие неклассические определяющие соотношения [25]. Это связано, прежде всего, с необходимостью описания размерных эффектов, в том числе в наноструктурированных материалах, различных сверхтонких структурах, материалах с большими градиентами неоднородностей, и другими задачами на мезо- и микроуровне [26]. Первоначальные идеи исходят к моделям братьев Коссера (1910), далее неклассические теории развивались в работах Тупина, Миндлина и других ученых [27–29].

На практике используются, как правило, упрощенные (прикладные) модели с малым количеством параметров, в частности, однопараметрические модели [30; 31]. Наиболее распространенной однопараметрической градиентной теорией упругости является вариант Ай-фантиса [32], который положен в основу расчетов, приведенных в данном исследовании. Основное внимание обращено на условия возникновения и распределения деформации, которая является неотъемлемой частью процесса фазового превращения, сопровождая образование зародыша гидрида магния. Это связано со следующими факторами. Во-первых, абсорбция водорода металлом на первом этапе его проникновения представляет собой градиентное распределение водорода вглубь исследуемого объекта. Во-вторых, на этом этапе распределение водорода неоднородно. Это подразумевает, что в локальных микрообъемах материала концентрация водорода превышает пороговые для диффузионного распределения значения, а в ряде случаев может достигать критического значения, достаточного для образования гидрида. Таким образом, описание возникновения и оценка уровня деформаций и напряжений в окрестности зародыша гидрида в рамках градиентной теории представляет исследовательский интерес. Статья посвящена изучению упругих деформаций, индуцированных образованием гидрида, анализу фазового превращения в слое при одноосной деформации и влиянию различных параметров на полную энергию системы в рамках градиентной теории упругости.

Постановка задачи

Общие соотношения . Простейший вариант градиентной теории упругости изотропного материала основывается на выражении плотности энергии упругой деформации w как функции деформации и ее градиента [32]

• 1,                       Г                          ^

w = 2 Ч- i ^s jj + ^s ij ^s j + l I 2 ^^ i^kk ^s jj,k + ^e _v, k ^s jk I , ⁽¹ )

где l – градиентный параметр, имеющий размерность длины.

Считается, что градиентная теория более подходит для описания упругого поведения материалов на микроуровне, причем параметр l имеет порядок характерного размера объекта, например, зерна.

Тензор малых деформаций определяется обычным образом s j = 2( ui, j + uj,.).                       (2)

Тензор напряжений Коши τij записывается обычным образом dw т ij = ЗГ’

Полные напряжения определяются как

° j = ^T у - mijk , к = (1- ¹ 2 ^{А ) т} у ,                 ⁽⁴⁾

d w    ,2

где mijk =----= l т^ к - компоненты тензора момент-St ij, k ных напряжений; ∆ – оператор Лапласа.

Уравнения равновесия формулируются для полных напряжений

° у,у + f. = 0,                       (5)

Физические уравнения (9) связывают напряжения Коши и моментные напряжения с упругими деформациями и деформациями фазового превращения при сделанном предположении.

Одноосная деформация слоя, состоящего из матрицы и гидрида. В области гидридного превращения выделим слой единичной толщины, который содержит магний и гидрид. Пусть координата x 1 = x направлена поперек слоя, тогда u = u 1 ( x ) , u ₂ = u ₃ = 0 .

Деформации выражаются как

5 u sx (x) = dx ~ £11 , s22

= ^s 33

0, ^s V   ^s i1 ^{+ s} 22 ^{+ s} 33     ^s x .

где f_i – компоненты вектора объемных сил.

В области фазового превращения (гидрида) полная деформация складывается из упругой части (1.1) s j и части, связанной с фазовым превращением s f

В области матрицы h≤x ≤1, где h – предельное значение зоны превращения (толщина слоя гидрида)

5 w

^T 11 = ^T x = a ^dsx

Xs V 5 11 + 2 цs ₁₁ = ( X + 2 ц ) £ 11 = ( X + 2 ц ) s x ,

^T 22

ef s ij s ij + s ij.

= ^T У

Мы предполагаем, что гидрид растет изотропно – одинаково по всем направлениям [24], поэтому s f = з s V 5 ij , где s V - объемная деформация при фазо-

^T 33

= ^T z

d w ^ds 22

d w ds ₃₃

= ^Xs V ⁵ 22 = ^Xs x ,

= ^Xs V ⁵ зз = ^Xs x ,

11 =^T 11    ^m 111,1 =^T 11 ^{l T}i

d ² s

= ( ^{X + 2} ц ) ^s x ^{- 1} 2 — x I ,

d x

вом превращении. Выразим из (6) упругие деформации s e и подставим их в плотность энергии упругой дефор-

° 22    ° 33 ^XI ^s x

1 2             |.

d x ² J

мации w (1), получим после преобразований

Уравнение равновесия (5)

f22          I wf = 2 X f(s V -s V’ + ^f к

^- 3 ^s V ⁵ j V ij

— 3 ^s V ⁵ j V"'

3s, ₂ d 3 s

—- - 1 ² — x = 0.

d x      d x ³

•••+ l f 1 2 ^x f ( ^s V , k -^s V , k ^{) 2} +

^{+ц f} I^s j , k 3 ^s Vk ⁵ j ll^s ij,^k 3 ^s V , ^{k 5}Л ,

В области гидрида (переменные обозначаем верхним индексом «1») 0 <  x <  h

где l_f – градиентный параметр в области гидрида.

В этом случае, напряжения T j и m i _jk выражаются как

(1) (1) f                            (1) f

^T 11 = ^T x = - = ^{( X} f ^{+ 2 ц} f ^{) s} x ^- K f ^s V , 58ц

^T 22

^ =

^T j ( ^ f ^s V ^- K f ^s V )⁵ j ^{+ 2} ^ f ^s j

^T 33

= <’ =

d w f ^ds 22 ^d w f ds ₃₃

= ^X f ^s V

= ^X f ^s V

—Kf ^s V ,

K f s V .

m ijk = ^lf { ( ^X f ^s V , k ^- K f ^s V , k ) ⁵ ij + ^{2 ц} f ^s ij , k } ,         ⁽⁸⁾

°(?

^T 11

— ITT m111.1

= T (1)

^T 11

I- ⁽¹⁾ = ¹ f 41,11

где K f = X f + у ц f - объемный модуль гидрида.

= ( X f + 2 ц f ) s«- 1 f

d2s(1) 3           , xf

. 2 I K f ^s V ,

Следующее упрощение для рассматриваемой задачи состоит в предположении постоянства распределения деформации фазового превращения по объему гидрида E V = const [22; 24]. С учетом этого окончательно получим

I

^f d x

^ =° 33 =X f ( s«

-

, 2 ' s f 5x2

Уравнение равновесия в области гидрида

Tij =(Xf sV  Kf sV )5j + 2цf sij mijk = lf (Xf sV,k5ij + 2цf sij,k ).

Se i¹)   H^’  _n

—— - 1 2-- x- = 0.

d x       d x ³

Интегрирование уравнений (11) и (13) дает выражения для деформаций и их производных

Ex (x ) = C1 + C2 ex / l + C3 e- x / l, ex1’ (x) = D1 + D2 ex/lf + D3 e-x/lf, de.   C ш C -X  ae»   D2 x/1,  D-

—x = — e ' ' - — e l , —— = — e ^f - — e ^f , (14)

5x     l l        dx    lf а также перемещений u (x) = C0 + C1 x + C2 lex / l - C3 le- x/ l,

u(1) (x ) = D0 + D1 x + D2 lfex /lf - D3 lfe - x /lf.(15)

Из уравнений (11) и (13) следует, что cx = (X + 2ц) Ci,    a = (X f + 2ц f) D1- Kf e V. (16)

Для определения восьми неизвестных постоянных C i , D i , i = 0,3 требуется сформулировать граничные условия, четыре из которых являются классическими u ⁽¹⁾ ( 0 ) = 0, u ( 1 ) = 0, u ⁽¹⁾ ( h ) = u ( h ) , а^ ( h ) = c x ( h ) , (17)

где h – толщина слоя гидрида.

Дополнительные граничные условия в рамках градиентной теории упругости ex1’ (0) = 0, ex (1) = 0, ex1’ (h) = 0, ex (h) = 0 . (18)

Таким образом, задача определения полей перемещений, деформаций и напряжений в слое сведена к решению восьми линейных уравнений (17), (18) относительно неизвестных постоянных C i ,D i , i = 0,3 .

Прокомментируем последние два условия в (18) на контактной границе между гидридом и матрицей при x = h . Обычно используемые в градиентной теории упругости дополнительные граничные условия на контакте двух разнородных пластин – это требования гладкости – непрерывности деформаций и их производных. Однако в нашей задаче о фазовом превращении такие требования приводят к некорректным результатам, а именно к смещению контактной границы в область гидрида u ( h ) < 0. Это физически невозможно, поскольку гидрид при образовании стремится расшириться, что приводит к u ( h ) >  0 . Для условий (18), принятых в статье, этот недостаток устраняется (рис. 3).

Энергетические соотношения для градиентной теории . Согласно [24], полная энергия системы «матрица – гидрид» записывается в виде

J = — fc„ e„ dV + — [c ^f e, f dV - p * u, dS - ij ij ij ij i i

2 _V            2 _{Vf            S}

• - K_f e V J u n dS -y vf V f + y S S f ^ min.

S f

Для рассматриваемого случая одноосной деформации слоя с учетом полученного решения

¹ J c, e „. dV = ¹ SC 1 ( X + 2ц ) х 2 V 2

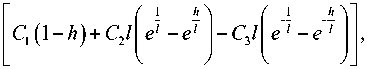
¹ J c f e j dV = ¹ SD 1 [ ( X f + 2 ц f ) D 1 - K f e V ] х

^{2 V} f           ²                                   (20)

х [ D 1 h + D ₂ l_f ( e h / l f - 1 ) - D ₃ l_f ( e ^- h / l f - 1 ) ] ,

[                    h - h

J p * u_i dS = 0, K_f e V J u n dS = K_f e ^f_VS C 0 + C 1 h + C ₂ le¹ - C 3 le l

S                         S f                     _

-YVf Vf + YSf Sf = -YVf hS + YSf S , где pi* – компоненты вектора поверхностных нагрузок; Vf , Sf — объем и поверхность гидрида; yVf , YSf — коэффициенты, учитывающие вклад физико-химических эффектов в полную энергию при фазовом превращении.

Результаты и их обсуждение

Особенности распределения перемещений и деформаций в слое, состоящем из гидрида и матрицы. Классическое распределение перемещений и деформаций по толщине слоя достигается при малых величинах градиентных параметров l,l_f . Чем больше эти параметры, тем значительнее отклонение от классического решения. На рис. 1 представлены распределения перемещений при l=l f = 0,01 (классический вариант).

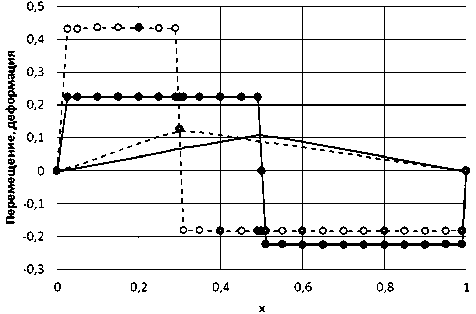
Рис. 1. Распределение перемещений (сплошная линия: h = 0,5; пунктирная линия: h = 0,3) и деформаций (черный круг: h = 0,5; серый круг: h = 0,3) по толщине слоя

Fig. 1. Distribution of displacements (solid line: h = 0.5; dotted line: h = 0.3) and deformations (black circle: h = 0.5; gray circle: h = 0.3) over the layer thickness

Таким образом, в классическом решении перемещения являются линейными функциями, а деформации – кусочно-постоянными функциями (кроме окрестности границ отрезка и контакта). При уменьшении толщины слоя гидрида h величина деформации увеличивается.

Как следует из (16), напряжения являются постоянными по толщине слоя, но величина их зависит как от линейного размера гидрида h , так и от значений градиентных параметров l,l_f .

На рис. 2 показаны зависимости напряжения, индуцированного появлением гидрида, от толщины слоя гидрида h при различных значениях градиентных параметров, принимаемых одинаковыми l=l_f . Белый маркер соответствует l=l f = 0,01; светло-серый – 0,1; темно-серый – 0,2; черный – 0,5.

Из рисунка следует, что увеличение h ведет к росту (по абсолютной величине) сжимающих напряжений. Причем при размерах гидрида в диапазоне 0,2–0,3 классическое решение дает более чем в 1,5–2 раза выше уровень напряжений, чем решение в рамках градиентной теории упругости. Однако при достижении значений h > 0,5 различия между двумя вариантами решения нивелируются.

Если учесть, что градиентный параметр l=l_f соизмерим с линейным размером объекта (в нашем случае – зерна), этот результат можно трактовать как наложение полей напряжений от соседних зерен. То есть по сути это есть определенная граница, переход за которую уравнивает значимость результатов расчета по двум принципиально различным подходам.

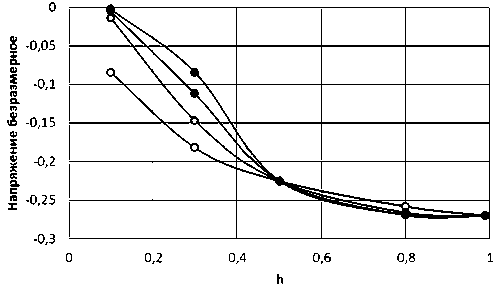
Рис. 2. Зависимости напряжения от толщины слоя гидрида ( h )

Fig. 2. Stress dependences on hydride layer thickness ( h )

Как уже отмечалось выше, поля перемещений и деформаций при больших градиентных параметрах максимально отличаются от классического решения. На рис. 3 показаны распределения перемещений и деформаций (аналогично рис. 1) для l = l f =1.

Линиями показаны перемещения (сплошная – h = 0,5; пунктирная – h = 0,3; точечная – h = 0,1), а маркерами (и линиями) деформации (черный круг – h = 0,5; серый круг – h = 0,3; белый круг – h = 0,1). Отличия от классического решения (см. рис. 1) состоят в «сглаживании» деформаций и отклонении их от кусочно-постоянной функции, значительном уменьшении уровня максимальных деформаций – более чем на порядок.

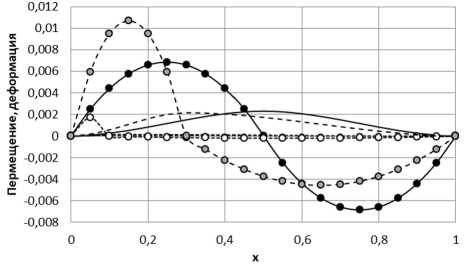
Рис. 3. Распределение перемещений (линии) и деформаций (маркеры с линиями) по толщине слоя

Fig. 3. Distribution of displacements (lines) and deformations (markers with lines) over the layer thickness

Особенности влияния различных факторов на полную энергию системы. Зависимости J = f(h) , где J – полная энергия системы, показаны на рис. 4: пунктирная линия – l = l f = 1,0; белый круг – l = l f = 0,5; светло-серый круг – l = l f = 0,3; темно-серый круг – l = l f = 0,2; черный круг – l = l f = 0,1; сплошная линия – l = l f = 0,01 (классическое решение). Значения параметров, характеризующих физико-химические процессы γ Vf = 0,3; γ Sf = 1.

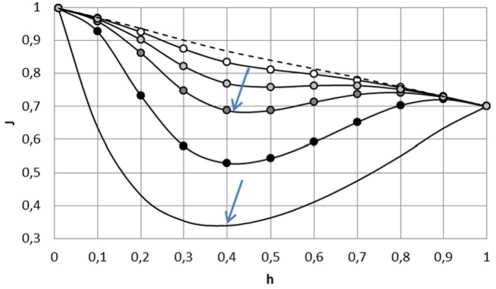
Рис. 4. Зависимость полной энергии от толщины слоя гидрида (γ Vf = 0,3; γ Sf = 1)

Fig. 4. Dependence of total energy on hydride layer thickness (γ Vf = 0,3; γ Sf = 1)

Очевидно, что классическое решение дает более глубокий минимум, достигаемый при h * = 0,4. Решение в рамках градиентной теории упругости дает более «мелкий» минимум, несколько смещаемый в сторону увеличения h *. При увеличении градиентного параметра локальный минимум «выполаживается», переходя в глобальный минимум при h* → 1.

Обращает на себя внимание установленная закономерность, а именно наличие «глобального минимума». Здесь опять следует напомнить, что параметр l = lf соизмерим с линейной величиной зерна. Полученный результат в целом позволяет предположить, что энергетический выигрыш системы в пределах одного зерна меняется нелинейно, и, проходя через минимум, далее выигрыш энергии снижается по мере увеличения линейной величины зерна, то есть по мере увеличения влияния соседних объектов – зерен. Переход частных минимумов в общий глобальный минимум энергии можно связать со сменой контролирующего фазовое превращение механизма, когда превращение охватывает значительный объем материала и его микроструктурные особенности теряют свою значимость. При этом, однако, сохраняется влияние выигрыша полной энергии в процессе фазового превращения, как это уже было показано ранее [23; 24].

В качестве экспериментального аналога этого заключения можно рассмотреть механизм диффузии водорода в материалах (в частности, в магнии), основанный преимущественно на теории диффузии [33–36]. Принято считать, что диффузия по границам зерен вносит определяющий вклад в температурном интервале до 0,6 T пл ( T пл – температура плавления) и в поликристаллических материалах в общем случае осуществляется в несколько этапов, или, как принято говорить, реализуется в виде ряда сменяющих друг друга диффузионных режимов [37]. Диффузия водорода в магний имеет свои особенности. Ввиду малого размера экранизированного протона, одновременно с движением по границам зерен водород абсорбируется и в приповерхностном слое металла. Далее происходит проникновение вещества в объем. Через определенное время диффузионные фронты, возникшие в результате его протекания через соседние границы зерен и поверхность, практически полностью перекрываются, и концентрация выравнивается по всему диффузионному фронту. Это представление необходимо дополнить существенным замечанием: в тех локальных микрообъемах, где концентрация водорода оказывается достаточной для образования гидрида, происходит фазовое превращение и возникают напряжения, которые нарушают идеальную картину диффузии и влияют на дальнейшее образование MgH 2 . При всех несомненных достоинствах диффузионных моделей проникновения водорода в металл они не учитывают вероятность одновременно происходящего гидридного превращения. В контексте данной работы необходимо заметить, что, согласно существующей точке зрения [38], гидридные зародыши магния при соприкосновении образуют сплошной слой, препятствующий дальнейшему проникновению водорода вследствие малого коэффициента диффузии водорода в гидриде, однако роль образования напряжений/деформаций на границе раздела «гидрид – матрица» в процессе фазового перехода не учитывается. Полученные результаты позволяют восполнить этот пробел и сместить акцент именно на роль напряжений на границе раздела «гидрид – матрица» в процессе фазового перехода. Для понимания этого обратимся вновь к однопараметрической градиентной теории.

Максимально простой вариант этой теории (Айфан-тис) в одномерном варианте для декартовой системы координат можно записать как:

, Зе а, = E ех + 1E—-, xx дx

где E – модуль упругости; l – градиентный параметр, имеющий размерность длины.

Если в некотором диапазоне x0 < x < x1 напряжение постоянно о x =C, то соотношение (21) представляет собой дифференциальное уравнение относительно εx , решение которого имеет вид еx = - - Ciexp(--),(22)

El где C1 – постоянная интегрирования.

Пусть при x = x 0 , s _x =s _x 0 , тогда

E x = — -(— -E x o)exP( xVx).

EE l

Распределение деформации при заданных парамет-

C рах x = 0; x = 2; ε = 0,001; = 0,01 для различных 0          1         x0

значений градиентного параметра l показаны на рис. 5.

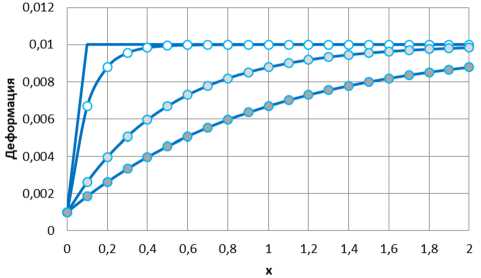
Рис. 5. Распределение деформации для различных значений градиентного параметра: l = 0,01 – линия; l = 0,1 – белый маркер; l = 0,5 – светло-серый маркер; l = 1,0 – темно-серый маркер

Fig. 5. Strain distribution for different values of the gradient parameter: l = 0.01 – line; l = 0.1 – white marker; l = 0.5 – light gray marker; l = 1.0 – dark gray marker

C σ

Здесь параметр = играет роль классической де-EE формации, соответствующей приложенному напряжению, а параметр εx0 – деформация, задаваемая на границе участка. При малом значении l = 0,01 деформация практически сразу (скачком в классической теории) выходит на уровень E = 0,01. С ростом градиентного параметра

(с отклонением от классического решения) выход на уро- вень E = 0,01 достигается при больших значениях x.

С позиции гидридного превращения из этого следует главный вывод: распределение деформации (напряжений) вблизи зародыша гидрида носит не локальный, а дальнодействующий характер. Результаты, представленные на рис. 5, позволяют утверждать, что локальное образование гидрида энергетически выгодно только при определенном объеме гидрида. По мере увеличения его объема энергетический выигрыш исчерпывается, и система «гидрид – матрица» переходит в новое энергетическое состояние.

Таким образом, градиентная теория хорошо согласуется с представлениями о механизме образования гидрида магния, объясняя возникновение «переходных» зон (областей с небольшим процентным содержанием гидрида) и влияния напряжений на разных этапах его образования.

Заключение

Согласно литературе, применение градиентной теории упругости оправданно на микроуровне: в масштабах расчетной области, сравнимых с размером (или менее) зерна. Таким образом, при больших размерах области матрицы и зародыша гидрида по сравнению с некоторым характерным размером, например, размером зерна, мы должны ориентироваться на классическое решение. При малых размерах зародыша гидрида, сравнимых или меньших (и/или значительно меньших) размера зерна,