Анализ уравнений гидравлического расчета газопровода при развитом режиме течения

Для гидравлического расчета магистральных газопроводов разными авторами [1-13] предложены различные формулы, которые получены на основе приведенных выше уравнений при изотермическом режиме движения газа по линейным участкам:

dP   dy  Xw ²     d w²

--+ g — +--+ a --= 0    m - pdx   dx  2 D    dx 2           ⁽¹⁾

_ M = pwS , P = ZpRT

Здесь в развитом турбулентном режиме течения X = 0,11 ( k ID ) ^0,25; a - постоянные и ( a = 1,1 ).

Значение плотности, определенное из уравнения состояния реального газа (из третьего уравнения системы), вставляется в первое и второе уравнения (1.10). Из вновь полученного второго уравнения определяется значение скорости и вставляется во вновь полученное первое уравнение. Таким образом, получается обыкновенное дифференциальное уравнение [14].

dP ( P ² - A ) + GP ³ + Л P = 0 ,  (2)

dx где , aZRTM2, r g dy; д _ XZRTM2 -

A = G =

S ²         ZRT dx        2 DS ²

постоянные.

Переписав уравнение (2) в разделенном по переменным виде, получим

P ² - A GP³ +N P

dP = dx .

Интегрируем левую сторону по P , а правую сторону по x . Для интегрирования левой стороны используем метод неизвестных коэффициентов и получим ре- шение

AG, P AG + A, GP ² +Л

----In---In----:----- = X ’

Л   P_o    2 G Л    GP₀ ² +Л

где P - значение давления на входе в рассчитываемый участок.

Подобное, но относительно w ² , решение системы (2) приведено в [3]. Общим недостатком обоих решений является то, что она не позволяют получить явную зависимость давления от координаты x в целом виде (кроме отдельных случаев нулевых значений коэффициентов) и проследить за изменением давления в зависимости от каждого коэффициента из списка A, G и Л .

Вернемся к уравнению (3) и интегрируем его численным методом.

Интегрирование проведем по методу трапеций с постоянным шагом A P по формуле

^P

Axi = x - xi-1 = —(f + f-1), где

A — Р . p

Gp ³+ Л р'

После того как вычислено значение A x

, вычислялись значения отдельных членов уравнения движения из (1).

Вычислительные эксперименты проводились при следующих данных: Р₀ = 5,6 • 10⁶, 4,0 • 10⁶,2,0 • 10⁶ Па , dy / dx = 0; 0,1; - 0,01; и    при    постоянных     D = 1,02 м ,

ZRT = 150000м2/c2,  w0 = 10м/c  и % = 0,018 до достижения p = 1,0 • 106 Па. Результаты вы- числительных экспериментов и их анализ при различных условиях функционирования магистрального газопровода подробно изложены в работах [11, 14].

Изменения давления и среднерасходной скорости в горизонтальном газопроводе типичные, которые приведены в учебниках. Вниз по потоку становятся более ин- тенсивными увеличение скорости и уменьшение давления. При положитель- ном уклоне трассы часть энергии теряется на подъем газа, в связи с чем давление падает быстрее; и наоборот, при спуске трассы благодаря силе тяжести уменьшается перепад давления.

Характер изменения абсолютного зна- чения первого члена уравнения движения аналогичен характеру изменения среднерасходной скорости. В зависимости от значения параметра dy / dx распределение энергии перестраивается.

Для случая dy / dx = 0,1 на начальном участке доля силы тяжести больше на 4% чем доля силы сопротивления. Увеличение абсолютной величины члена

1 dP р dx

вниз

по потоку обусловлено увеличением среднерасходной скорости w . Доля силы тяжести снижается от 52% в начале до 4% на расстоянии 54 км, хотя значение слагаемого pdy / dx остается постоянным вниз по течению. Удивительно также, что доля d w2

слагаемого a--растет вниз по тече- dx 2

нию. Но несмотря на увеличение средне расходной скорости более чем в 5,6 раза доля этого слагаемого не превышает 3-4% от энергии перепада давления.

При dy / dx = - 0,01 на начальном участке 12% энергии, затраченной на преодоление силы сопротивления, компенсируется силой тяжести. В дальнейшем этот показатель уменьшается до 2% при достижении давлением значения 10 6 Па .

В этом случае также доля изменения скорости растет вниз по потоку, но не превышает 2,5% от энергии, затраченной на потери напора.

Расчеты велись, как уже заметили, до достижения давлением значения 10⁶ Па . Соответствующие этому расстояния составляли при dy / dx = 0,1 - 54 км, при dy / dx = 0 -82 км, а при dy / dx = - 0,01 -87 км.

Попытка определить постоянное значение dy / dx , при котором обеспечивается течение с постоянной скоростью газа без участия нагнетателя, не увенчалась успехом.

Разработанная программа была также использована при изучении закономерностей потока и доли слагающих уравнения движения при постоянном линейном (массовом) отборе газа из МГ. При этом в уравнениях и обозначениях (кроме решения (4)) следует принять

M ( x ) = M _o — mx = M _o ( 1 — P x ) .

Здесь Mo - значение массового расхода в начале участка; m, в - действительная ( -1  -1- кг м с ) и приведенная ( м ) относительно M интенсивность линейного отбора газа. Это значит, что если длина участка составляет в-, то рассматривается тупиковый участок, а если она меньше чем в 1, то транзитный расход газа через участок составляет M = M„ - mx.

i 0

В случае путевого отбора коэффициенты A и Л, использованные в уравнении (4), становятся переменными. Расчеты показали, что при dy / dx = 0 и в = 1/20000м 1 имеет место практически линейное падение среднерасходной скорости. Интенсивность падения давления на тупиковом участке меньше, чем в случае постоянного расхода. То есть с уменьшением массы переносимой среды сила сопротивления падает (до нуля), притом кривая более полога в конце участка. Доля изменения скорости не превышает 1%. Изменения основных показателей потока и слагающих уравнения движения при dy/ dx = -0,01 и в = 1/20000м-1 приведены на рис 1.1.-1.3.

В отличие от кривых скорости для горизонтальных МГ, в обсуждаемом случае среднерасходная скорость сначала (до 10км) растет (до 2%) и далее убывает. Сила сопротивления и доля первого члена монотонно падают, а доля силы тяжести растет. Кривая давления в этом случае вогнутая, в то время как в обычных расчетах (при dy / dx = 0 и в = 0 м-1) она выпуклая.

Общей чертой численных результатов, полученных для тупиковых МГ, является немонотонное изменение результатов в конечной части пути. Причиной тому является неучет изменения режима течения и температуры газа. Известно, что при изменении среднерасходной скорости значение коэффициента сопротивления, в целом, становится переменным, а при замет- ном изменении температуры следует учитывать эффект Джоуля-Томсона.

Таким образом, изучение факторов уравнения движения сжимаемой среды в газопроводах при развитом турбулентном режиме обтекания шероховатости показало, что:

• -    при отсутствии путевого отбора и малых значениях параметра dy / dx основная энергия нагнетателей тратится на преодоление силы трения, которая растет вниз по течению;

• -    несмотря на постоянное значение pdy / dx в случаях постоянного расхода доля силы тяжести убывает вниз по потоку, а при путевом отборе доля силы тяжести растет;

• -    вниз по течению доля изменения скорости в энергетическом балансе растет и в рамках проведенных расчетов не превышает 3-4%, что является основанием для пренебрежения этим фактором при проведении гидравлических расчетов (при постоянном расходе по пути из решения (4) следуют известные для расчета магистральных газопроводов формулы [3, 10];

• -    при путевом отборе газа из МГ среднерасходная скорость и давление вниз по потоку уменьшаются: при большем отборе падение их значений более интенсивно;

• -    кривая давления при путевом отборе может иметь вогнутую форму.

  Изменения факторов по длине газопровода при Sina^J.I

  

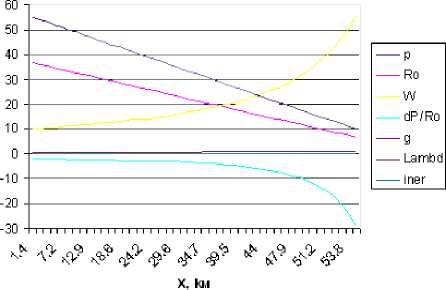
  Рис 1.1.

  
  

Изменения факторов по длине газопровода при sina=0

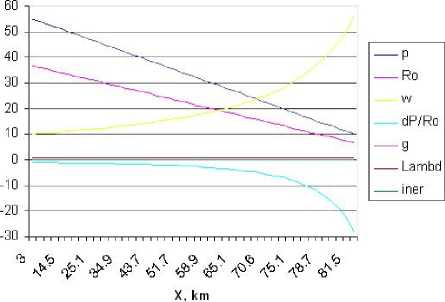
Рис 1.2.

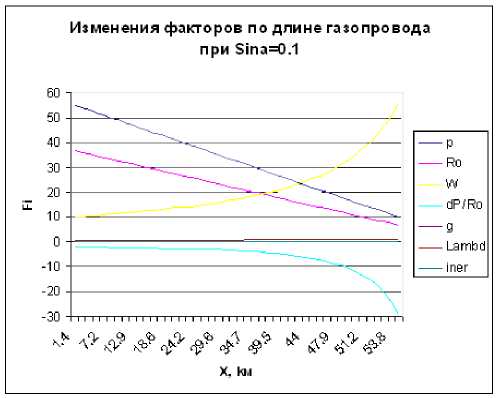
Рис 1.3.