Анализ условий, влияющих на свойства конструируемых признаков 3D-изображений

В современных условиях во многих областях науки, техники и промышленности возникла большая потребность в системах распознавания реальных трехмерных (далее 3D) объектов. Сюда можно отнести робототехнику, результаты которой широко используются, например, в военном деле, в промышленности, в космонавтике и т.д. [1 –3].

В индустриально развитых странах ведутся интенсивные исследования по решению проблем распознавания пространственных объектов на основе их изображений. Однако в этой области возникают большие сложности и нерешенные задачи, связанные:

• •    с созданием математических методов описания изображений реальных объектов;

• •    разработкой алгоритмов формирования инвариантных к пространственному положению и масштабу объекта наборы признаков, использование которых обеспечивает высокую надежность распознавания данных реальных 3D-объектов;

• •    другими задачами теоретического и прикладного характера.

Несмотря на возрастающую потребность в развитии методов машинного зрения, их эффективность при распознавании 3D-изображений значительно уступает возможностям человека. Например, в работе [4] рассматривается необходимость формирования моделей с обзором 360 ° , что человеку не требуется. В работах [5, 6] рассматриваются новые подходы к анализу формы, чтобы приблизить машинное понимание объекта к человеческому. Поэтому разработка нового метода анализа и распознавания 3D-изображений является актуальной и перспективной задачей.

В статье рассматривается новый подход к анализу и распознаванию 3D-изображений, основанный на методах и положениях стохастической геометрии и представляющий собой развитие идей из [1]. В работе [14] представлены практические эксперименты по примене- нию разрабатываемого метода. Целью данной статьи является дальнейшее развитие нового метода распознавания 3D-объектов, направленное на анализ условий, формирующих свойства признаков. Теоретические исследования в данном направлении будут способствовать повышению качества конструируемых распознающих систем за счет сознательного выбора процедур, позволяющих извлекать признаки с заданными свойствами. Ниже кратко представлена математическая модель предлагаемого метода – гипертрейс-преобразование [7].

1.    Математическая модель гипертрейс-преобразования

Обозначим через B ( n , r ) плоскость на расстоянии r от начала координат и вектором нормали П = [sin ф- cos to , sin ф- sin to , cos ф ], где и - угол между осью 0 х и проекцией вектора η на плоскость 0 xy , φ – угол между вектором η и осью 0 z .

Исходная 3D-модель изображения F сканируется сеткой параллельных плоскостей B ( n(to, ф) , r ) под различными углами обзора ω и φ согласно узлам опорной сетки на сфере [7]. Идея построения опорной сетки заключается в следующем. Каждой сканирующей сетке параллельных плоскостей с парой углов (ω, φ) на единичной сфере сопоставим точку, которая будет являться точкой касания со сферой плоскости, параллельной плоскостям данной сетки. Множество точек на сфере образует сетку, которая называется опорной (рис. 1). Чтобы конструируемые признаки обладали свойством инвариантности к пространственному повороту 3D-изображения, опорная сетка должна иметь равномерное распределение точек на сфере.

Результат пересечения каждой сканирующей плоскости B ( n(to, ф) , r ) с трёхмерной моделью F характеризуется числом, получаемым с помощью функционала Hyper T: G = Hyper T ( F П B ( n(to, ф) , r )).

Результаты сканирования удобно занести в гипер-трейс-матрицу (будем называть её гипертрейс матри- ца 3TM), у которой ось 0ω направлена горизонтально, ось 0φ – вертикально, ось 0r – вглубь [8].

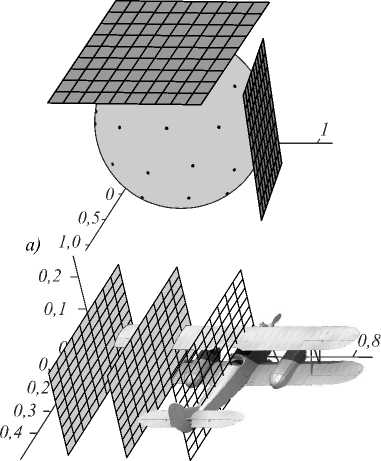
Рис. 1. Построение опорной сетки на сфере (а); процесс сканирования 3D-изображения сеткой параллельных плоскостей (б)

Далее обрабатываются столбцы и строки сформированной матрицы с помощью функционалов Hyper Θ, Hyper Ω и Hyper P . В результате вычислений получается значение признака Res ( F ) исходной 3D-модели изображения в виде композиции четырех функционалов [8, 9]:

R es ( F ) = Hyper 0 ° Hyper Q ° Hyper P ° Hyper T ( F sect ) . Приставка Hyper для обозначения функционалов используется авторами для подчеркивания, что речь идет об обработке 3D-объекта.

Изображение фигуры сечения F sect сканируется решеткой параллельных прямых l (ρ, θ) с дискретным шагом Δρ между линиями под различными углами θ до завершения полного обхода в 2π радиан. Результаты сканирования аналогичным образом формируются в двумерную трейс-матрицу, у которой ось 0ρ направлена вертикально, а ось 0θ – горизонтально [10].

Признак 2D-изображения получается сворачиванием строк и столбцов трейс-матрицы и имеет структуру в виде композиции трех функционалов [1, 10]:

П ( F s_ect ) = Hyper T ( F sect ) = © ° P ° T ( F sect П l ( 6 , p ) ) .

Объединяя полученные формулы, окончательно получаем следующую аналитическую структуру гипертриплетного признака 3D-изображения:

R es ( F ) = Hyper 0 ° Hyper Q ° Hyper P °

° Hyper T ( 0 ° P ° T ( F sect П l ( 6 , p ) ) ) .

2.    Особенности формирования гипертрейс-матрицы

Если результаты сканирования 3D-изображения (признаки сечений) заносить в матрицу от точки (0, 0,1) оси 0z в направлении по часовой стрелке от оси 0x, то при формировании гипертрейс-матрицы 3ТМ [7, 9] возникают определенные трудности сохранения целостности ее структуры – нарушается порядок следования строк и столбцов друг за другом в матрице. Это вызвано тем, что равномерная сетка на сфере неизоморфна равномерной сетке на плоскости.

При повороте 3D-изображения глубинные строки сохраняют порядок следования элементов, так как при повороте не изменяется порядок следования сечений (дискретная форма пространственного объекта). Однако при повороте 3D-изображения порядок следования элементов в горизонтальных строках (ось 0ω) и вертикальных столбцах (ось 0φ) матрицы 3ТМ в общем случае без наложения дополнительных условий не сохраняется из-за произвольной пространственной ориентации 3D-изображения.

Так, при обработке функционалами трехмерная матрица сворачивается в число в строго заданных направлениях (сначала глубинные, далее вертикальные, а затем горизонтальные строки). Поэтому из-за произвольной ориентации тела в пространстве возможен случайный поворот матрицы относительно оси 0 r в пространстве 0ωφ r . Произвольное нарушение порядка следования строк матрицы друг за другом в данных фиксированных направлениях приведёт к изменению значения вычисляемого признака и, как следствие, инвариантность распознавания 3D-изображения будет нарушена.

В связи с этим правила нумерации узлов опорной сетки, по которым формируется трехмерная гипер-трейс-матрица и определяется порядок следования ее элементов, должны определятся не относительно координатных осей, а относительно произвольно ориентированного пространственного объекта.

Для определения направления нумерации узлов опорной сетки достаточно идентифицировать некоторые опорные ключевые точки – узлы опорной сетки, которые однозначно определяются вне зависимости от пространственной ориентации 3D-объекта. Данные опорные точки определяют начало отсчёта (первую глубинную строку), от которого начинает заполняться гипертрейс-матрица. Например, построение гипер-трейс-матрицы при нумерации узлов опорной сетки от первой ключевой точки по часовой стрелке в направлении второй ключевой точки для заполнения элементов матрицы.

Ключевые точки характеризуют уникальные свойства пространственного объекта, на основании которых могут быть построены гипертриплетные признаки, инвариантные к повороту 3D-изображения. Так, в качестве ключевой точки можно взять узел на опорной сетке, который соответствует сетке секущих плоскостей, содержащей максимальное по площади сечение исходного пространственного объекта.

Стоит отметить, что при повороте объекта секущие плоскости (например, сечения, перпендикулярные главной оси объекта) будут соответствовать другим точкам опорной сетки по сравнению с точками сетки до его поворота. Поэтому необходимо задавать правило инвари- антной нумерации узлов опорной сетки, которое позволяет получать однородную структуру матрицы, при обработке функционалами строк и столбов которой получаются одинаковые значения признака вне зависимости от пространственной ориентации 3D-объекта.

Порядок следования горизонтальных строк (ось 0и) и вертикальных столбцов (ось 0ф) при произвольной пространственной ориентации трехмерного тела имеет некоторые особенности в зависимости от метода построения гипертрейс-матрицы 3ТМ . Приведем один из примеров нумерации узлов опорной сетки (методов построения гипертрейс-матрицы).

Из всего множества возможных узлов опорной сетки выбирается ключевая точка, имеющая отличительное значение по какому-либо признаку. Данная ключевая точка считается за северный полюс, от которого по сфере начинают строиться меридианы. Данные меридианы разбивают сферу на двуугольники с вершинами в северном и диаметрально противоположном ему относительно центра сферы южном полюсе. Нулевым меридианом будет считаться тот, который проходит через точку S с координатами (1; 0; 0). В случае совпадения указанной точки S с одним из полюсов сферы - через точку (0; 1; 0).

Нумерация в каждом двуугольнике идет от северного полюса к южному по часовой стрелке. Обход всех двуугольников совершается по часовой стрелке (если смотреть на северный полюс сверху), начиная и заканчивая двуугольниками, чьи стороны содержат нулевой меридиан.

В этом случае смысл строк и столбцов гипертрейс-матрицы 3TM останется тем же с той лишь разницей, что тройке (и i , ф j , r k ) соответствует элемент матрицы со значением П( F sect ) и номером (5 t , у s , r k ), соответствующая точка которого лежит в пределах от долготы 5 1 до 5 t+i , в полосе широт от у s до у s+i . Соответственно, все точки, принадлежащие одному двуугольнику, соответствуют всем значениям одного вертикального столбца матрицы 3TM .

Горизонтальные строки определяют порядок считывания граней выпуклого многогранника (в частности, икосаэдра). Так как нулевой меридиан определяется на основе глобальной системы координат, от которой зависит ориентация 3D-объекта, то вертикальные столбцы (ось 05) представляют собой дискретный аналог периодической кривой.

• 3.    Анализ свойств гипертрейс-матриц для построения инвариантного класса признаков 3D-изображений

Трейс-матрицы 3ТМ и ТМ являются удобным инструментом для анализа движения распознаваемых объектов и их масштабных изменений [1, 10]. Гипер-трейс-матрица 3ТМ - 3D-трейс-образ исходного пространственного изображения, который содержит информацию о первоначальном объекте. Аналогично, трейс-матрица ТМ - 2D-трейс-образ плоского изображения 2D-фигуры сечения, полученного при пересечении плоскости B ( п(®, ф) , r ) исходного 3D-объекта F .

В зависимости от вида преобразования, применяемого к 3D- и 2D-изображению, свойства гипертрейс-и трейс-матриц будут различными. Поэтому целесообразно рассмотреть данные матрицы отдельно.

Свойства трейс-матриц в зависимости от операций, применяемых к 2D-изображению сечения [1, 10]:

• 1)    Поворот 2D-изображения в плоскости сечения.

В локальных осях плоскости сечения каждая сканирующая прямая 1 будет характеризоваться расстоянием р от локального начала координат до нее и углом 9 ее направляющего вектора и локальной оси абсцисс (0 <  9 < 2 п ):

1 ( ° , Р ) = { ( x , У ) : x cos 0 + y sin 0 = р } .

Если прямую в плоскости сечения повернуть на угол п радиан, то она будет параллельна сама себе, при этом ее направляющий вектор и вектор нормали, лежащие в плоскости сечения, будут направлены в прямо противоположную сторону: 1 ( 0 , р )= 1 ( 0 + п , р ) для любого значения угла 9. Так как вектор нормали прямой в плоскости сечения определяет направление порядка следования пересечений 2D-изображения сеткой сканирующих прямых (элементы матрицы ТМ по вертикальной оси 0р), то через каждый интервал длины п по оси 09 переворачиваются столбцы трейс-матрицы (ось 0р).

Если прямую в плоскости сечения повернуть на угол 2п радиан, то она совпадёт сама с собой, в том числе ее направляющий вектор и вектор нормали: 1 ( 0 , р ) = 1 ( 0 +2 л , р ). Поэтому матрица ТМ будет 2п-периодична в направлении горизонтальной оси 09.

В связи с этим, если первоначальное 2D-изобра-жение поворачивается на угол в, то происходит сдвиг столбцов трейс-матрицы ТМ в горизонтальном направлении на в единиц, так как сканирующей прямой 1 ( 0 , р ) исходного изображения F sect будет соответствовать сканирующая прямая 1' ( 0 + в , р ) повернутого изображения F ‘ sect : 1 ( 0 , р ) = 1' ( 0 + в , р ). Поэтому 2D-трейс-образ изображения будет сдвигаться вперёд или назад на |в| единиц по горизонтальной оси 09 в зависимости от знака угла в. При этом порядок следования столбцов друг за другом не изменится, так как порядок сканирований сетками прямых формируется последовательно друг за другом (по возрастанию значений угла 9 от 0 до 2п радиан).

• 2)    Перенос 2D-изображения в плоскости сечения.

Если происходит сдвиг исходного 2D-изображения на некоторый вектор { a - cos в ; a - sin в } длины a под углом в к локальной оси абсцисс, то точка ( x ‘, y ‘) сдвинутого изображения F ' будет соответствовать точке ( x , y ) исходного изображения F следующим образом: x ‘ = a - cos в , y ‘ = a - sin р .

Поэтому сканирующей прямой 1 ( 0 , р ) исходного изображения F sect будет соответствовать сканирующая прямая 1 ‘ ( 0 ‘, р ‘) сдвинутого изображения F ‘ sect :

x ' cos 0' + y ' sin 0' = р' ,

(x + a cos в) cos 0’ + (y + a sin в) sin 0' = р', x cos 0'+ y sin 0' + ( a cos в cos 0'+ a sin в sin 0') = р', x cos 0'+ y sin 0' = р- a cos (0'-в).

Так как сканирующей прямой 1 ( 6 , р ) исходного изображения F sect соответствует сканирующая прямая 1 ( 6 , р - a - cos ( 6 - в )) сдвинутого изображения F ' sect , то при переносе исходного 2D-изображения на некоторый вектор { a - cos в ; a - sin в } произойдет сдвиг строк трейс-матрицы ТМ в вертикальном направлении на a - cos ( 6 - b ) единиц вверх или вниз в зависимости от знака выражения. При этом вертикальные столбцы матрицы ТМ остаются на своём месте и не сдвигаются вдоль оси 09, так как при сдвиге 2D-изображения угол сканирующей прямой 1 ( 6 ‘, р ‘), соответствующий сканирующей прямой l ( 6 , р ) исходного изображения, не изменяется: 6 ’= 6 .

Таким образом, при сдвиге 2D-изображения в плоскости сечения в трейс-матрице ТМ увеличивается или уменьшается количество нулевых элементов в вертикальных столбцах (ось 0р) в зависимости от его приближения или удаления от локального начала координат. Поэтому 2D-трейс-образ изображения будет растягиваться вдоль оси 0р на соответствующее число, определяемое вектором переноса.

• 3)    Масштабирование 2D-изображения в плоскости сечения.

Если происходит масштабирование исходного 2D-изображения в р раз, то точка ( x ‘, у ‘) масштабированного изображения F ‘ sect будет соответствовать точке ( x , y ) исходного изображения F sect следующим образом: x ‘ = р- x , у ‘ = р- у .

Поэтому сканирующей прямой l ( 6 , р ) исходного изображения F sect будет соответствовать сканирующая прямая 1 ‘ ( 6 ‘, р ‘) масштабированного изображения F ‘ sect :

x ' cos 6’ + у ' sin 6’ = р', x cos 6' + у sin 6' = (р'/р), p ^ 0.

Таким образом, при р ‘ = р-р и 6 ’= 6 сканирующая прямая 1 ‘ ( 6 ‘, р ‘) совпадет с прямой 1 ( 6 , р ). При масштабировании в р раз 2D-изображение сечения будет пересекать больше (при р >1) или меньше (при р < 1) сканирующих прямых, так как изменяются размеры 2D-изображения при сохранении значения шага сканирования. В связи с этим, в вертикальных строках столбцах трейс-матрицы ТМ соответственно изменится количество ненулевых элементов, которые обозначают свойства пересечений плоского изображения сеткой прямых. Следовательно, 2D-трейс-образ изображения будет расширяться или сужаться в р раз вдоль оси 0р.

Стоит отметить, что при масштабировании изображения будут изменяться еще и значения элементов трейс-матрицы ТМ . Так, если в качестве функционала Т взять длину отрезка пересечения сканирующей прямой 2D-изображения сечения F sect , то значения элементов трейс-матрицы для сканирующих прямых 1 ( 6 , р ) и 1 ‘ ( 6 ‘, р ‘) будут равны соответственно:

Т ( F sect П 1 ( 6 , р ) ) = ( x 2 - x ) ² + ( у 2 - у 1 ) ² = 1 о ,

Т ( F sect П 1 '(6' , р’ ) ) = V( x 2 - x ’ ) ² + ( у 2 - у ’ ) ² =

= V (р-x 2 -р-x ) +(р-у 2 -р-у1 ) = р- 10.

Следовательно, значение элементов трейс-матрицы ТМ при р > 1 увеличатся в р раз, а при р < 1 -уменьшатся в р раз, если в качестве значения трейс-функционала была взята длина высекаемого отрезка. В зависимости от вида функционала Т значения элементов матрицы могут изменяться по-разному.

Свойства гипертрейс-матриц в зависимости от операций, применяемых к 3D-изображению:

• 1)    Поворот 3D-изображения в пространстве.

В глобальных осях 3D-объекта каждая сканирующая плоскость B будет характеризоваться расстоянием r от начала координат до нее и углами и и ф (0 <  и < 2 п ,0 <  ф <  п ), где n = [cos и-sin ф , sin и- sin ф , cos ф ] - единичный вектор в R 3 , и - угол между осью 0 x и проекцией на плоскость 0 xy прямой b с B , ф - угол между осью 0 z и прямой b :

B ( п ( и , ф ), r ) = { ( x , у , z ) : x - cos и- sin ф +

+ у - sin и - sin ф + z - cos ф = r }.

Как уже было сказано выше, для учета произвольной неизвестной пространственной ориентации объекта необходимо определить ключевые точки, которые однозначно идентифицируются для исходного F и повернутого F' изображений еще до занесения результатов сканирования в гипертрейс-матрицу, так как данные точки характеризуют уникальные свойства 3D-объекта, не зависящие от его вращения в пространстве. Ключевым точкам будут соответствовать плоскости B ( n(8, y) , r ) и B' ( n(8 ' , Y) , r ), для которых B ( n(8,y) , r )= B ( n(8 ^Y) , r ).

Если сканирующую плоскость B в пространстве повернуть относительно прямой d, проходящей через фиксированный северный полюс сферы (первая ключевая точка), на угол п радиан, то она будет парал-—— лельна сама себе и ее вектор нормали n будет направлен в прямо противоположную сторону, так как для любого значения угла 8 имеются равенства

B ( n(8, Y) , r )= B ' ( п(8+п, п - y) , r ) и n = -n' :

П ( 8 + п , п-y ) = [cos ( 8 + п ) - sin ( п-y ) , sin ( 8 + п ) - sin ( п-y ) ,cos ( п-y ) ] = = [ - cos 8- sin y , - sin 8 - sin y , - cos y ] = -n ( 8 , y ).

Другими словами, плоскостям B ( n(8,y) , r ) и B ' ( п(8+п, п - y) , r ) будут соответствовать диаметрально противоположные точки опорной сетки на сфере. Так как вектор нормали плоскости определяет направление порядка следования сечений 3D-объекта сеткой сканирующих плоскостей (элементы матрицы 3ТМ по глубинной оси 0 r ), то через каждый интервал длины п по оси 08 переворачиваются вертикальные столбцы (ось 0 y ) и глубинные строки (ось 0 r ) гипертрейс-матрицы 3ТМ .

Если плоскость B повернуть в пространстве относительно прямой d на угол 2п радиан, то она совпадёт — сама с собой, в том числе и ее вектор нормали n :

B ( η(δ, γ) , r )= B′ ( η(δ+2π, γ) , r ) и ^→η =-η^→′ для любого значения угла δ. Поэтому матрица 3ТМ будет 2π-периодична в направлении горизонтальной оси 0δ.

• 2)    Перенос 3D-изображения в пространстве.

Если происходит сдвиг исходного 3D-изображения на некоторый вектор

{a⋅cosλ⋅sinβ;a⋅sinλ⋅sinβ;a⋅cosβ} длины a, то точка (x′, y′, z′) сдвинутого изображения F будет соответствовать точке (x, y,z) исходного изображения F следующим образом:

• x ′ = x + a ⋅ cos λ ⋅ sin β ,

• y ′= y + a ⋅ sin λ⋅ sin β , z ′ = z + a ⋅ cos β .

Поэтому сканирующей плоскости B ( η(δ, γ) , r ) исходного изображения F будет соответствовать сканирующая плоскость B′ ( η(δ ′ , γ ′ ) , r′ ) сдвинутого изображения F :

• x ′⋅ cos δ′⋅ sin γ′ + y ′⋅ sin δ′⋅ sin γ′ + z ′⋅ cos γ′ = r ′ ,

( x + a ⋅ cos λ⋅ sin β ) ⋅ cos δ′⋅ sin γ′+

+ ( y + a ⋅ sin λ⋅ sin β ) ⋅ sin δ′⋅ sin γ′+ + ( z + a ⋅ cos β ) ⋅ cos γ′= r ′ , x ⋅ cos δ′⋅ sin γ′+ y ⋅ sin δ′⋅ sin γ′+ z ⋅ cos γ′ = = r ′- a ⋅ (cos λ⋅ sin β⋅ cos δ′⋅ sin γ′ +

+ sin λ⋅ sin β⋅ sin δ′⋅ sin γ′+ cos β⋅ cos γ′ ), x ⋅ cos δ′⋅ sin γ′ + y ⋅ sin δ′⋅ sin γ′+ z ⋅ cos γ′ =

= r ′- a ⋅ ( sin β⋅ sin γ′⋅ cos ( δ′-λ ) + cos β⋅ cos γ′ ) .

Так как сканирующей плоскости B ( η(δ, γ) , r ) исходного изображения F соответствует плоскость

B ′ ( η ( δ , γ ), r ′ -

• - a ⋅ ( sin β⋅ sin γ⋅ cos ( δ-λ ) + cos β⋅ cos γ ) )

сдвинутого изображения F , то при переносе исходного трехмерного изображения на некоторый вектор { a ⋅ cos λ⋅ sin β ; a ⋅ sin λ⋅ sin β ; a ⋅ cos β } произойдет сдвиг строк гипертрейс-матрицы 3ТМ в глубинном направлении на a ⋅ sin β⋅ sin γ⋅ cos( δ – λ ) +cos β⋅ cos γ ) единиц вверх или вниз в зависимости от знака выражения. При этом вертикальные столбцы и горизонтальные строки матрицы 3ТМ остаются на своём месте и не сдвигаются вдоль осей 0ω и 0φ, так как при сдвиге 3D-изображения угол сканирующей плоскости B′ ( η(δ ′ , γ ′ ) , r′ ), соответствующей сканирующей плоскости B ( η(δ, γ) , r ) исходного изображения, не изменяется: δ ′ = δ , γ ′ = γ .

Таким образом, при сдвиге 3D-изображения в ги-пертрейс-матрице 3 ТМ увеличивается или уменьшается количество нулевых элементов в глубинных строках (ось 0 r ) в зависимости от его приближения или удаления от глобального начала координат. Поэтому 3D-трейс-образ изображения будет растягиваться вдоль оси 0 r на соответствующее число, определяемое вектором переноса.

• 3)    Операция масштабирования 3D-изображения в пространстве.

Если происходит масштабирование исходного 3D-изображения в µ раз, то точка ( x ′, y ′, z′) масштабированного изображения F будет соответствовать точке ( x , y ,z) исходного изображения F следующим образом: x ′ = µ⋅ x , y ′ = µ⋅ y , z ′ = µ⋅ z .

Поэтому сканирующей плоскости B ( η(δ, γ) , r ) исходного изображения F будет соответствовать следующая сканирующая плоскость B′ ( η(δ ′ , γ ′ ) , r′ ) масштабированного изображения F :

x′⋅cosδ′⋅ sinγ′ + y′⋅ sinδ′ ⋅ sinγ′ + z′⋅cosγ′ = r′, µ⋅ x⋅ cosδ′⋅sinγ′+µ⋅ y ⋅ sinδ′ ⋅ sinγ′ + +µ⋅z⋅cosγ′ = r′, x ⋅ cos δ′⋅ sin γ′+ y ⋅ sin δ′⋅ sin γ′+ z ⋅ cosγ′ = r ′/µ,

µ ≠ 0.

Таким образом, при r ′ = µ⋅ r и δ ′ = δ , γ ′ = γ сканирующая плоскость B′ ( η(δ, γ) , r′ ) совпадет с плоскостью B ( η(δ, γ) , r ). При масштабировании в µ раз 3D-изображение будет пересекать больше (при µ > 1) или меньше (при µ < 1) сканирующих плоскостей, так как изменяются размеры 3D-изображения при сохранении значения шага сканирования. В связи с этим в глубинных строках гипертрейс-матрицы 3 ТМ соответственно изменится количество ненулевых элементов, которые обозначают свойства сечений пространственного изображения сеткой плоскостей. Поэтому 3D-трейс-образ изображения будет расширяться или сужаться в µ раз вдоль оси 0 r .

Стоит отметить, что при масштабировании изображения будут изменяться значения элементов гипер-трейс-матрицы 3ТМ . Рассмотрим, как изменятся значения элементов гипертрейс-матрицы, если в качестве функционала Hyper Т взять вычисление площади сечения.

Так как изначально задан полигональный 3D-объект, то любое из его сечений плоскостью можно представить совокупностью многоугольников произвольной формы. Так как любой многоугольник можно разбить на множество треугольников, то площадь сечения F sect исходного изображения F будет равна:

^Π( F sect )⁼ ∑ S ∆ .

Площадь сечения F′ sect масштабированного изображения F будет равна:

Π ( F s ′ ect ) = ∑ S ∆ ′=µ ² ⋅ ∑ S ∆ =µ ² ⋅Π ( F sect ) .

Таким образом значения элементов гипертрейс-матрицы 3 ТМ при µ > 1 увеличатся в µ ² раз, а при µ < 1 – уменьшатся в µ ² раз, если в качестве признака сечения была взята площадь. В зависимости от вида трейс функционала Hyper Т значения элементов матрицы могут изменяться по-разному.

Таким образом, зная заранее, как реагирует 3D-трейс-образ исходного пространственного объекта на то или иное его движение и масштабирование, можно изначально конструировать признаки с заранее заданными свойствами. В частности, возможно построение классов признаков, сенситивных и/или инвариантных к тем или иным преобразованиям 3D-изображения.

Заключение

Актуальность создания нового метода анализа и распознавания 3D-объектов связана с разработкой такого метода сканирования, который обладал бы одновременно и универсальностью, и быстродействием. Заметим, что разрабатываемый метод является развитием подходов, используемых для анализа 2D-изображений [1]. Возможности повышения быстродействия разрабатываемого метода при сканировании 3D-объектов рассмотрено в [11].

Гипертрейс-преобразование позволяет создавать инвариантное описание пространственного объекта вне зависимости от его пространственной ориентации, положения и масштаба.

Трейс-матрицы 3ТМ и ТМ являются удобным инструментом для анализа движения распознаваемых объектов и их масштабных изменений. Гипертрейс-матрица – 3D-трейс-модель исходного пространственного изображения, которая содержит всю информацию о первоначальном объекте. Возможности извлечения различных свойств 3D-объекта описаны в [12, 13].

Применяя при обработке матрицы соответствующие функционалы, которые инвариантны к приведенным выше преобразованиям изображения и изменениям строк гипертрейс- и трейс-матриц, мы будем конструировать признаки, инвариантные к группе движений и масштабированию 3D-изображения. Строгое математическое описание данных свойств (изменений матрицы в результате движения 3D-изображения) содержится выше в данной статье.

Работа выполнена при поддержке гранта РФФИ (проект №15-07-04484).