Анализ устойчивости эффективного алгоритма линейной локальной фильтрации сигналов

Линейная локальная фильтрация (ЛЛФ) - основной этап любой системы обработки цифровых сигналов и анализа изображений. Процед уры ЛЛФ используются как на этапе предварительной обработки для восстановления и улучшения качества сигналов, так и на этапе высокоуровневой обработки - для построения описания анализируемых объектов и сцен. Одной из центральных проблем, возникающих при реализации процед ур ЛЛФ, является проблема вычислительной сложности и времени обработки. В авторских работах [1,2] предложен алгебраический подход к построению нового класса вычислительно эффективных алгоритмов ЛЛФ - эффективных алгоритмов , которые конструируются как композиции известных алгоритмов ЛЛФ. Цель настоящей работы - анализ устойчивости эффективных алгоритмов с точки зрения реализуемой ими линейной системы с постоянными параметрами (ЛПП системы).

Работа организована следующим образом.

В первом разделе дается очень краткое изложение результатов работ [1,2], в которых был введен класс эффективных алгоритмов. Эти же работы рекомендуются читателю в случ ае возникновения неясностей в указанном разделе.

Во втором разделе представлен ряд хорошо известных положений теории цифровой обработки сигналов, связанных с вопросами устойчивости и физической реализуемости ЛПП систем. Этот раздел является вспомогательным и приведен исключительно из соображений цельности послед ующего изложения.

Третий и четвертый разделы являются центральными в работе. В третьем разделе представлен анализ устойчивости эффективных алгоритмов, выполненный стандартными средствами, представленными во втором разделе.

В четвертом разделе исследование устойчивости эффективных алгоритмов выполнено на основе анализа максимальной погрешности выходного сигнала. Преимущество этого подхода перед традиционно используемым состоит в возможности анализа поведения ЛПП системы обработки для случая конечного выходного сигнала, мощность которого оказывается заведомо ограниченной. Такой подход оказывается целесообразным именно для эффективных алгоритмов, ориентированных на обработку именно конечных сигналов.

В заключении работы приводятся благодарности фондам, поддерживающим данную работу, и список литературы.

Эффективный алгоритм над множеством алгоритмов ЛЛФ

Настоящий раздел содержит краткое изложение необходимых сведений по эффективным алгоритмам ЛЛФ из работ [1,2]. Для упрощения изложение ведется в терминах одномерных сигналов.

Рассмотрим задачу ЛЛФ Z , заключающуюся в вычислении одномерной линейной свертки конечного входного сигнала { x ( n )} „ '=0 длины N с конечной импульсной характеристики (КИХ) { h ( m jj^ J :

M - 1

y (n ) = h (n) * x (n )= ^h (m)x (n - m )

m = 0                          (1)

n = M - 1, N - 1, результатом решения которой является получение сигнала { y ( n )} N = o ^{M + 1} длины N - M , называемого выходным сигналом . В общем случае отсчеты всех сигналов являются элементами некоторого коммутативного кольца K с единицей .

Для решения задачи (1) существ ует целый ряд известных алгоритмов ЛЛФ, которые условно мож- но разбить на множества [3-7]: алгоритмы прямой свертки ADC , алгоритмы быстрой свертки AFC и рекурсивные алгоритмы ARF . Идея, предложенная в работах автора [1,2], заключается в использовании некоторого опорного множества алгоритмов ЛЛФ A c A DC U A FC U A RF (представленных на практи- ке в виде программ) и априорной информации о за-

= ( { h ( m Ж 3 , )

даче ЛЛФ 3 0

, которая известна до

момента ее решения и представлена в виде КИХ {h (m)}M=0 и априорной информации 3x о свойствах обрабатываемого сигнала, для получения алгоритма, удовлетворяющего требованию эффективности. Требование эффективности подразумев ает, что искомый алгоритм в вычислительном плане:

• -    для любой задачи ЛЛФ Z оказывается не хуже

наилучшего алгоритма опорного множества ( свойство эффективности алгоритма),

• -    для некоторых задач ЛЛФ Z оказывается лучше наилучшего алгоритма опорного множества ( свойство строгой эффективности алгоритма).

Таким образом, определение способа построения эффективного алгоритма заключается в конструировании отображения

( 3 q , A ) м A ³ , (2) которое для конкретного опорного множества алгоритмов A и заданной априорной информации 3 ₀ дает алгоритм A ³ с наименьшей вычислительной сложностью решения соответствующей задачи (1).

След ует отметить, что идея использования множества алгоритмов для построения «наилучшего» в некотором смысле алгоритма была предложена в 70х годах академиком Ю.И.Журавлевым [8] для построения корректного алгоритма распознавания. Работы [1,2] автора настоящей работы развивают эту идею применительно к задаче ЛЛФ, используя другое формализованное представление алгоритма и, как следствие, иную алгебраическую систему.

Для конструирования отображения (2) в работах [1,2] вводится алгебраическая система алгоритмов ЛЛФ: конкретизируются отношения между алгоритмами (лучше, хуже и т.п.), а также операции (распространения, сужения и сложения). Далее, вводится операция расширения опорного множества алгоритмов A , построенная на основе простого эквивалентного преобразования выражения (1). Результатом применения этой операции к опорному множеству A алгоритмов ЛЛФ оказывается его расширение [ a ] . При этом алгоритмы из расширения [ а ] удовлетворят определенной модели алгоритма, названной в указанных работах моделью CR . Ниже приведено описание этой модели алгоритма ЛЛФ.

Модель CR алгоритма

Шаг 1 – Предварительная обработка:

K x -1                       ________

~ ( n ) = E g x ( k ) x ( n — k ) , n = 0, N — 1.           (3)

k = 0

Шаг 2. Вычисление сверток по всем интервалам допустимого покрытия { D s } ^ - 0 :

~ s ⁽ n ⁾⁼ E ~ s ^{( m} ) ~ ⁽ n ^{- m} )

me Ds(4)

( n = 0, N - 1, s = 0, S - 1 ).

Шаг 3. Объединение результатов (4):

S - 1

~(n )= E ~s(n).

s = 0

Шаг 4 – Окончательная обработка:

Kh + Kx - 2

y(n)=   E~(t)y(n - t)+~(n) n=0, N - 1.

t = 1

Модель CR алгоритма - Конец

В представленном описании модели:

• -    { g x ( k )} K = о * — КИХ предварительной обработки входного сигнала;

• ^-    ~ ⁽ m ) = h ⁽ m ) * g h ⁽ m ) , где ^{ g h ⁽ к ^)} K = 01 - КИХ предварительной обработки импульсной характеристики исходного фильтра;

• ^-    ~ ⁽ m ) = g x ^{( m} ) * g h ^{( m} ) ;

• -    { h s ( m ) } ^S = 0 - покрытие для КИХ { h ( m ) } , удовлетворяющее ограничению:

S - 1

~ ( m ) = E h s ( m ) , s = 0

V s ^ j supp h_s ( m ) A supp h j ( m ) = 0 .

Тройка параметров ( K _h , K _x , S ) определяет порядок модели, множество алгоритмов модели CR одного порядка далее обозначается [ a ] c _r ( K h _{K S} ) . При этом искомое расширение первоначального множества алгоритмов вводится в виде:

^{[ A ]}=     ^{U [ A ]} CR ( K h , K x , s ) .

K h = 1, M - 1 K x = 1, N - 1 S = 1,2,...

Каждый алгоритм A CR e [ а ] из расширения (модели CR) на первом и втором шаге для вычисления соответствующих сверток (3) и (4) использует некоторые алгоритмы опорного множества A . В результате задача конструирования отображения (2) заключается в поиске в расширении [ а ] алгоритма с наименьшей сложностью. Такой алгоритм и определяется как алгоритм A ³ , индуцированный априорной информацией о задаче . Существенно, что индуцированный алгоритм A ³ e [ а ] оказывается эффективным над опорным множеством A , а при н екото-рых условиях - строго эффективным.

В общем случае, то есть при произвольном опорном множестве алгоритмов ЛЛФ, процесс построения эффективного индуцированного алгоритма оказывается чрезвычайно сложным. Однако для практики основной интерес представляет множество алгоритмов вида A _DC ∪ A _FC ∪ A _RF . В работах [1,2] показано, что для построения эффективного алгоритма над множеством A _DC ∪ A _FC ∪ A _RF достаточно построить индуцированный алгоритм над множеством алгоритмов A _DC ∪ A _FC . Алгоритмы множества A _DC ∪ A _FC относятся к алгоритмам постоянной сложности ( АПС ), у которых функция аналитической вычислительной сложности представима в виде выражения u _A ( M , N ) от параметров M и N задачи ЛЛФ. Там же показано, что процесс построения состоит из трех хорошо формализованных операций. Он представляет собой конечную (по объему вычислений) численную процедуру, которая дает решение в виде точных значений параметров модели CR (числовых и алгоритмических) для индуцированного алгоритма A ³ .

Основные положения теории цифровой обработки сигналов

Настоящий раздел содержит только хорошо известные положения т еории цифровой обработки сигналов, касающиеся вопросов устойчивости ЛПП систем. Он приведен исключительно из соображений цельности изложения. Более полная информация доступна в известных изданиях [3-7].

Как известно, прямое Z -преобразование X ( z ) последовательности { x ( n )} определяется формулой:

м

X ( z ) = 2 x ( n ) z - ⁿ .                              (7)

n = 0

Функцию X ( z ) называют Z -образом последовательности { x ( n )} . Справедливо предложение.

Предложение 1 (теорема о свертке) [5-7]. Пусть ^{ x ⁽ n ^)}{1 ⁽ n ^)} { y ⁽ n ^)} - некоторые последовательности,       связанные соотношением

y ( n ) = x ( n ) * h ( n ) тогда их Z -образы связаны соотношением Y ( z ) = X ( z ) • H ( z ) .

Передаточной функцией ( ПФ ) линейной системы с постоянными параметрами называется отношение Z-преобразований выходного и входного сигналов:

K = GF ( P ) .                                  (8)

Вид передаточной функции определяет, является ли конкретный линейный цифровой фильтр рекурсивным или нерекурсивным след ующим образом:

• -    рекурсивный цифровой фильтр - это цифровой фильтр с передаточной функцией вида (8), не содержащей общих множителей в числителе и знаменателе и имеющей ненулевые коэффициенты в знаменат еле;

• -    нерекурсивный цифровой фильтр - это цифровой фильтр, передаточная функция которого принимает вид полинома по степеням z ^- 1 после сокращения всех общих сомножителей в выражении (8):

M - 1

H ( z ) = ^ h ( m ) z — m .

m = 0

Легко показать, что КИХ-фильтры, реализуемые с использованием алгоритмов прямой свертки, являются нерекурсивными .

Рассмотрим далее практически важный случай, когда сигналы являются вещественными, то есть когда вместо кольца K отсчеты сигналов принадлежат более «богатой» алгебраической структуре - полю R . Очевидно, что числитель и знаменатель ПФ общего вида (8) являются полиномами переменной z ^{- 1}. Поэтому они могут быть факторизованы следующим образом:

П ( 1 - q i z ^- )

H(z’■ B n          •                      ,9)

где B – некоторая постоянная величина. Величины { q i } в выражении (9) ПФ называются нулями ПФ , а { p j } - полюсами ПФ ( B e R , q i е С , p j е С ). В работе использованы след ующие определения для устойчивой и реализуемой ЛПП системы:

• -    ЛПП система называется устойчивой , если при любой ограниченной входной последовательности выходная последовательность также ограничена;

• -    ЛПП система с импульсной характеристикой { h ( m )} называется физически реализуемой , если V m <  0 h ( m ) = 0.

Справедливы след ующие предложения.

Предложение 2 [4]. Необходимым и достаточным условием устойчивости ЛПП системы является выполнение соотношения: ^| h ( m ) < ^ .

m

Предложение 3 [3]. Физически реализуемая ЛПП система является устойчивой тогда и только тогда, когда все полюса ее ПФ находятся внутри единичного круга Z-плоскости: V j |p₇ -| < 1 .

Из этих двух предложений след ует очевидное.

Следствие 1. Любой нерекурсивный цифровой фильтр является устойчив ым.

Устойчивость эффективного алгоритма ЛЛФ

Примем далее след ующие обозначения:

• - X ( z ) , Y ( Z ) - Z-преобразования для входной и выходной последовательностей,

  -    H ( z ) - ПФ для КИХ-фильтра { h ( m )} “ _{= 0}* ,

  -    G x ( z ) , G _h ( z ) - ПФ для КИХ-фильтров

{ g h ( k^ ( g h ( 0 ) = 1 ) и { g x ( k ) K 0¹ ( g x ( 0 ) = 1 ) .

Легко показать справедливость утверждений.

Предложение 4. Пусть A - опорное множество алгоритмов постоянной сложности. Любой алгоритм A^CR модели CR с допустимым набором числовых параметров реализует физически реализуемую ЛПП систему.

Лемма 1. Пусть A - опорное множество алгоритмов постоянной сложности, A ³( Z ) - индуцированный алгоритм задачи Z. Если A ⁽ Z ) е ^{[ а} ] _сд ( 1,_{1 5} ) , тогда A ³( Z ) реализует устойчивую ЛПП систему.

Следствие 2 (леммы 1). Пусть A - опорное множество алгоритмов постоянной сложности, и пусть индуцированный алгоритм A ³( Z ) задачи Z не является строго эффективным. Тогда A ³( Z ) реализует устойчивую ЛПП систему.

Более общая ситуация рассматривается в лемме.

Лемма 2. Пусть входной сигнал и КИХ фильтра являются конечными последовательностями над полем R , и A - опорное множество алгоритмов постоянной сложности. Индуцированный алгоритм A ³( Z ) задачи Z реализует устойчивую ЛПП систему тогда и только тогда, когда нули передаточных функций    КИХ-фильтров

G x ( z ) , G h ( z ) расположены внутри единичной окружности Z-плоскости.

Доказательство:

Ситуация K _h = 1, K x = 1 .

В этой ситуации лемма (ее достаточное условие) является следствием леммы 1, поскольку в этом случае ПФ G x ( z ) = G _h ( z ) = 1 и индуцированный алгоритм реализует нерекурсивный линейный цифровой фильтр. Поскольку в этой ситуации обратное условие ни при каких обстоятельствах не может быть выполнено, справедливо и необходимое условие.

Ситуация ( K h >  1 ) v ( K x = 1 ) .

Выражение для схемы вычисления в алгоритме модели CR [1,2] может быть переписано с помощью Z-преобразования следующим образом:

Y (Z )Gx (z )Gh (z )= (X (z )Gx (z))(H (z Gx (z)).    (10)

В выражении (10) правая часть характеризует Z-преобразование последовательности { ~ ( n )} , которая используется в выражении (6) алгоритма модели CR для вычисления окончательного результата свертки:

K h + K x - 2

y ⁽ n ) = Е ~ ⁽ t ) y ⁽ n ^- t ⁾⁺ ~ ⁽ n ) .

t = 1

Заметим, что последовательность { y ( n )} получается из последовательности { x ( n )} посредством применения нерекурсивных алгоритмов из опорного множества A . В силу следствия 1, эти алгоритмы реализуют устойчивую ЛПП систему и, следовательно, последовательность { y ( n )} является ограниченной. Поэтому свойства индуцированного алгоритма A ³( Z ) полностью характеризуются свойствами преобразования (11).

Заметим также, что поскольку вычисления в поле вещественных чисел R на ПЭВМ производятся не абсолютно точно, значения последовательности { y ( n )} и, соответственно, ее Z -преобразование получаются с некоторой погрешностью:

~(Z) = (H (z )Gh (z))(X (z )Gx (z ))+ e(z), (12)

что не позволяет сократить общие множители в правой и левой части выражения (10).

ПФ для цифрового фильтра, реализующего обработку (11), имеет вид:

YZ=___ 1__

~(z) Gx (z )Gh (z) G(z).

Тогда для устойчивости физически реализуемой ЛПП системы, реализуемой индуцированным алгоритмом A ³( Z ) в соответствии с предложением 4, необходимо и достаточно выполнения условия предложения 3, то есть нахождения внутри единичного круга Z-плоскости полюсов ПФ G ( z ) , при этом полюса G ( z ) совпадают с нулями ПФ G x ( z ) , G _h ( z ) .

■

Лемма 3. Пусть входной сигнал и КИХ фильтра являются конечными последовательностями над полем GF ( p ) и A - опорное множество АПС. Тогда индуцированный алгоритм A ³( Z ) задачи

Z реализует устойчивую ЛПП систему.

Доказательство:

Ситуация Kh = 1, Kx = 1 рассматривается аналогично лемме 2. В ситуации (Kh > 1)v (Kx = 1) выра- жение для схемы вычисления алгоритма модели CR может быть переписано с помощью Z-преобразования след ующим образом:

Y (Z )Gx (z )Gh (z ) == ( X (z )Gx (z))(H (z )Gx (z)> ~(Z),      (14)

где ~(Z) - есть Z-преобразование последовательности {y(n)}, которая используется в выражении (6) алгоритма модели CR (см. также выражение (11)). Вычисления в конечном поле GF (p) на ПЭВМ производятся абсолютно точно, поскольку это операции с целыми числами по модулю некоторого простого числа. Поэтому значения последовательности {~(n)} и, соответственно, ее Z-преобразования получаются абсолютно точно. Тогда выражение (14) может быть преобразовано к виду:

Y (Z ) = X (z) H (z) ^ Y (Z)(X (z ))-1 = H (z). (15)

Получ енное выражение по казывает, что ПФ индуцированного алгоритма, испо льзуемого для вычисления свертки в простом поле Галуа GF ( p ) , в точности совпадает с ПФ для КИХ { h ( m )j mf =- ₎ ¹ . Такая ПФ, в силу конечности исход ной импульсной характеристики, соотв етствует усто йчиво й ЛПП системе.

■

На практике для современных ПЭВМ и конечных длин N обрабатываемых сигналов требование устойчиво сти для ЛПП системы оказыв ается чрезмерно сильным. Это объясняется тем, что погрешности пред став ления данных и выполняемых операций чрезвычайно малы и при сравнительно малых конечных длинах слабо влияют на результат . Однако при больших длинах обраб атыв аемых сигналов (обычно более нескольких тысяч отсчетов в зависимости от вида ПФ) такое влияние оказыв ает-ся уже существ енным. В след ующем разделе представ лен подход, которы й позволяет производить более скрупулезный анализ «устойчивости» ЛПП системы, реализуемой алгоритмом модели CR, в плане вносимых погрешностей в результат обработки. Этот подход без изменений мо жет быть использован для аналогичного анализа рекурсивных фильтров.

Анализ погрешности выходного сигнала для эффективного индуцированного алгоритма ЛЛФ

Рассмотрим ситуацию , когд а входной сигнал и КИХ ф ильтр являются конечными последователь -ностями над по лем R (поскольку случ ай сигналов над GF ( p ) оказывается тривиальным). В соответствии с леммо й 2 существуют параметры КИХ предварительной обработки { g_h ( k )} K = 0¹ , при которых ЛПП система, реализуемая индуцированным алгоритмом, не явля ется устойч ивой. Однако на-пря мую использовать вывод ы об устойчивости или неустойчивости ЛПП системы, ко торую реализует соотв етствующий эфф ективный алгоритм, не совсем ко рректно . Действительно , в соотв етст-вии с постанов кой зад ачи вычисления св ертки и моделью алгоритма CR, выходной сигнал { y ( n )} N o1 является конечным (по длине) и, как следствие, в сегд а ограниченным. Следов ательно , факт неустойчивости реализуемо й алго ритмо м ЛПП системы еще не означ ает невозможность его использования для решения конкретной задач и ЛЛФ ко неч ного сиг нала.

Для более точного определения границ области применимости конкретного алгоритма модели CR след ует оценить некоторым образом погрешность, которая вносится в результат вычислений – отсчеты выходного сигнала. Для этого рассмотрим отдельно последний этап алгоритма модели CR, который отвечает за обработку с использованием рекурсивного уравнения (11). В качестве величины погрешности, которая характеризует рассогласование истинного и получаемого выходных сигналов, используем максимальную ошибку рассогласования.

ПФ для цифрового фильтра, реализующего обработку (11), как было показано ранее, имеет вид:

YZ)     =___1___

~ ( z ) G'   G x ( zG ( z ) '

Представим G ( ) в виде

G ( z ) =

K h + K x - 2/        A

П ( 1 - q k z ^{- 1} ) k = 1

K h + K x - 2      1

п = k=1   (1 - qkz )

K h + K x - 2 П G k ( z ) . k = 1

Тогда вычисления в (11) можно произвести последовательно фильтрами G k ( z ) с ПФ вида:

G k ^{( z} ) = / ¹ a , ^{( 1 -} q k ^z )

k = 1, K _h + K x

- 2.

Для каждой такой ПФ соответствующее рекуррентное уравнение обработки имеет вид:

y_k ⁽ n ) = q k y k ⁽ n ^{- 1 )+} y_k - 1 ⁽ n ) , n = 0? N -" ,   k = 1, K_h + K x - 2;

где

У о ^{( n ) =} ~ ^{( n} ) , У ^{( n} N y K_h + K x - 2 ^{( n} ) , ⁿ = ⁰ N ^- 1.

Рекуррентно е уравнение (16) справ едливо толь ко в аналитич еско м смысле. При реализации этих рекурсивных вычислений на ПЭВМ в отсчеты y _k ( n ) ( k = 0, K _h + K x - 2 ) вносится погрешность, связанная как с ограниченным формато м хранения веществ енных чисел, так и с пог решно -стя ми выполнения операций их умножения и сло -жения. Таким об разом, наблюд аемо е при об работке одного k -го сигнала в n -ой позиции значение имеет вид , указанный в выражении (17), при-вед енном ниже. Здесь:

- £ _k ( n ) - (общая) погрешность операций умножения, сложения и представления в ПЭВМ значения, которое получено на k -ом шаге в n -ой позиции, то есть y _k ( n ) -го;

- £ _к ( n ) - накопленная в значении y _k ( n ) погрешность, которая включает в себя интегрально все предшествующие погрешности, связанные с получением этого значения, начиная с самого первого шага алгоритма.

Ук (n ) + e y (n ) =

У ( n ) + e ₀ ( n ) ,        n > 0, к = 0,

У к - 1 ( 0 ) + e к - 1 ( 0 ) , n = 0, к = 1, K h + K x - 2, (17) q k • ( Ук ( ^{n -} 1 )^+e к ( ^{n -} 1 ) )

+ (Ук-1 (n)+eк-1 (n))+eк (n), n > 0, к = 1, Kh + Kx - 2.

Отсюда получаем след ующее двумерное рекуррентное соотношение для ошибок вычисления в (16):

max|e^ (n) = max|q1e1 (n -1)+ e^(n)+ e1(n) = max( q^ |eУ (n -1) + 2^ )=q^ max^(n -1))+ 2^.

Полученное неоднородное линейное рекуррентное соотношение относительно функции max| e y ( n )

имеет решение в виде: max e y ( n ) =

= q j n maxlk ⁽ 0 ^{))+ 2 e} max 'q ¹, ^{1 (} Ч 1| Ф- 1 ) 9 1| ^{- 1}

Учитывая начальные условия из (18) для вели чины e^7(0), имеем окончательно:

e ₀ ( n ) ,      n >  0, к = 0,

e £ ( n ) = ^e У - 1 ( 0 ) ,   n = 0, к = 1, K _h + K _x - 2,

^max| ^{e У ( n} 1 ^e max

L r₊2 q 1 n - 11 I q ^{1 + 2} UTT =

V                 у

Ч к ' ^e к ^{( n - 1 ) + e} к - 1 ^{( n ) + e} к ^{( n} ) ,

n >  0, к = 1, K _h + K _x - 2.

₌       I q \n ^{+1 +}| q \n ^{- 2}

= ^e ma^x      q 1| - 1

(q\\^1)-

Полученное рекуррентное соотношение не позволяет получить аналитическое решение для e к ( n ) в явном виде. Однако оно дает возможность получить верхнюю границу для e к ( n ) в простых частных случаях, на основании которой можно дать рекомендации по использованию алгоритма модели CR для практически важных ситуаций.

Пусть далее e max - это максимальная погрешность ошибки e _к ( n ) для конкретных ПЭВМ, операционной системы и среды программирования. Примеры погрешностей представления вещественных чисел на IBM PC c операционной системой Windows и средой программирования Builder C++ приведены в таблице 1. Тогда можно получить оценки e к ( n ) в след ующих случаях.

Таблица 1 - Точность машинного представления числа «1/3» в С/С++

тип C/С++	пример представления	количество верных разрядов
		деся-тич-ных	двои чных
float	0.3333333432674407959	7	23
double	0.3333333333333333148	16	53
long double	0.3333333333333333334	18	60

Учитывая также тот очевидный факт, что ошибка вычислений при росте номера k функции не уменьшается, то есть

Vк > 1 max e к (n) > max e к_1 (n), на основании полученных соотношений можно сформулировать след ующее предложение.

Предложение 5. Для рекуррентного уравнения обработки (16) с параметрами |q _k | ^ 1 ( к >  1 ) максимальная погрешность результата удовлетворяет неравенству:

I У( 1 >         l ^q 1|      ⁺ l ^q 1| ^{- 2}

max eк (n ) > emax    II'---- q1-1

.

Полученная формулировка, пригодная для любых | q _k | ^ 1, может быть использована для указания необходимых условий применимости алгоритма модели CR для обработки сигналов конкретных длин. А именно: необходимо, чтобы длина обрабатываемой последовательности удовлетворяла условию:

n* . | ^q 1 n ^{+ 1}^ ^q 1 n 2k2 <  ^А

| q1| - 1         emax где А - заданная максимальная погрешность результата.

В частности, при | q _k | = 2, имеем

Случай 1. q _k ^ 1, к = 0,1 .

Если k =0, тогда очевидно:

|^e 0 ⁽ n ⁾⁼l^e 0 ⁽ n ! <  ^e max      ⁽ n >  ^{0 )} .

Если k =1, тогда на основании (18) имеем:

*

n <  log 2

[

3 V

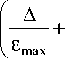
ЛА ² ) у)

= log z l----- ^{+ 2} I ^- log 2 ^{( 3 )} .

V max )

А при А =1 приблизительное максимальное значение

*

n величины n имеет вид: max

*

п _ max

= log 2

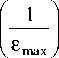
- 1 = r 2 - 1

где r2 – указанное в таблице 1 количество верных двоичных разрядов в представлении вещественного числа. В частности, при представлении вещественных чисел в формате float , допустимая максимальная длинна обрабатываемого сигнала не может быть больше величины n max = 22. Очевидно, что практический интерес такие длины не представляют.

Случай 2. q k = 1 .

Случай q k = 1 имеет большое практическое значение, поскольку он соответствует выбору представления КИХ в виде многочлена (полинома или полиномиального сплайна в ситуации, когда первоначальное представление получено для непрерывной КИХ). Для случаев к = 0, к = 1 имеем:

|Ey (n )=|E0 (n) 0) , max|Ey (n) = max|Ey (n -1)+ E0 (n) + E1(n) = = max(Ey (n - 1))+ 2Emax = (2n + 1)Emax •

Для к = 2 имеем:

max E 2 ( n ) = max E 2 ( n - 1 ) +E y ( n ) + E 2 ( n ) =

= max^ ( n ^- 1 ) ) + max j e f ( n ) ) + E m_ax =

= ^{max (} £ 2’ ⁽ n ^- 1 ^{))+ 2 (} n + 1 ^)E max .

Полученное неоднородное линейное рекуррентное соотношение относительно функции max| E y ( n )

имеет решение в виде:

^max| ^{E y ( n} ) = ^{max (E} 2 ^{( 0 ))+ E} max ^{n ( n + 3 )} = = ^E max ^{( n} 2 ^{+ 3 n +} 1 )

Для к = 3 получаем:

max E y ( n ) = max E y ( n - 1 ) + E 2 ( n ) + E ₃ ( n ) =

= ^{max (E} y ⁽ n ^- 1 ^{))+ max (E} 2 ⁽ n ^{))+ E} max =

= max ( E ^y ( n - 1 ) ) + E _max ( n ² + 3 n + 2 ) .

Решая это неоднородное линейное рекуррентное соотношение относительно maxe3'(n), имеем:

max E.3' ( n

= ^ma x ^(E y ^{( o ))} + ^E max fу^{( n 2} + ^{1 1 ) + 2} n n

I n _ 2 11 , = E_m „„I--+ 2 n + — n + 1

max I 3           3

Учитывая практическую важность кубических сплайнов, последнее соотношение оформим в виде предложения.

Предложение 6. Для рекуррентного уравнения обработки (16) с параметрами |q _k | = 1 ( k = 0,3 ) максимальная погрешность выходного сигнала задается выражением (23).

Вводя обозначение для многочлена порядка K над Q в виде

K

P k ⁽ m ⁾⁼ E ^ j m , fe j ^{g q )} , j = 0

можно показать, что для произвольного k имеет место след ующее предложени е.

Предложение 7. Для рекуррентного уравнения обработки (16) с параметрами |qk| = 1 (k > 0) максимальная погрешность выходного сигнала удовлетворяет соотношению max|Ek (n )=EmaxPk (n ) .                          (24)

На основании полученных соотношений можно указать границы применимости алгоритма модели CR для случая КИХ, заданной в виде полинома или полиномиального сплайна K -ого порядка. А именно: в общем случае для рекуррентного уравнения обработки (16) с параметрами | q_k | = 1 ( k = 1, K ) максимальная погрешность результата не превышает заданную максимальную погрешность А , если максимальная длина обрабатываемого сигнала не превышает величины

n *„v =         max n .                 (25)

max

I            I      \ А )| ne^ n: heNaI Pk (n )<  И (            I          max ?J

В важном частном случае КИХ в виде кубических сплайнов, то есть для K =3, выражение (25) можно конкретизировать для практического использования, воспользовавшись явным выражением для многочлена p_K ( m ) из (23). Результаты представлены в таблице 2.

Таблица 2 – Допустимая длина входного сигнала в алгоритме модели CR для заданной максимальной погрешности А выходного сигнала

Допустимая погрешность А	Тип C/С++	Количество верных разрядов		Размеры сигнала
		десятичных	двоичных
1	float	7	23	215
	double	16	53	215 443
	long double	18	60	1000000
0,1	float	7	23	100
	double	16	53	100 000
	long double	18	60	464 158
0,01	float	7	23	46
	double	16	53	46 415
	long double	18	60	215 443

0,001	float	7	23	21
	double	16	53	21 544
	long double	18	60	100 000

Как видно из этой таблицы, форматов double и long double для вещественных чисел хватает для получения достаточно точных результатов ЛЛФ для сигналов с длиной до 100 000 отсчетов. То есть эти форматы годятся для использования в алгоритме модели CR для большинства реальных приложений.

Практические рекомендации по выбору КИХ

{ g h ( k )} , { g x ( k )} в алгоритме модели CR

Леммы 2 и 3, предложения 5-7 и следствие 2 позволяют сформулировать конструктивные правила, которых следует придерживаться при задании допустимых параметров алгоритма модели CR, в частности, отсчетов КИХ { g h ( k )} K 01 и { g x ( k )} K = 01 . Эти правила оформлены в виде следствия.

Следствие 3

( правила выбора КИХ ^{g (} к ^ K h o 01 , ^{g (} к ) K 01 ).

• -    Если в используемой ПЭВМ и операционной системе представление данных (сигналов, КИХ и др.) и операции с ними производятся абсолютно точно (например, заданы сигналы над GF ( p ) ), тогда выбор КИХ произволен и индуцированный алгоритм (модели CR) всегда является устойчивым.

• -    Если в используемой ПЭВМ и операционной системе либо представление данны х, либо операции с ними производятся с погрешностями (например, заданы сигналы над R или над C ), тогда для устойчивости индуцированного алгоритма модели CR выбор КИХ след ует ограничить. А именно: нули ПФ G x ( z ) , G h ( z ) должны быть расположены внутри или на границе единичной окружности Z -плоскости.

• -    В последнем случае, если хотя бы один из нулей расположен на границе единичной окружности Z -плоскости, тогда выбор формата представления вещественных чисел производится исходя из допустимой максимальной погрешности результата на основании предложений 6-7 и соотношения (25).

В простейших ситуациях для выбора формата представления вещественных чисел и определения максимально возможной длины обрабатываемых сигналов можно руководствоваться таблицей 2.

Заключение

Представлен анализ устойч ивости эфф ектив-ных алгоритмов ЛЛФ сигналов с по мощью двух спо собов. Первый из них использует трад иционно применяемый подход , основанный на анализе ПФ

ЛПП системы. Во втором способ е используется подход , осно ванный на анализе максимальной по -грешности выходного сигнала. Для второго спо -соба указаны допустимые длины входных сиг налов , обработка которых мо жет производ ить ся «устойч иво» эффективными алгоритмами с КИХ опред еленного типа.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (РФФИ), проекты: № 06-01-00616-а, 09-01-00434-а; российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта Президента РФ поддержки ведущих научны х школ (НШ-3086.2008.9) и Программы ф ундамен-тальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий», проект 2.12.