Анализ вероятностно-временных характеристик сети по доставке контента

Для большинства мультимедийных услуг критичными являются такие вероятностно-временные характеристики сети, как задержка пакета от пользователя до пользователя либо от сервера до пользователя, дисперсия задержки (джиттер), а также вероятность потери пакета. Под задачей обеспечения качества обслуживания, т. е. предоставления гарантий по параметрам качества обслуживания, как правило, понимается соблюдение заданных значений этих параметров.

Сейчас очень актуальна проблема задержек, возникающих в Интернете, из-за которых пользователю приходится долго ожидать появления необходимой ему информации. Это становится особенно заметным, когда необходимо получить различные виды мультимедиа. Основной причиной задержек является то, что Интернет представляет собой совокупность связанных между собой множества сетей. Прежде чем запрос о загрузке той или иной веб-страницы попадет на соответствующий веб-сайт, он может пересечь несколько сетей, в которых интернет-провайдеры в свою очередь принимают пакеты из чужих сетей. И здесь могут возникать большие очереди и сильное переполнение, что приводит к росту задержек и потере пакетов. Еще одной причиной возникновения задержек является недостаточная производительность серверов, на основе которых организуются информационные сайты, что приводит к значительному увеличению задержки и вероятности потерь пакетов. В результате возникает вопрос: а будут ли предоставлены гарантии по соблюдению параметров качества обслуживания, например, между пользователем и сервером?

Таким образом, очевидно, что обеспечение качества обслуживания требует внедрения как новых механизмов, так и методов построения сети Интернет.

Данные проблемы могут быть легко разрешимы при использовании сети по доставке контента CDN (Content Delivery Networks). Услуги такой сети основаны на кешированных решениях, предназначенных для перемещения информации ближе к конечным пользователям. Зеркаль- но отображая и кешируя файлы на большом количестве серверов, расположенных вдоль границы сети из коммутаторов и маршрутизаторов, эти службы стремятся приблизить данные к конечным пользователям, направить их на сайты, расположенные вдоль внешних, менее переполненных границ сети, предотвращая таким образом опасность сетевых заторов и осуществляя более быстрый доступ к информации.

Основная идея сети по доставке контента состоит в том, что в ее инфраструктуре основное внимание должно быть перенесено с сетевого уровня модели взаимодействия открытых систем на прикладной. Это означает, что функции устройств должны развиться от просто сборки и пересылки пакетов до сборки и пересылки необходимой информации. Данная сеть будет состоять из целого комплекса интеллектуальных устройств, совместно работающих для оптимальной доставки контента. Например, если происходит инициация запроса, то он будет направлен на устройство, которое предоставит лучшее обслуживание в данный момент и для данной информации. Каждый запрос будет обрабатываться уникальным образом, в зависимости от пользователя, местоположения и других факторов. Теперь не пользователь со своим приложением подстраивается под возможности сети, а сеть меняет свои настройки с учетом требований пользователя. При этом сеть не только реагирует на его текущие запросы, но и анализирует его предпочтения и текущее окружение, предоставляя соответствующую информацию системе управления, удовлетворяющей принципам адаптивности [2].

Поскольку каждое устройство в сети знает, где находится необходимая информация, то веб-страницы будут конструироваться из различных источников. Это позволяет устройствам специализироваться на определенных типах клиентов, таких как потоковое мультимедиа или постоянно изменяющиеся рыночные цены, а каждой странице – строиться в динамическом режиме. Здесь наиболее важным фактором является то, что в новой модели централизованному серверу, содержащему оригинал данных, нет необходимости обрабатывать каждый запрос, т. е. большая часть запросов будет обслуживаться в различных кеширующих устройствах [3].

Таким образом, сеть по доставке контента обеспечивает значительное снижение затрат на обслуживание и управление, экономию на вычислительных ресурсах и каналах связи, сокращение расходов на инфраструктуру, которая становится единой для всех типов приложений, т. е. данная сеть обеспечивает лучшее качество, большую надежность, а также возможность одновременного об- служивания большого количества запросов из любой точки земного шара.

В настоящее время существует множество методов для определения вероятностно-временных характеристик, например имитационное моделирование на ЭВМ, теория графов, теория массового обслуживания, алгебраические и теоретико-множественные методы, а также архитектуры «Интеллектуальные услуги IntServ и DiffSerf», но нет таких методов, которые бы позволили решать реальные сетевые задачи, характеризующиеся огромным количеством взаимодействующих узлов и разнообразием методов коммутации и сигнализации. Определение этих параметров является традиционно важной задачей в исследовании сетей связи и обмена данными, особенно при передаче различных видов мультимедиа, очень чувствительных к задержкам. Следовательно, нужно найти новый метод для определения данных параметров, который бы позволил находить их для любой сложности сети CDN и мог приспосабливаться к любым ее структурным изменениям.

В качестве такого метода может быть использована разработанная американским ученым и инженером Г. Кроном тензорная методология, опирающаяся на мощный аппарат тензорного исчисления и матричной алгебры. Применив тензорный метод для сложной сети массового обслуживания и используя понятия исходной и примитивной сети, можно получить выражения для определения характеристик исходной сети, задавая параметры для примитивной сети [4].

Для решения перечисленных выше задач воспользуемся контурным и узловым методами анализа тензорной методологии, которые позволяют решать различные сетевые задачи. В качестве примера рассмотрим известное выражение для определения загрузки устройств ρ, дающее связь между интенсивностью поступления вызовов λ и средним временем обслуживания tobsl. В частности, задавая среднее время обслуживания, загрузку устройств (для контурного метода) или интенсивность поступления вызовов (для узлового метода) для примитивной сети, мы можем получить распределения интенсивностей поступления вызовов (для контурного метода) и загрузки (для узлового метода) в исходной сети. Для подтверждения правильности результатов тензорного анализа дополнительно будем использовать результаты имитационного моделирования [5].

Рассмотрим частный случай сети, состоящей из тринадцати узлов и трех источников нагрузки (User) (пуассоновский поток) (рис. 1).

Системы массового обслуживания (СМО) обладают показательным распределением промежутков между вызовами (на рис. 1 оно обозначено как первая буква М) и показательной длительностью обслуживания (вторая буква М). Коммутаторы Switch и Content Switch (коммутатор контента) и маршрутизаторы Router рассматриваются как многоканальные системы с ожиданием (обозначено как буква V), кеширующие устройства (Cache) и серверы (Server) – как одноканальные системы с ожиданием (обозначены цифрой 1). Так как в качестве источников нагрузки рассматривается пуассоновский поток, то три источника нагрузки объединяем в один. Для экономии места на рис. 1 маршрутизаторы показаны в виде одной системы массового обслуживания. Буквой N обозначен объем использованного буфера.

В контурном методе выражение для загрузки устройств примет следующий вид: ρ=λ⋅ t _obsl . В исследуемой нами сети имеются семь контуров, и в качестве переменной принимается интенсивность потоков λ , протекающих в семи контурах сети (рис. 2).

В узловом методе для тринадцати ветвей сети, состоящей из тринадцати узловых пар (открытых путей), в качестве распределения потенциалов, которые возникают под действием поступающих в сеть потоков сообщений λ, принимаются величины загрузки устройств ρ , соответствующих ветвям сети (рис. 3). В узловом методе выражение для определения загрузки будет иметь вид λ = ρ⋅ t _obsl ^{- 1} , где t _obsl ^-1 =µ – интенсивность обслуживания запросов.

Зададим параметры примитивной сети для рассматриваемого нами случая (см. рис. 2, 3): среднее время обслуживания t _obsl, интенсивность поступления вызовов λ _prim для узлового метода и загрузку устройств ρ _prim для контурного метода (табл. 1).

В результате расчетов получим интенсивность поступления вызовов λ _ish и загрузку устройств ρ _ish для исходной сети (табл. 2).

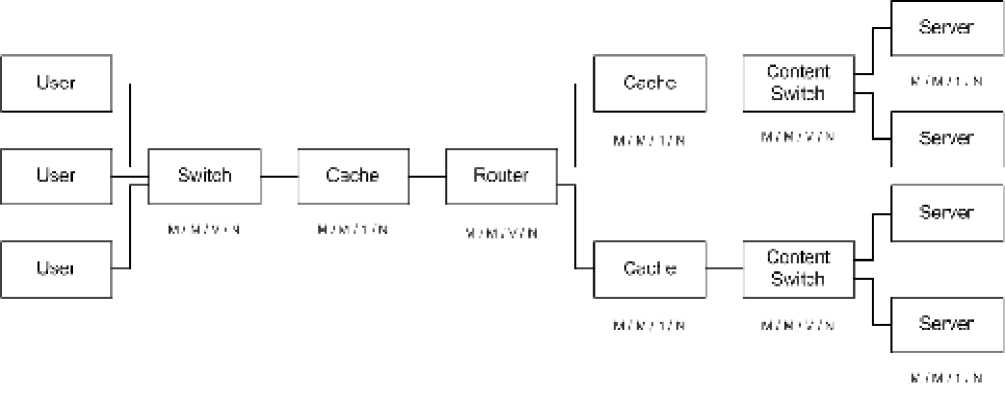
Рис. 1. Пример сети по доставке контента (обозначения см. в тексте)

По полученным результатам, в зависимости от поставленной задачи, определим необходимые параметры,

после чего найдем среднее время задержки для каждой СМО:

такие как задержка, вероятность потерь и т. д.

Покажем, как можно вычислить среднее время задержки для всей сети (для экономии места вывод формул не приводится).

Сначала определим среднюю очередь Q _СМО для каждой системы массового обслуживания:

T

CMO

QСМО

X

ish

⁺ t obsl .

S cmo

V + N

У n ■ n=V

p N ⁺ 2 V

■ V V

Далее определим среднее время задержки для всей сети.

Для частного случая сети, состоящей из тринадцати узлов, предположим, что запрос от пользователя идет через узлы 1, 2, 3, 9, 10, 11, 12, 13. Тогда результат для всей сети будет выглядеть следующим образом:

V !

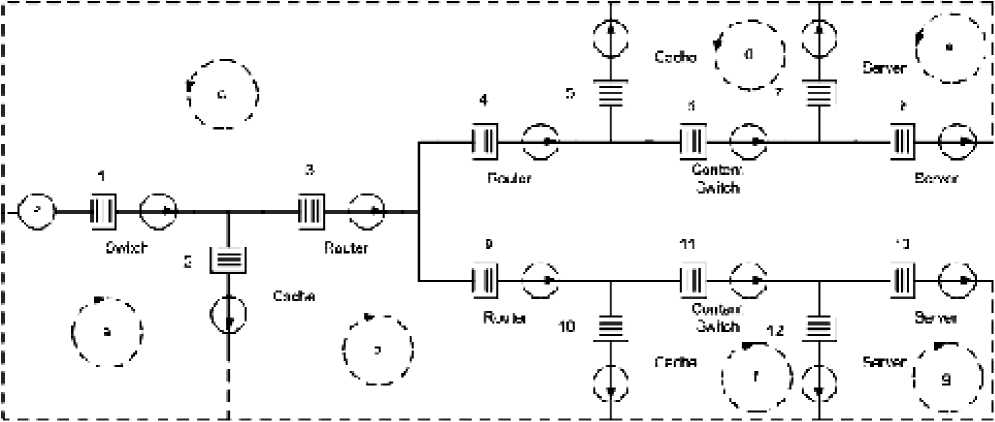
Рис. 2. Пример сети по доставке контента в тензорном виде для контурного метода

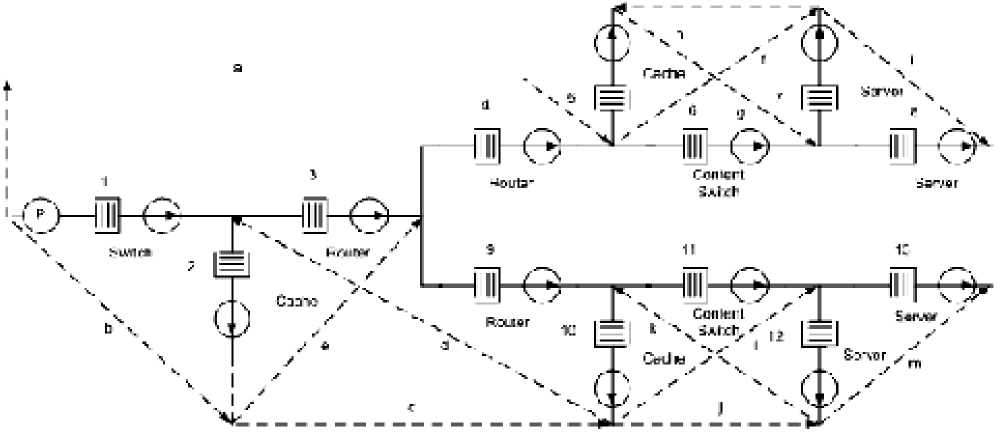
Рис. 3. Пример сети по доставке контента в тензорном виде для узлового метода

Таблица 1

Параметры для примитивной сети

Параметр	Номер узла
	1	2	3	4	5	6	7	8	9	10	11	12	13
t obsl 1,…, 13	0,50	0,60	0,90	0,80	0,70	0,40	0,30	0,70	0,80	0,90	0,50	0,60	0,40
λ prim 1,…, 13	0,23	1,73	0,95	0,73	0,78	0,36	0,54	0,86	1,80	1,54	0,60	0,90	0,85
ρ prim 1,…, 13	0,80	0,90	0,95	0,70	0,90	0,80	0,95	0,85	0,80	0,70	0,75	0,85	0,90

Т —Т            +

CMO ^CMO i ⁺ ^СМО 2 ⁺ ^СМО з ⁺

+ СМО 9 ⁺ ^СМОю ⁺ ^СМОи ⁺ -*СМО 12 ⁺ -^£СМО 13 '

Тензорный метод анализа позволяет быстро и надежно проводить анализ необходимых характеристик сетей по доставке контента, благодаря чему становится возможным эффективное управление распределением нагрузки во всей сети. Изменение вероятности перехода требования из одной ветви в другую в узле связи (для узлового метода) приведет к перераспределению нагрузки между отдельными ветвями сети, что в свою очередь изменит метрики и протоколы маршрутизации, на основе которых выбирается наиболее оптимальный маршрут.

Для иллюстрации этого положения рассмотрим схему на рис. 2. Пусть большая часть требований идет из источника нагрузки Р через ветви 1, 2, 3, 9 до ветви 10. Маршрутизация осуществляется на основе протоколов RIP/OSPF, которые выбирают кратчайший путь. В качестве метрики используется длина маршрута. Уменьшение вероятности перехода требований Р9,3 приведет к увеличению вероятности Р4,3 и перераспределению потоков, например, на маршрут 1, 2, 3, 4, 5, 6, 7. В результате произойдет сокращение загрузки и времени отклика устройств исходного маршрута, следовательно уменьшится вероятность потерь и задержка доставки пакетов в сети. В данном случае маршрутизация потоков осуществляется на основе протокола IGRP, в котором используется комбинация таких метрик, как задержка сети, полоса пропускания, надежность и загруженность сети.

Сравним результаты загрузки устройств, полученные выше с помощью тензорного анализа, с результатами имитационного моделирования.

В качестве исходных данных возьмем среднее время обслуживания в узлах сети t _obsl, интенсивность поступления вызовов X на источнике нагрузки Р, а также вероятности переходов из одного узла в другой P_{n , m} . Для проверки полученных результатов интенсивность поступления вызовов X на источнике нагрузки примем 0,23, равной X prim на первом узле тензорного анализа.

Приведем текст программы в системе GPSS для одной СМО M/M/N/K:

name3 table N$line3, 1 , 1, 140

name1 table N$line1, 1 , 1, 8

name2 table K$line2, 1, 1, 12

line3 STORAGE 140

line1 STORAGE 8

GENERATE (exponential (1, 0, 4.3))

ENTER line3

TABULATE name3

TEST LE K$line2, 12, poteri

QUEUE line2

ENTER line1

DEPART line2

ADVANCE (exponential (2, 0, 0.5))

LEAVE line1

TRANSFER,ex poteri SAVEVALUE 1, N$poteri ex LEAVE line3

TERMINATE

GENERATE 100000

TERMINATE 1

; Определение таблицы плотности распределения

; Проверка объема памяти для всех СМО

; Проверка объем памяти для данной СМО

; Создание запросов для ввода в процесс

; моделирования

; Занятие памяти или ожидание ее освобождения для

; всех СМО

; Обновление таблицы для всех СМО

; Проверка размера буфера. Если он занят, переход

; на метку «poteri»

; Постановка запроса в очередь

; Занятие памяти или ожидание ее освобождения для

; данной СМО

; Освобождение очереди

; Имитация обслуживания

; Освобождение памяти для данной СМО

; Безусловный переход на метку ex

; Сохранение потерь

; Освобождение памяти

; Блок таймера. Генерирование запросов и

; уменьшение их значения на 1

Программа для всей сети будет выглядеть как последовательность СМО с вероятностями перехода, указанными в табл. 3.

Результатом расчетов являются загрузка устройств с в сети по доставке контента (табл. 4).

Эти значения совпадают с результатами загрузки для исходной сети (см. табл. 2), что подтверждает правильность расчетов, проведенных тензорным методом.

Увеличение спроса на соединения с гарантированным уровнем качества сервиса (QoS) для доставки мультиме-

Таблица 2

Параметры для исходной сети

Параметр	Номер узла
	1	2	3	4	5	6	7	8	9	10	11	12	13
λish 1,…, 13	1,83	0,27	1,56	0,78	0,04	0,73	0,36	0,36	1,78	0,04	0,73	0,78	0,04
ρ ish 1,…, 13	0,20	0,03	0,17	0,08	0,01	0,08	0,04	0,04	0,80	0,01	0,08	0,04	0,04

Таблица 3

Вероятности переходов из одного узла в другой

Параметр P3,1 P4,3 P6,4 P8,6 P11,9 P13,11 Значение 0,70 0,43 0,69 0,50 0,76 0,50 диаданных, таких как потоковая передача мультимедиа в реальном масштабе времени, подталкивают к развитию новых принципов построения сети Интернет, а также методов анализа качественных показателей, которые бы позволили предоставлять эти услуги с максимальным качеством. В данной статье была рассмотрена сеть по доставке контента как наиболее перспективное направление сетей нового поколения, которое способно более быстро и эффективно доставлять информацию конечным пользователям.

Тензорный метод анализа позволяет не только быстро и надежно проводить анализ вероятностно-временных характеристик сетей связи, вне зависимости от структуры сети и ее сложности, но и приспособиться к любым изменениям в сети, повышая эффективность ее работы.

Тензорная методология существенно упрощает расчеты параметров качества обслуживания и помогает решать задачи для сложных топологий сетей, где другие методы требуют больших вычислительных ресурсов или не могут получить решения из-за сложности задачи. Данный метод позволяет легко производить расчет характеристик таких систем, их проектирование, управление, предвидеть последствия тех или иных изменений в сети, оптимизировать работу систем и т. д., причем решения могут быть получены для любой структуры сети, что было невозможно сделать применявшимися ранее методами теории массового обслуживания, теории графов и т. д. Как было показано выше, с помощью тензорного метода можно менять вероятность перехода тре- бований из одной ветви в другую, что позволяет оптимизировать такие важные параметры сети, как задержка доставки пакетов, вероятность их потерь, загруженность сети и т. д.