Анализ влияния дискретности цифрового регулятора положения на точность воспроизведения сигнала задания в позиционно-следящем электроприводе

на точность воспроизведения сигнала задания. Дискретность определяется экстраполятором нулевого порядка, входящего в состав цифроаналогового преобразователя (ЦАП) цифрового регулятора положения (ЦРП).

Расчетная структурная схема САУ настроенная на технический оптимум [4] показана на рис. 1. Дискретность ЦРП, вносимая экстрапо-лятором, будем оценивать относительно непрерывной САУ, которая служит эталоном.

Рис. 1. Структурная схема электропривода

Оценка погрешности, вносимая экстраполя-тором, является важной составляющей в погрешности воспроизведения заданной траектории движения электропривода Хзд (р). Это особенно важно для прецизионных позиционно следящих электроприводов, которыми оснащаются, например, координатно-расточные станки особо высокой точности. Например для станков класса С при перемещениях подвижного органа станка до 1250 мм погрешность должна составлять до 2 мкм [5]. При обработке сложной поверхности следящий электропривод должен воспроизводить гармонический сигнал [6]. При этом в процессе обработки нужно поддерживать постоянную скорость подачи инструмента (VЗД), заданную для данного технологического процесса. Связь между круговой частотой юЗД, VЗД и ХЗД устанавливается зависимостью:

Ю зд = \.   .                 (1)

Х зд

W ₅ ( z ) =

6 ( z ) X зд ( z )

___________________ ⁽ z ^{- 1)(} z ^{- d} ) ___________________ ₍₄₎ ( z - 1)( z - d ) + K [ z ( Т РП - T + T 1 d ) + T 1 (\ - d ) - dT_pn ] . ⁽⁴⁾

Анализ погрешности, вносимый экстрапо-лятором нулевого порядка, будем проводить с помощью передаточной функции системы по ошибке в форме Z-преобразования с последующим переходом в область псевдочастот X с использованием билинейного преобразования

Аналитическое исследование зависимости (4) в общем виде не представляется возможным. Поэтому используем численный метод для оценки погрешности вносимой экстраполятором. Дадим ряд значений периода дискретности T_РП, которые 2 n определяют частоту квантования ( У ₀ = —— : Т РП ^{Т РП}

_ 1 + w

Z =---- [7]. Это в свою очередь позволяет ис-

1 - w

пользовать логарифмические амплитудно-фазо-

вые частотные характеристики для исследования

системы. Передаточная функция по ошибке в

форме Z-преобразования имеет вид:

W ₃ ( z ) =

6 ( z ) X зд ( z )

.

1 + W p ( z )

В (2) передаточная функция системы в форме Z-преобразования в разомкнутом состоянии

представлена зависимостью:

W p ( z ) =

K [ z ( Т РП - T 1 + T 1 d ) + T 1 (1 - d ) - dT_pn ] ^{( z} - ^{1)( z} - d )

. (3)

В (3) принято: К – коэффициент передачи системы, TРП – период дискретности регулятора положения привода подачи прецизионного - ТРП станка, d = e T1 , T1- постоянная времени апериодического звена. С учетом (3) зависимость (2) представим в виде:

=0,04 с; TРП=0,08 с; TРП=0,16 с; TРП=0,3 с; TРП=0,4 с.

Результаты расчетов сведены в табл. 1.

Логарифмическая амплитудно-частотная характеристика аналоговой САУ, принятой за эталон определяются передаточной функцией: _{W (} м = 6 ( Р ) =     1     = 0,147 p (0,08 p + 1)

р Х зд ( Р ) 1 + W p ( p ) 0,012 p ² + 0,147 p + 1.

На основании полученного выражения проведем расчет необходимых параметров для построения ЛАФЧХ:

20 1g 0,147 =- 16,8дб;

to, = -^— = 12,5c ^{- 1}; 1g12,5 = 1,1дек

• ¹    0,08

to₂ = —— = 9,17c ^{- 1};1g9,17 = 0,96дек^.

• ²    0,109

По расчетным данным табл. 1 и аналоговой системы на рис. 2 представлена логарифмическая амплитудно-частотная характеристика по ошибке позиционно-следящего электропривода.

Анализ амплитудно-частотной характеристики показывает, что при увеличении периода

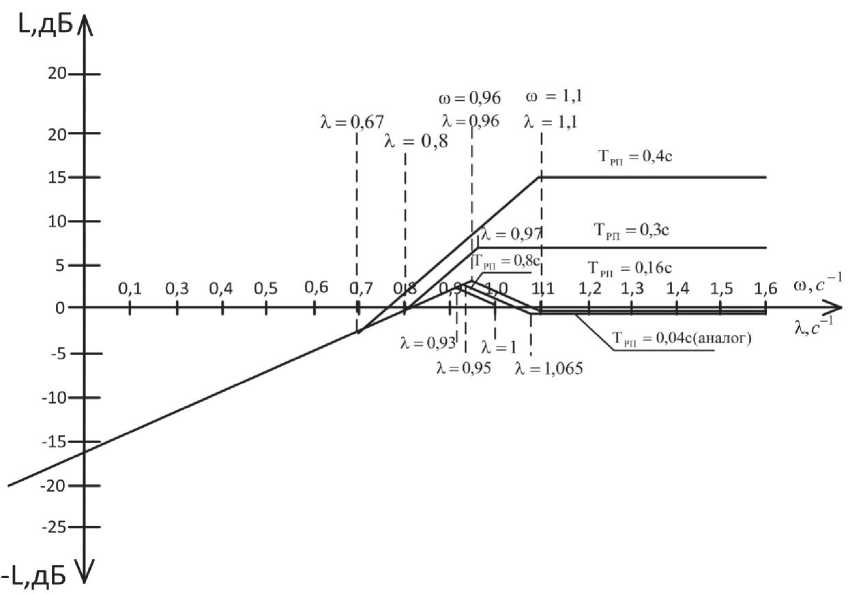
Рис. 2. Логарифмическая амплитудно-частотная характеристика по ошибке

Таблица 1. Результаты расчетов

Период дискретности регулятора положения Т с 1 РП ,с	Передаточная функция разомкнутой системы W p ( Z ) = "(zT"A x зд ( z )	Передаточная функция по ошибке системы W 5 ( W )= ^7 x зд ( z )	Амплитудно - фазовая частотная характеристика системы по ошибке т W 5 (J X '2) X, с -1 ; X ,дек; К, дб; ТРП ,c.
0,04	0,05(1,1 Z + 1) ( Z - 1)( Z - 0,6)	Z - 0,6	0,147 j Х (1 + j X 0,08)       = 0 08; 0,0116 2 ( j X )2 + 0,125 jХ + 1 1 T 2 = 0,108. X, = 1 = 12,5; lg12,5 = 1,1. с = 0,58 1    T 1 X2 = ± = 9,26; lg9,26 = 0,966. 2    Т 2 20lg К = 20lg 0,147 = -16,8
		0,0544( Z +1) + ( Z - 0,6) z -1
0,08	0,143(1,39 Z +1) ( Z - 1)( Z - 0,366)	Z - 0,366	0,147 j Х (1 + j Х 0,086) ---------------------------- T = 0,086; 0,112 2 ( j X )2 + 0,1136 j X + 1 T 2 = 0,112. X= 1 = 11,63; lg 11,63 = 1,06. 1    T 1 с = 0,52 X2 = ± = 8,93; lg8,93 = 0,95. 2    Т 2 20lg К = 20lg0,147 = -16,8
		1 37Z + 1 ( Z - 0,366) + 0,145( ,     ) ) Z -1
0,16	0,325(1,88 Z +1) ( Z - 1)( Z - 0,134)	Z - 0,134	0,147 j X (1 + j X 0,1)     T = 01 0,116 2 ( j X )2 + 0,092 j X + 1 1   ” T 2 = 0,116. X, = 1 = 10; lg10 = 1. с = 0,4 1    T 1 X2= ± = 8,62; lg8,6 = 0,93. 2    Т 2 20lg К = 20lg0,147 = -16,8
		( Z - 0,134) + 0,326( 1,8 Z5Z 1 + 1 )
0,3	0,48(3,097 Z +1)	Z - 0,023	0,146 j X(1 + j X0,157)    T = 0 157. 0,1092( j X)2 + 0,075 j X +1 1 T 2 = 0,108. X, = — = 6,37; lg 6,37 = 0,8. с = 0,347 1    T 1 X2 = — = 9,26; lg9,26 = 0,96■ 2    Т 2 20 lg К = 20lg0,146 = -16,8
	( Z - 1)( Z - 0,023)	3 09Z +1 ( Z - 0,023) + 0,48(3— Z —1) z -1
0,4	0,52(4,21 Z + 1)	Z - 0,0066	0,147 j X (1 + j X 0,2)      T = 0 2; 0,069 2 ( j X )2 + 0,069 j X + 1 1 T2 = 0,069. X, = 1 = 5; lg5 = 0,7. с = 0,347 1    T 1 X2= -1- = 14,5; lg14,5 = 1,16 2    Т 2 20lg К = 20lg0,147 = -16,8
	( Z - 1)( Z - 0,0066)	( Z - 0,0066) + 0,52( 4,21 Z + 1 ) Z -1
0,5			Система неустойчива

дискретности регулятора положения, существенно возрастает динамическая ошибка в воспроизведении заданной траектории движения. Это особенно важно для приводов прецизионных КРС класс С. Для КРС особо высокой точности при обработке сложных профилей с закруглениями предъявляются вполне определенные требования по скоростям движения приводов подачи [6].

Заметим, что при TРП=0,04 с или имеем хорошее совпадение с погрешностью аналоговой системы, которая при заданных параметрах имеет полосу пропускания в разомкнутом состоянии          ,             . По этому хорошее совпадение дискретной системы с непрерывным аналогом реализуется, если :

^  157

---=---= 11,2 . Поэтому для достижения вы- 2 ю с   14

сокой точности необходимо, чтобы в 12 раз.

Моделирование системы в среде Matlab подтверждает полученные расчетным путем выводы. Графики отклонения ошибки 5 (t) дискретной системы от аналогового прототипа показаны на рис. 3 при входном воздействии 1(t) .

Основываясь на проведённое теоретическое исследование был разработан алгоритм автоматического изменения периода T _РП в зависимости от диаметра воспроизводимой окружности и линейной скорости её обхода. Очевидно, что с увеличением значения периода T _РП будет снижаться точность воспроизведения криволинейных траекторий подвижными органами станка. Чрезмерное уменьшение T _РП вызовет неоправданный расход процессорного времени ЧПУ. Алгоритм позволяют выбрать наиболее оптимальное значение периода T _РП при котором обеспечивается требуемая точность воспроизведения окружности.

Экспериментальные исследования, подтверждающие эффективность разработанного алгоритма, проведены на прецизионном координатно-расточном станке модели 2440СФ4 с УЧПУ NC-310 фирмы «Балт-Систем». В качестве измерительных элементов положения стола и салазок использовались фотооптические инкрементальные линейки типа ЛИР-7 фирмы СКБИС. Точность данных фотооптических линеек – 0,5 мкм. Каждая интерполирующая координата исследуемого стенда-станка прошла процедуру юстировки, которая обеспечивает точность позиционирования подвижного органа на уровне 2,5 мкм, что соответствует классу точности С.

Описанное в данной статье экспериментальное исследование проводилось при программном задании отработки эталонных траекторий, в качестве которых использовались эталонные окружности диаметром 2 мм, 4 мм, 6 мм, 8 мм и 10мм. Линейная скорость обхода всех эталонных окружностей постоянна и равняется V _ЭО =1000 мм/мин.

Учитывая дискретную природу САУ ПМС, для дальнейшей математической обработки результатов эксперимента, каждую эталонную окружность целесообразно представить в виде одномерной матрицы R _ЭО. Любой элемент данной матрицы представляет собой мгновенный радиус эталонной окружности на i-том шаге интерполяции. Размерность данной матрицы находится как:

R - °Э0

, где VЭО – линейная скорость отработки эталонной окружности, DЭО – диаметр эталонной окружности, TИ – такт интерполятора УЧПУ.

Значение каждого элемента матрицы R _ЭО определяется по следующей формуле:

R - °Э0

R30t- —

.

Для оценки реально полученной траектории использовался независимый цифровой самописец (НЦС), который считывает данные с линейки

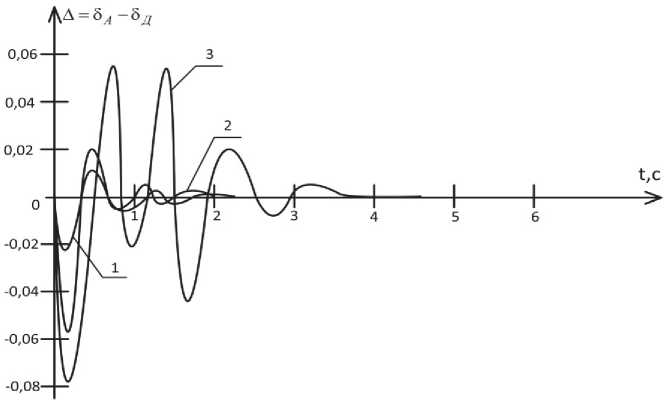
Рис. 3. Отклонение ошибки 5 (t) дискретной системы от аналогового прототипа: кривая 1 – T_РП= 0,04 с; кривая 2 – T_РП = 0,08 с; кривая 3 – T_РП = 0,16 с

стола и линейки салазок. Полученная с НЦС при отработке эталонной окружности одномерная матрица данных характеризует реально полученную окружность, указанную матрицу обозначим как R _РО. Значение каждого элемента данной матрицы представляет собой мгновенный радиус реально полученной окружности на i -том шаге интерполяции и находится как:

Rpo^Jx^ + Y^ , где Xi – мгновенное значение, считанное НЦС с линейки стола на i-том шаге интерполяции, Yi – мгновенное значение, считанное НЦС с линейки салазок на i-том шаге интерполяции.

Матрица, полученная в результате вычитания одноименных элементов матрицы R _ЭО и матрицы R _РО, является по существу динамической погрешностью ∆ _ЭО воспроизведения эталонной окружности, которая и характеризует качество воспроизведения заданной траектории подвижными органами прецизионного металлорежущего станка:

^ЭО = ^ЭО — ^PO .

Элемент ∆ _{ЭО MAX} матрицы ∆ _ЭО, имеющий максимальное значение, является максимальным значением погрешности воспроизведения эталонной окружности.

Блок-схема алгоритма экспериментального определения значения ∆ _{ЭО MAX} представлена на рисунке 4. Используя вышеупомянутый алгоритм, а также задаваясь рядом значений T _РП в диапазоне 10-80 мс для эталонной окружности определим зависимость ^30 MAX — fOW) ^.

Для получения достоверных результатов проводилось трёхкратное экспериментальное определение зависимости [8].

Заметим, что матрицы R _РО и R _ЭО имеют одинаковую размерность

Период T _РП в УЧПУ NC-310 определяется параметром servo_tick инструкции CAS.

Такт интерполятора T _И – параметром int_tick, причём T _И =1 мс=const.

Результат эксперимента представлен в виде се-мействаграфиков зависимости ^30 MAX — fO'pn) для эталонных окружностей диаметром 2 мм, 4 мм, 6 мм, 8 мм и 10 мм, при линейной скорости обхода V _ЭО =1000 мм/мин (см. рис. 5). Из анализа представленных выше графиков следует возможность выбора такого значения T _РП, при котором обеспечивается требуемая величина максимальной погрешности ∆ _{ЭО MAX} .

По полученным данным можно сформулировать следующие выводы, если линейный прототип удовлетворяет техническим требованиям по ошибке воспроизведения заданной траектории, то дискретный регулятор может внести дополнительную погрешность, что может привести к увеличению погрешности и неудовлетворению технических требований. В этом случае требуется либо увели- чить частоту ω0 экстраполятора, либо увеличить быстродействие аналоговой части системы.

Экспериментально подтверждено теоретическое положение о необходимости обеспечения неравенства - > 12,5 ...20 для обеспечения c точности воспроизведения заданной траектории движения по классу точности C.

Экспериментально доказана возможность повышения точности воспроизведения окружности при снижении общей вычислительной нагрузки на микропроцессор УЧПУ за счёт применения алгоритма автоматического изменения периода T_РП в зависимости от диаметра воспроизводимой окружности и линейной скорости её обхода.