Анализ влияния гравитационных и капиллярных сил на двухфазную фильтрацию жидкости

Моделирование месторождений является одной из многих современных технологий, используемых при разработке и добыче нефти. Оно используется для сравнения различных механизмов добычи и предоставляет базу для экономического анализа потенциальных сценариев подготовки месторождения. Существующие коммерческие программные пакеты для проведения моделирования представляют собой широкий набор инженерных средств, обеспечивающих принятие оптимального решения в управлении месторождением. Однако точность выдаваемых ими прогнозов в большой степени зависит от разрешающей способности модели. Из-за существующих вычислительных ограничений вы-сокодетализированную сетку геологической модели подвергают осреднению до сетки с сотнями тысяч блоков. По этой причине необходимо аналитическое решение, которое дает возможность определить процент ошибки в решении задач численными методами.

В данной статье показано, насколько существенно влияют на результаты моделирования число слоев, различия в плотности флюидов, отношение вертикальной и горизонтальной проницаемостей, даже при одномерной фильтрации двухфазной жидкости. Различия будут более существенными при 3-D моделировании многокомпонентной смеси. Важным в этой работе является определение условий, при которых основной компонентой течения является поток, индуцированный гравитационной составляющей.

Постановка задачи

Дана вертикальная трубка S = const, заполненная пористой средой, с перегородкой в сечении О-О. Выше сечения О-О находится тяжелая жидкость – вода, ниже более легкая – нефть или газ, который в первом приближении считается несжимаемым. В какой-то момент перегородка О-О убирается. Требуется рассмотреть, как будет всплывать нефть и опускаться вода [1].

Математическая модель

Распишем основные уравнения двухфазной фильтрации в поле массовых сил [2]. Закон Дарси:

Q 1

k k * ( ⁵ )

Ц i

d p d x

P i

X

) 5 ( x ) , Q 2

- k k < >  fd p       ^ A 5 ( x )

Ц 2 Id x ^{P 2} V ’

Уравнение неразрывности:

5 Q,

-^m = mS (x)

8 x8t

⁸ Q 2 о , . 8 ( 1 - 5 ) (2) -----  = mS ( x ) —------- V V

8 x                   8 1

где Q – дебит i -той фазы; р – давление i -той фазы; k _i* – относительные фазовые проницаемости; ρ _i – плотность I -той фазы; μ _i – вязкость i -той фазы; s – водонасыщенность; k – проницаемость; m – пористость; t – время; X – проекция ускорения массовых сил на направление течения; S(x) – площадь сечения.

Система уравнений (1), (2) по известной теории Баклея-Леверетта [3] преобразуется к виду:

mS(x) ^ L +

^d f

Q (t)    + v (x) s (x )^La d 5                  d 5

8 5 + d x

Г , x d 5 \ d S с , X 8 V f ,^{( 5} ) V ^{( x} ) ^+ ^{5 ( x}

^{J 1}               8 x             8 x

=0 (3)

Система дифференциальных характеристик уравнения (3) имеет вид:

Н.Р. Кондратьева. Анализ влияния гравитационных и капиллярных сил на двухфазную фильтрацию жидкости dt                   dx              =(4),

--------=  - mS (x)                           d f           Г      55d

Q (t) If + v (X) s (X )^p f As) [ V (x) 77 + S (x) 77 ] d s где f1(s) =    k * (s) k 2 (s)   - функция Баклея-Леверетта, v (x) _ kA ^X - величина, имеющая размерность

M оk *(s) + k 2(s)

скорости.

Суммарный расход воды и нефти через любое сечение равен 0, тогда из (4) получим:

dt                dx(5)

mS ( x ) ” V ( x ) S ( x ) f ‘ ( s )

Для данной задачи будем рассматривать следующий вид фазовых проницаемостей: k 1 *(s) = S ² , k 2 *(s) = (1-S).

Из (5) следует _x _ K G x ! f ' ( _s ) t . Следовательно, вычисляя фронтовые насыщенности S ф1 и S ф ₂ и m ¹

определяя значения f'1(Sф1) и f'1(Sф2), можно найти положение фронтов в любой момент времени. На рис. 1 показано примерное распределение водонасыщенности в последующие моменты времени.

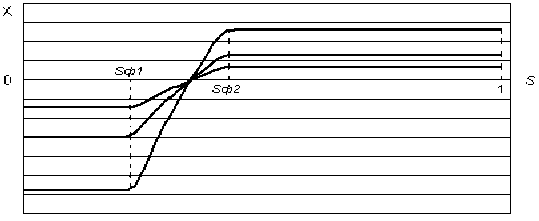
Рис. 1. Распределение водонасыщенности по глубине

Аналитическое решение свидетельствует о полном замещении флюидов, причем этот процесс происходит постепенно. В гидродинамическом симуляторе Eclipse Version 2004A_1 была смоделирована аналогичная ситуация. Начальные условия в модели – явное задание давления и водонасыщен-ности, граничные условия - непроницаемые границы, d p _ Q . При моделировании рассматривалось d n разное количество слоев, 2, 6, 10, 16 и 20, для выбора наиболее оптимального числа, при котором распределение насыщенности максимально приближено к распределению, полученному в аналитическом решении. Помимо этого, важно знать влияние всех механизмов на поток: разницу плотностей воды ρw и нефти ρ0, проницаемостей в вертикальном Kv и горизонтальном направлении KH и т.п. По расчетам симулятора получены следующие результаты: здесь t= t – безразмерное время, T – харак- терное время моделирования.

Модель №1. Параметры модели: Δ ρ = ρ w – ρ 0 = (1000-870)кг/м ³ ; K v /K H = 10/100.

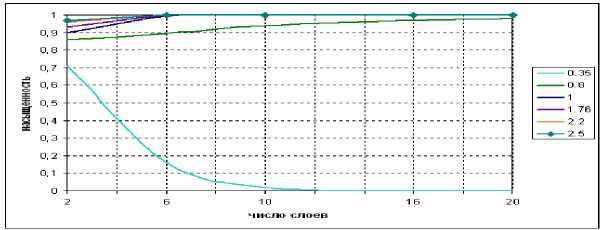
Рис. 2. Распределение нефтенасыщенности в зависимости от времени. Значение на первом слое

По результатам моделирования можно судить о наиболее значимых параметрах, которые будут обеспечивать поперечную фильтрацию в модели. Изменение отношения вертикальной проницаемо- сти к горизонтальной оказало более сильное влияние на распределение водонасыщенности, чем изменение плотности. И, конечно, важным параметром в модели является число слоев.

Модель №2. Параметры модели: Δ ρ = ρ w – ρ 0 = (1200-870)кг/м ³ ; K v /K H = 10/100.

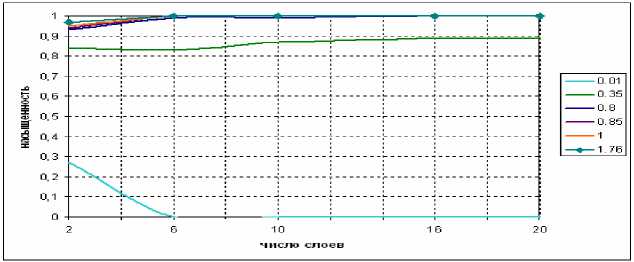
Рис. 3. Распределение нефтенасыщенности в зависимости от времени. Значение на первом слое

Задача для двухфазного потока в двумерном поперечном сечении

Рассмотрим влияние эффекта гравитации в более общем случае, а именно двухфазный поток в двумерном поперечном сечении. Уравнения материального баланса для несжимаемого потока:

m ⁸ s w + ⁸ U w + ⁸ V w = 0, — (u +U ) + — (V + V ) = ⁰            (6)

8 T      8 X       8 Y         8 X      w o 8 y ^w ' o'

Скорость фильтрации из уравнения Дарси для обеих фаз будет:

8 p ,                             8 P

U j-- k h⁽ X , Y ⁾ k j ax V j-- k v⁽ X , Y ) k j p j                               p j

Граничные условия V 0 = V w = 0 при у = 0 и у = Н, P 0 , P w – константы при х = 0 и х = L, где Р j -давление в фазе j , U j V j , скорости соответствующих фаз в вертикальных и горизонтальных направлениях, K ν (X, Y) и K k (X, Y) – функции распределения абсолютной проницаемости в вертикальных и горизонтальных направлениях, K _r j – функции относительных фазовых проницаемостей фазы j , μ j – вязкость фазы j .

Введем безразмерные переменные:

χ = X/L, y = Y/H, t = Tq/L, и j = U j /q, ν j = LV j /qH, k ν = k aν K v (x, y), k h = k ah K H (x, y), p j = P j k ah /L q μ 0 и λj = k rj μ o /μ j . Здесь K v (x, y) и K H (x, y) – безразмерные функции распределения проницаемостей в вертикальном и горизонтальном направлениях, q- суммарный расход .

Обозначим (L/H) ² ∙ k ν / k aν = R l ² . Связь между P 0 и P w установим, используя определение капиллярного давления и учитывая эффект гравитации.

В результате имеем:

„ 2 ⁸ P o               ⁽ V o ⁺ V w )        ₊ X w ( L k V P *      8 J L k av A p g ) ,               ⁽⁸⁾

R l ⁸ y K v ( ^ • y )( X o + X w ) ( X o + X w ) h ^г q p _XK . ⁸ y Hq p o

Обозначим: М= X w , n = L k av ^{A p g} , n = L k p c .

X o gv      Hq Po cv H 2 q Po

N gv , N cv , – безразмерные параметры, характеризующие влияние гравитационных и капиллярных сил на двухфазную фильтрацию.

Тогда, если выполняются условия ^M N ^gv >>1, N gv >>  N cv , уравнение (8) можно использовать для (1 + M )

описания фильтрации при доминировании гравитационных сил.

Заключение

Исходя из аналитического решения можно сделать вывод о том, что при данных условиях изменение насыщенности происходит постепенно. В 2-слойной модели насыщенность меняется плавно, без резких скачков, чего невозможно добиться в модели с большим количеством слоев. В однослойной модели проследить движение флюида при данных условиях вообще не представляется возможным. Одним из основных параметров, обеспечивающих поток в вертикальном направлении, является отношение длины пласта к его толщине, а также отношение латеральной и горизонтальной проницаемостей.

По результатам развернутого аналитического решения можно говорить о том, что в пористой среде движение флюидов будет происходить под действием сил тяжести, когда результирующая вязко- стных, гравитационных и капиллярных сил определится модифицированным безразмерным гравитационным числом. Аналитическое решение и численное моделирование при выполнении ряда условий показали существенное влияние гравитационных сил на поведение системы.