Анализ влияния коэффициента нелинейности на неустойчивость частотных характеристик колебательного контура при силовом резонансе с использованием пакета прикладных программ MATLAB

Введение. Анализируя результаты разных технологий формирования колебательных процессов в электрических цепях, необходимо отметить, что одним из сложнейших аспектов, влияющих на их стабильность, являются типы внешних воздействий.

Структурно эти воздействия можно разделить на два типа: силовое и параметрическое.

Классическим примером силового воздействия на LC -контур является включённый в цепь контура генератор. Он задаёт колебания на некоторой частоте р с возникновением вынужденных колебаний в LC -контуре.

В случае применения для генерации колебаний колебательного контура на базе силового резонанса точность характеристик колебательного контура обуславливает точность свойств генерируемых колебаний. Анализируя выходные характеристики реального колебательного контура при силовом резонансе на широком диапазоне частот от резонансной частоты, были обнаружены следующие особенности:

• 1)    максимальное значение амплитуды не соответствует расчётной резонансной частоте колебательного контура;

• 2)    на граничных частотах полосы пропускания возникает неоднозначность значения амплитуды колебаний.

Что стоит за этими особенностями? Какие процессы в цепи не учитываются, но существенно влияют на значения амплитудно-частотной характеристики (АЧХ), рассмотрим ниже.

Основная часть. Для изучения вышеуказанных особенностей были проведены математические расчёты и программное моделирование АЧХ колебательного контура с помощью пакета прикладных программ для решения технических задач MATLAB.

Математический расчёт. Колебательный контур является нелинейной системой, поэтому рассмотрим, для удобства, поведение слабо нелинейной системы при силовом резонансе и при приближении малых значений: трёх М – малая нелинейность, малая диссипация и малая амплитуда.

К этим трём М , приводящих к затуханию колебаний, добавим ещё и гармоническую внешнюю силу P ₀cos( pt ). Три М будут иметь отрицательное значение, а внешняя гармоническая сила – положительное, таким образом уравнение для колебательного контура будет иметь вид (1):

q+w^q = -F(q,*q) + P0cos(pt),

где q – значение заряда и его производные ^q, Q ) , ω 0 – циклическая резонансная частота колебательного контура, F(q,q) – коэффициент малая нелинейность, малая диссипация и малая амплитуда, P ₀cos( pt ) – гармоническая внешняя сила с амплитудой P ₀ и частотой воздействия p .

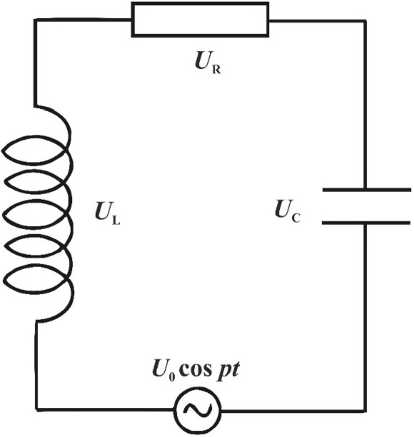
Рис. 1. Колебательный контур

Fig. 1. Oscillatory circuit

Для решения (1) используем метод гармонического баланса (МГБ). Но для начала проведём ряд преобразований уравнения. Согласно второму закону Кирхгофа, общая сумма падения напряжения на элементах системы (рис. 1) будет равна напряжению от внешнего источника колебаний (2):

U_c + U_R + U_L = U_o cos pt, (2)

где Uc , UR , UL – значения падения напряжения на конденсаторе, нагрузке и индуктивности соответственно, U ₀cos pt – общее значение падения напряжения в цепи, подключенной к переменному току.

Распишем более подробно падение напряжений на элементах контура, кроме падения пряжения на ёмкости, так как будем далее рассматривать нелинейную функцию заряда:

на-

ку-

d2q dq

L —— + R — + Uc = Uo cos pt, dt2 dt c 0 p где L – индуктивность контура, R – активное сопротивление контура, q – значение заряда.

Разделим выражение 6 на L и получим (4):

q + 2.6q + to^q + yq3 = ?o cos Rt>

.. d2q RU где        ,       – два декремента затухания,               – линейное слагаемое и и0

.

бическая нелинейность, ^{Ро =} Т

Ucq

Более подробная трансформация выражения выглядит следующим образом: U(:= —, LC

Uc _ 4 где C ™-™.~ ™™m„- m.^.™ „ 1 - z следовательно, →        , где C 0 – это среднее значение емкости, а , Z, - Ш0 есть цикли- ческая частота собственных гармонических колебаний. В выражении (4) есть слагаемое γq3, которое необходимо для отражения наличия дополнительных гармоник, возникающих в кон- денсаторе при колебательном процессе. В результате выражение приобретает вид (5):

у = ^q +yq³.                                          (5)

Для решения уравнения (4), как дифференциального уравнения 2-го порядка, общий подход не применим. Наиболее наглядным и информативным способом решения будет – МГБ.

Решение через МГБ уравнения (4) будет определяться в виде суммы гармоник одной частоты, но разных амплитуд:

q = acos(pt) + bsin(pt),                                            (6)

где a и b малые коэффициенты при гармонических функциях.

Результатом решения уравнения (4) будет известное выражение для резонанса в обычных линейных системах:

(to2 — p2)2 + 452p2’ гдеw2 =ш2+-уА2будет являться поправкой, учитывающей влияние нелинейности элемен- тов цепи контура LC. Аналитическим результатом изучения формулы (7) будет график рис. 2.

Анализируя полученный теоретический график АЧХ реального колебательного контура при силовом резонансе на широком диапазоне частот от резонансной частоты, были обнаружены следующие физические явления:

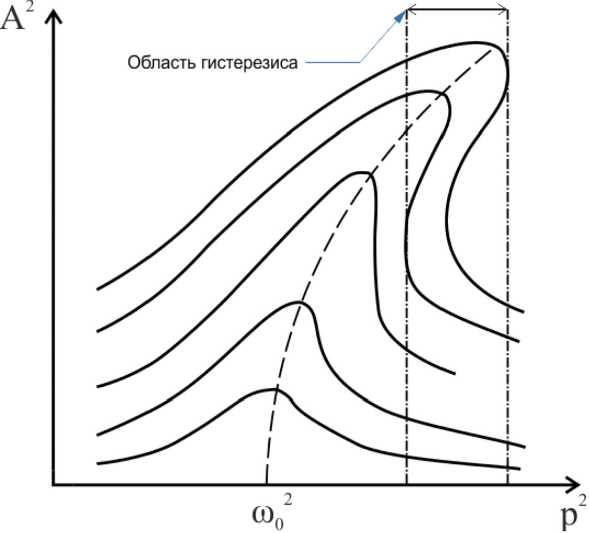
Рис. 2. Аналитический график АЧХ реального колебательного контура

Fig. 2. Analytical graph of the amplitude-frequency response of a real oscillatory circuit

• 1)    отличие резонансной частоты колебательного контура от расчетной;

• 2)    неоднозначность амплитуды колебаний на граничных частотах полосы пропускания;

• 3)    увеличение амплитуды внешнего воздействия, с увеличением области неоднозначности амплитуд;

• 4)    наблюдение в правой части аналитического графика неоднозначности частот с появлением «петли гистерезиса».

Компьютерное моделирование. Для анализа выражения (7) в среде MATLAB была написана программа для расчета АЧХ контура LC с известными входными параметрами: входное напряжение U = 27 В, индуктивность контура L = 24 мкГн, резонансная частота контура ω 0 , соответствующая новому программному обозначению циклической частоты w0 = 500 Гц, диапазон расчётов p = 2000 Гц, коэффициент затухания δ , соответствующий обозначению d = 100, коэффициент нелинейности γ , соответствующий обозначению y = 300000.

U = 27;%Амплитуда внешнего воздействия, В

L = 24*10^(–6);%Индуктивность колебательного контура, Гн w0 = 2*pi*500;%Резонансная частота, Гц p = 2*pi*0:0.01:2*pi*2000;%Диапазон частот внешнего воздействия d = 100;%Коэффициент затухания y = 300000;%Коэффициент нелинейности емкости

Рассчитаем числитель выражения (4):

P = U/L.

Создадим нулевую матрицу длинной, равной количеству отсчётов p, рассчитаем первый отсчёт и зададим изначальный уровень максимальной амплитуды mA = 0:

A = zeros(1, length(p));

A(1) = P^2/((w0^2-p(1)^2)^2+4*d^2*p(1)^2);

w1 = w0^2+3/4*y*A(1);

mA = 0;

Для непосредственного расчёта выражения (4) при каждом значении пропишем цикл с повторением, равным количеству отсчётов диапазона измерения. При этом с увеличением амплитуды будем присваивать новые значения для mA с условием превышения предыдущего значения:

for i = 2: length(p)

A(i) = P^2/((w1-p(i)^2)^2+4*d^2*p(i)^2);

w1 = w0^2+3/4*y*A(i);

if mA<=A(i)

mA = A(i);

mw1 = p(i);

end end

Придадим наглядность изменений резонансной частоты контура и фактического значения через координаты вектора «ухода» [x y] резонансной частоты ω 0 и перпендикуляра [x1 y1] к шкале измерения этой частоты.

x0 = linspace(w0, mw1,50);

y0 = linspace(0, sqrt(mA),50);

x1 = [mw1, mw1];

y1 = [sqrt(mA),0];

Выведем полученные результаты на график (рис. 3):

hold on

F = plot(p, sqrt(A),’LineWidth’,1);

plot(x0, y0,’—’)

plot(x1, y1,’—’)

axis([0.85*w0 1.15*w0 0 1.1*sqrt(mA)])

ylabel(‘A, Кл’,’Rotation’,0);

xlabel(‘p, Рад/сек’,’Rotation’,0);

hold off

Анализ АЧХ колебательного контура с учётом коэффициента нелинейности показал (рис. 3):

• 1.    Знак перед коэффициентом нелинейности определяет сторону «наклона» АЧХ (рис. 4).

• 2.    Увеличение коэффициента нелинейности приводит к «развалу» остроты вершины АЧХ и возникновению области неоднозначности амплитуды и изменению резонансной частоты колебательного контура (рис. 5).

• 3.    Увеличение амплитуды входного напряжения приводит к увеличению влияния коэффициента нелинейности характеристики выходного сигнала, при неизменности этого параметра (рис. 6).

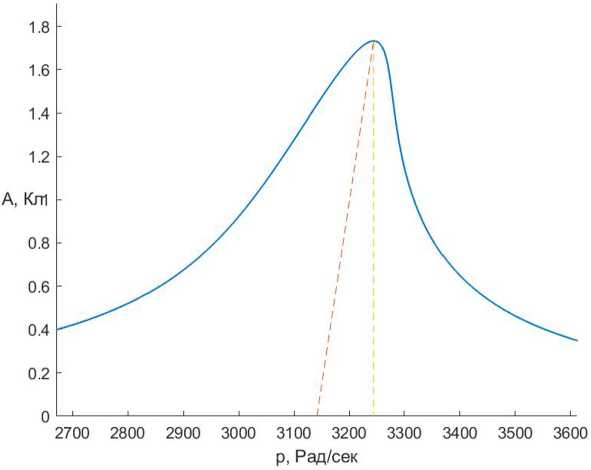
Рис. 3. АЧХ колебательного контура с учетом нелинейности

• Fig. 3.    Amplitude-frequency response of the oscillatory circuit taking into account the nonlinearity

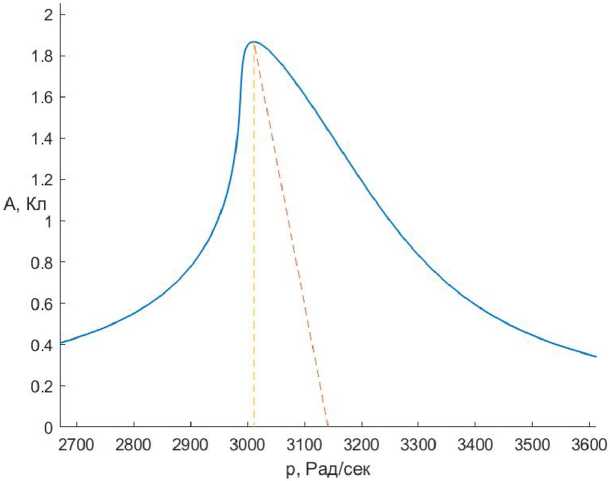
Рис. 4. АЧХ колебательного контура при отрицательном значении коэффициента нелинейности

• Fig. 4.    Amplitude-frequency response of the oscillatory circuit with a negative value of the nonlinearity coefficient

  

  2700 2800 2900 3000 3100 3200 3300 3400 3500 3600

  р, Рад/сек

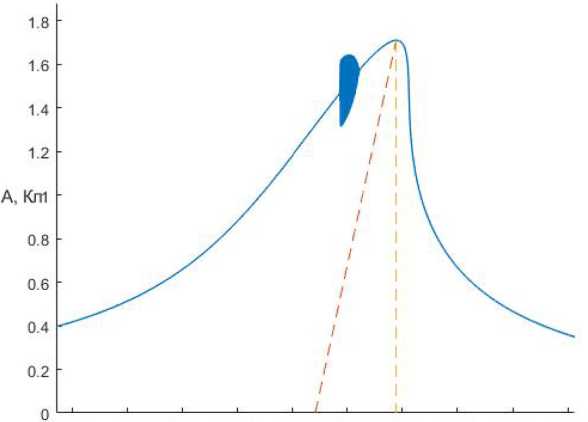
  Рис. 5. АЧХ колебательного контура при увеличении значения коэффициента нелинейности

  
  

  Fig. 5. Amplitude-frequency response of the oscillatory circuit increasing the value of the nonlinearity coefficient

  
  
  

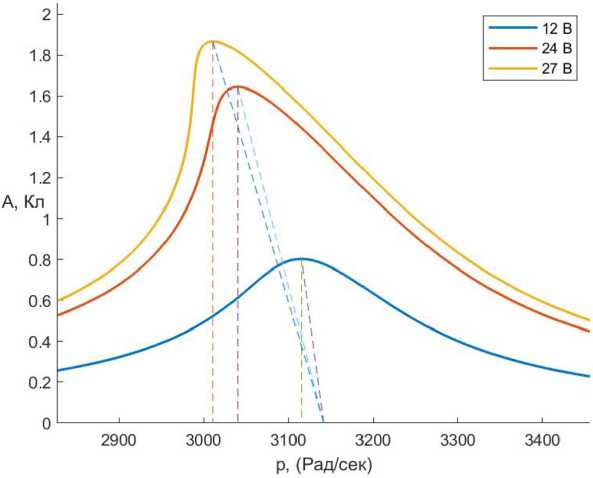
  Рис. 6. АЧХ колебательного контура при разных значениях напряжения входного сигнала

  
  

  Fig. 6. Amplitude-frequency response of the oscillating circuit at different input voltage values

  
  

В дополнении из [1] необходимо отметить, что:

• 1.    Резонанс силового происхождения представляет собой частный случай вынужденных колебаний устойчивой системы, а параметрический резонанс – это проявление неустойчивости равновесного состояния, в силу чего система при строго нулевых начальных условиях остается в положении равновесия и только неизбежные отклонения от этого положения могут привести к раскачке.

• 2.    Параметрический резонанс имеет место не только при некоторых дискретных значениях критических частот, но охватывает целую область неустойчивых состояний в окрестности этих частот.

• 3.    Если при силовом резонансе введение линейной силы сопротивления приводит к ограничению резонансной амплитуды, то параметрический резонанс может привести к неограниченной раскачке и при наличии сопротивления, и лишь превышение определенного уровня диссипации устраняет эту опасность.

• 4.    При параметрическом резонансе амплитуды колебаний нарастают по экспоненциальному закону и обычно очень быстро достигают аварийных значений.

Заключение

Для учёта влияния нелинейности в компонентах с реактивным сопротивлением необходимо использование высококачественных элементов цепи (с наименьшими допусками) и применение фильтров, стабилизирующих амплитуду и частоту колебаний. Также стоит в дальнейшем рассмотреть применение второго типа внешнего воздействия на колебательный контур LC для генерации колебаний – параметрический резонанс. Данный тип внешнего воздействия по ранее проведённым исследованиям исключает неоднозначности в значении амплитуды колебаний, даже при учёте коэффициента нелинейности, лишь ограничивая её максимум.