Анализ влияния модельных условий на оценку геоморфометрических свойств картируемых поверхностей

Задача картирования свойств геологических объектов по ограниченному набору наблюденных значений по своей природе является неоднозначной. Этим обусловлено наличие большого числа методов картирования, а также множества управляющих параметров, влияющих на результаты реализации этих методов. Каждый из этих методов явно или неявно использует некоторые модельные условия, определяющие пространственные закономерности изменения картируемых показателей. При этом достоверность (или недостоверность) конечных результатов картирования, очевидно, определяется согласованностью (или несогласованностью) используемых модельных условий и реальных.

В используемом нами вариационно-сеточном методе геокартирования, реализующем аппроксимационный подход на основе бикубических сплайнов [1-3 и др.], модельные условия задаются в виде системы дифференциальных уравнений в частных производных, достаточно общего вида, до второго порядка включительно. Этим определяется возможность реализации широкого спектра модельных условий, но, вместе с тем и обусловлена необходимость решения задачи по обоснованию выбора конкретных условий, наилучшим образом отвечающим имеющимся фактическим данным.

Поскольку искомые условия представляют собой линейные уравнения, связывающие между собой значения картируемой функции и частные производные первого и второго порядков, то в качестве начального элемента решения этой задачи, очевидно, необходимо достаточно точно определить эти свойства в наборе опорных точек (точек с фактическими данными). Сложность состоит в том, что результаты картирования и, соответственно, значения геоморфометрических параметров могут существенно зависеть от выбранных модельных условий.

В данной работе для оценки влияния такого выбора проводится сопоставительная оценка получаемых значений этих параметров при реализации двух наиболее используемых на практике модельных условий - минимума кривизны и минимума поверхности. Математическая постановка решения задачи в рамках вариационно-сеточного метода геокартирования заключается в нахождении функции двух переменных S(x,y) , обеспечивающей минимум функционала, представляющего собой сумму невязок квадратов отклонений от наблюдаемых значений в заданных точках (x , , у) и интегральных стабилизаторов. При этом искомая функция ищется в классе бикубических сплайнов на равномерной сетке.

Для модельных условий минимума кривизны функционал имеет вид:

»кр = Ркр ^(^(ХрУ,) " Zi)2 + / (s« + 2S^ + ^^ ^' t n для условий минимума поверхности:

^фпв = Рпв ^ (^(^рУ;) - Zj)² + j(⁵x + ^Sy) ^{dx d}y

*                                  £1

Здесь - и

Икр “ ПБ

- весовые коэффициенты с

помощью которых можно контролировать (в определенной степени) точность аппроксимации.

а)

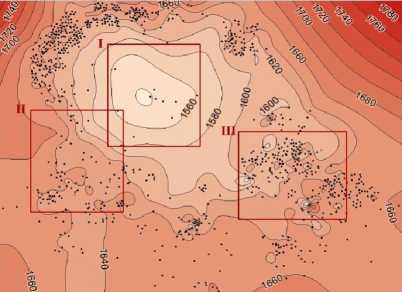
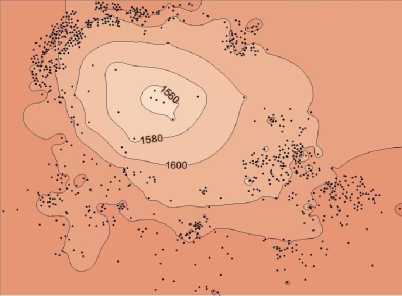
Рис. 1. Картирование по сетке 210 х 161 узлов (а – минимум кривизны, б – минимум поверхности).

б)

Исходными данными для построений выбраны значения отметок кровли пласта в 856 скважинах одного из хорошо изученного месторождения Западной Сибири. Абсолютные отметки изменяются в диапазоне от 1538,5 м до 1668,9 м, среднее значение равно 1630,3 м, стандартное отклонение составляет 17,8 м.

Большой объем используемых фактических значений обеспечивает возможность вариации в широких пределах параметров построения, которые влияют на точность аппроксимации самих показателей, а также на оценки частных производных картируемых поверхностей в точках с данными. Вместе с тем, существенная неравномерность в распределении данных по площади позволяет сопоставить результаты построений в зонах с повышенной и пониженной плотностью исходной информации.

Построения выполнены для двух вариантов детальности используемой сетки сплайнов – 210 узлов по оси Х, 161 узел по оси Y (рис. 1), и 55 узлов по оси Х, 43 узла по оси Y (рис. 2). Для расчетов использован программный комплекс GST1, обеспечивающий широкие возможности по управлению модельными условиями при картопостроении и по использованию комплексных технологий решения задач, связанных с геокартированием [4]. На рис 1а римскими цифрами I, II и III отмечены участки оди- наковой площади с низкой, средней и высокой плотностью расположения данных, для которых далее проведено отдельное сопоставление результатов оценки геоморфометрических показателей.

Весовые коэффициенты Ркр и Рпв подобраны таким образом, чтобы точность аппроксимации была близкой для обоих вариантов используемых модельных условий. Среднеквадратичное отклонение фактических и расчетных значений для приведенных построений при использовании детальной сетки составляет около 1,43 м и около 4,3 м – в варианте с более редкой сеткой. Заметим, что попытки уменьшить ошибки аппроксимации во втором варианте за счет повышения значений весовых коэффициентов Ркр и РпЕ не дают желаемого результата, но наоборот приводят к появлению артефактов, проявляющихся в резких и амплитудных изменениях построенных поверхностей.

а)

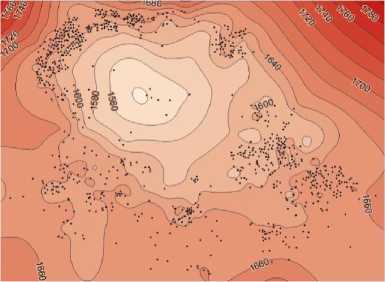
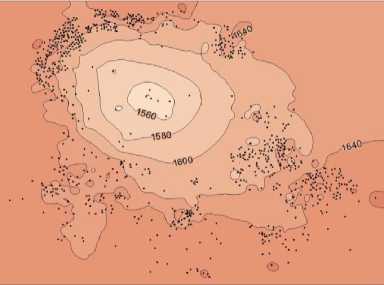
Рис. 2. Картирование по сетке 55 х 43 узлов (а – минимум кривизны, б – минимум поверхности).

б)

Приведенные результаты свидетельствуют о том, что в целом общая картина для всех вариантов расчета во многом схожая – четко прослеживается структурное поднятие слегка вытянутое в северозападном направлении. Вместе с тем при картировании с модельным условием минимума кривизны отличительной чертой является наличие трендовых тенденций к погружению структурного плана в областях экстраполяции (с отсутствием данных). Для каждой из построенных карт в точках расположения фактических данных (xi, yi) вычислены значения погрешностей аппроксимации глубины кровли пласта AS = S(x.Jyl) z., а также значения первых и вторых производных ^х» ^y»^xxi ^w ^ ^ . Использование бикубических сплайнов для представления аппроксимирующей функции позволяет определять эти параметры точно. На этой основе выполнено взаимное сравнение этих параметров, полученных при использовании различных модельных условий. Графическое сопоставление полученных результатов для варианта расчета по детальной сетке (210 х 161 узлов) представлено на рис. 3. Здесь по оси абсцисс отложены значения параметров в модели с минимизацией кривизны (ΔS кр, Sx кр и т.д.), по оси ординат – по модели с минимизацией поверхности (ΔS пв, Sx пв и т.д.).

Как видно из приведенных рисунков, несмотря на существенную разницу в используемых модельных условиях между геоморфометрическими показателями наблюдается хорошая согласованность. Коэффициенты корреляции между ними очень высокие (табл. 1). В заголовках этой и последующих таблиц для коэффициента корреляции ( R ) для краткости используются обозначения Δ S , S_x и т.д. вместо Д(Л5 кр,А5 пв),7?(5х кр,5х пв) и т.д.

выявленная согласованность отражает взаимосвязь не только в окрестности средних значений параметров, но для всей области их изменения.

а)

б)

Таблица 1

Коэффициенты корреляции между геоморфометрическими показателями

Сетка	Δ S	S x	S y	S xx	S уу	S xy
210 х 161(а)	0,96	0,93	0,87	0,90	0,90	0,81
210 х 161(б)	0,95	0,98	0,92	0,90	0,89	0,82
55 х 43	0,99	0,94	0,95	0,94	0,95	0,92

в)

В этой таблице приведены два варианта расчетов по плотной сетке – при среднеквадратичной ошибке аппроксимации 1,43 м (вариант «а»), и при более точной аппроксимации, со среднеквадратичной ошибкой 0,065 м (вариант «б»). Для рассмотренных вариантов коэффициенты корреляции варьируют от 0,81 до 0,98. При уменьшении детальности сетки показатели корреляции увеличиваются и варьируют от 0,92 до 0,99. Это связано с тем, что в этом случае в результате аппроксимации того же объема фактических данных в большей мере проявляются общие трендовые закономерности при картировании.

Характерной чертой выявленных взаимосвязей, помимо высоких значений коэффициентов корреляции, является то, что в точках с большими (по абсолютной величине) ошибками аппроксимации и значениями других параметров сохраняется согласованность (с отдельными исключениями) в их оценках при использовании рассматриваемых модельных условий. Это свидетельствует о том, что г)

д)

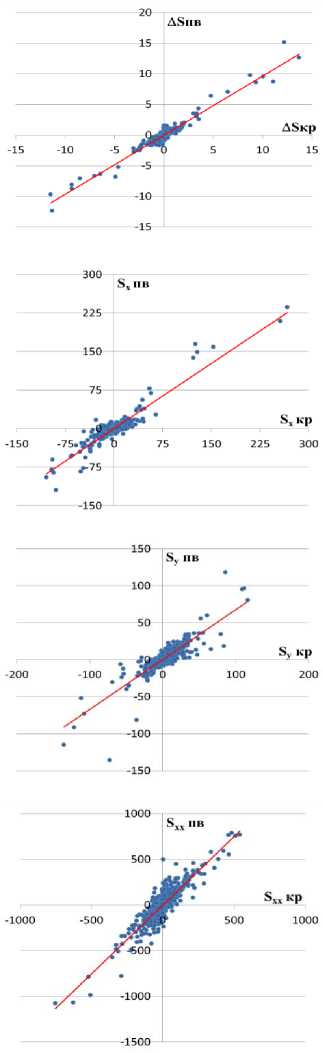
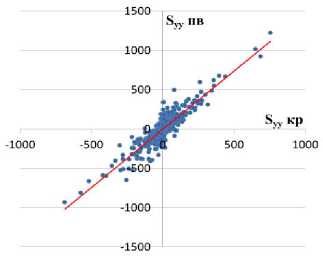
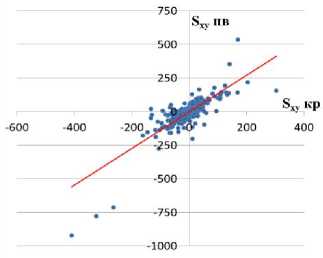
Рис. 3. Сопоставление геоморфометрических свойств

е)

при реализации различных модельных условий (а

–   ; б –5; в –5; г –5; д –5  , е –    ) (а – x      у ^xx -'yy погрешности аппроксимации, б – производные по x, в – производные по y, г – вторые производные по x, д – вторые производные по y, е – смешанные производные).

Приведенные выше результаты сопоставления определения геоморфометрических показателей получены при построении карт в задаче с большим объемом фактических данных, в пространственном распределении которых прослеживается явная неоднородность. И, соответственно, полученные оценки характеризуют некоторые осредненные соотношения для всего набора данных для всей области картирования.

В зонах с различной плотностью расположения фактических данных естественно ожидать отклонения от осредненных закономерностей. Для выполнения такого сопоставления были выбраны три зоны одинаковой площади (рис. 1). В зоне I расположено 11 точек, в зоне II – 79 и в зоне III – 190. В таблице 2 приведены результаты оценок корреляционных соотношений для рассматриваемых гео-морфометрических показателей в этих точках (полученных при картировании по плотной сетке 210х161 узлов для двух вариантов модельных условий – минимума кривизны и минимума поверхности, для варианта «а» со среднеквадратичной ошибкой аппроксимации 1,43 м).

Корреляционные связи характеризуются меньшими значениями в зоне I с небольшим количеством фактических данных (по сравнению с показателями для всех 856 точек, приведенными в таблице 1), а в зоне III с повышенной плотностью данных чуть выше средних значений по всем точкам. Это обусловлено тем, что в области с низкой плотностью данных значения геоморфометрических показателей в большей степени определяются используемыми модельными условиями. Отметим, что точность аппроксимации в зоне с низкой плотностью данных высокая и составляет 0,033 м.

Таблица 2

Коэффициенты корреляции в областях с различной плотностью данных

Область	Δ S	S x	S y	S xx	S уу	S xy
I	0,56	0,47	0,66	0,47	0,52	0,45
II	0,84	0,78	0,75	0,90	0,86	0,83
III	0,98	0,96	0,87	0,94	0,94	0,80

При раздельном построении только по данным в пределах выбранных зон, но с обеспечением общего уровня среднеквадратичной погрешности, сопоставимого с построением по всей области картирования (1,43 м) также сохраняются высокие корреляционные связи между геоморфометрическими показателями для двух вариантов использования модельных условий (табл. 3). При этом в зоне с низкой плотностью данных коэффициенты корреляции слегка увеличиваются, а в зонах с повышенной плотностью практически сохраняются на прежнем уровне.

Таблица 3

Коэффициенты корреляции в областях с различной плотностью данных при раздельном построении

Область	Δ S	S x	S y	S xx	S уу	S xy
I	0,57	0,72	0,74	0,72	0,76	0,35
II	0,79	0,69	0,76	0,89	0,84	0,57
III	0,97	0,97	0,91	0,92	0,94	0,86

Таким образом, представленные в данной работе результаты свидетельствуют о том, что независимо от точности аппроксимации и от плотности сетки узлов сплайна, и, несмотря на использование двух существенно различающихся модельных условий – минимума кривизны и минимума поверхности, в оценках геоморфометрических показателей прослеживается очень высокая согласованность. Этим определяется возможность определения исходных параметров для решения задачи поиска модельных условий, наилучшим образом соответствующим имеющимся фактическим данным, и, в конечном итоге, для повышения прогностических свойств результатов картопостроения.