Анализ влияния настроечных параметров прошивного стана на изменение диаметра и толщины стенки гильзы

Автор: Выдрин Александр Владимирович, Нерозников Владимир Леонидович, Звонарев Дмитрий Юрьевич, Трубников Кирилл Вячеславович

Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy

Рубрика: Обработка металлов давлением. Технологии и машины обработки давлением

Статья в выпуске: 1 т.22, 2022 года.

Бесплатный доступ

В производстве бесшовных труб массовым способом является применение прошивки заготовки на станах винтовой прокатки с последующей раскаткой на станах продольной прокатки. При этом к качеству и геометрическим параметрам готовых труб предъявляют повышенные требования. К геометрическим параметрам относят такие, как толщина стенки, диаметр, разнотолщинность. При этом на разнотолщинность в основном влияет качество гильзы. Известно, что одни и те же геометрические параметры гильзы (диаметр и толщина стенки) возможно получить при различном соотношении настроечных параметров, таких как расстояние между валками, расстояние между удерживающим инструментом, выдвижение оправки за пережим. Однако в этом случае разнотолщинность гильз будет различной. Кроме настроечных параметров на разнотолщинность влияет и степень износа инструмента, в частности оправка прошивного стана. Установлено, что по мере износа оправки прошивного стана диаметр гильзы монотонно увеличивается, что приводит к перераспределению толщины стенки гильзы, а соответственно и разнотолщинности гильзы. Поиску рациональных настроечных параметров с целью минимизации разнотолщинности и посвящена данная работа. Разработан план эксперимента с применением моделирования в среде QForm. Произведена обработка полученных гильз по геометрическим параметрам. На основе данных проведено вычисление коэффициента среднеквадратичной ошибки (RSME) для различных моделей регрессионных уравнений. Для выбранной модели построены номограммы распределения разнотолщинности, толщины стенки, диаметра гильзы в зависимости от настроечных параметров. Данные номограммы могут быть использованы в производственной практике для оперативного вычисления геометрических параметров гильз при изменении условий прошивки заготовок. В качестве примера были разработаны рекомендации для получения гильз с толщиной стенки 17 мм с минимальной разнотолщинностью.

Еще

Компьютерное моделирование, прошивка, настроечные параметры, точность, регрессионные уравнения

Короткий адрес: https://sciup.org/147236549

IDR: 147236549 | DOI: 10.14529/met220105

Текст научной статьи Анализ влияния настроечных параметров прошивного стана на изменение диаметра и толщины стенки гильзы

Для выпуска конкурентоспособной продукции необходимо использовать наилучшие доступные технологии и внедрять современные разработки в производственный процесс. Одними из главных показателей качества готовых труб являются их геометрические параметры, закладываемые еще на стадии первой деформирующей операции – прошивки. Именно от точности гильзы зависят все последующие показатели по толщине стенки и диаметру готовой трубы [1].

Немаловажным параметром в точности труб и гильз является разнотолщинность.

Основным видом разнотолщинности прошиваемых в двухвалковом прошивном стане гильз является эксцентричная поперечная раз- нотолщинность. Этот вывод подтверждают исследования, выполненные с помощью регрессионного анализа [2, 3]. При этом отдельно оценивают величину концевой разнотолщин-ности и разнотолщинность в основной части гильзы. На концевую разнотолщинность влияют такие параметры, как обжатие перед носком оправки, коэффициент овализации, отклонение от перпендикулярности торца заготовки, точность выставления оси прошивки, равномерность нагрева заготовки. Разнотол-щинность средней части зависит от коэффициента овализации, калибровки инструмента, угла подачи, степени износа инструмента, точности выставления оси прошивки и равномерности нагрева заготовки.

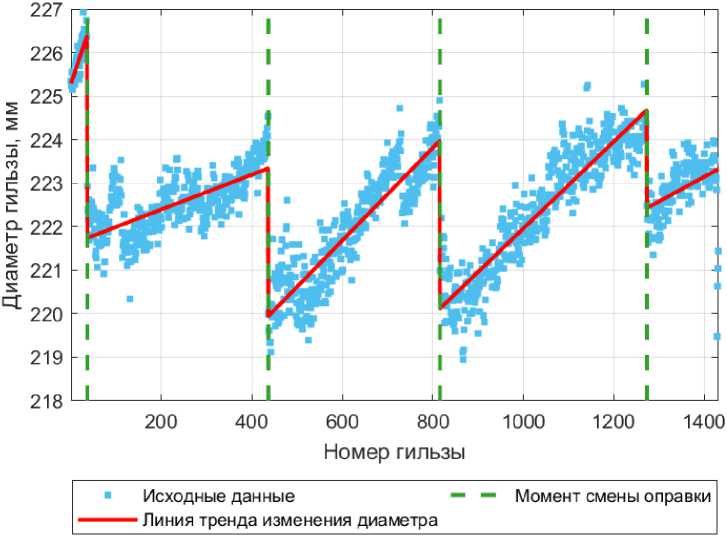
Рис. 1. Изменение диаметра гильзы по мере износа оправки прошивного стана Fig.1. Changing the diameter of the sleeve as the mandrel of the piercing mill wears out

При реа ли за ц и и п роцес са п рош и в к и загото во к пр и раз л ич н ы х на ст р оеч ных парам етрах возможно п ол учи ть од и н а к ов ые зн а че н и я как п о т ол щин е стенки , т ак и по диа м ет р у гильзы [4 ] . Од н ак о в э том с лу ча е ра зн отол-щи нн ость мож е т б ыт ь разли чн а я. К роме э т ого, по мере изно са оп равк и п ро ш и в н ого с та на меняе тся и д и а м е тр ги л ьзы ( ри с. 1) . Д ля оценки с те п е н и в ли ян и я изн ос а н а д и а м е тр ги льз ы были п роа на ли зи ров а н ы д а н н ые , п олу че н н ы е с использованием QAS си ст ем ы , у с та н ов ленн ой н а проши вн ом с та н е А О «Т АГ МЕТ » KSW 1150 VD (см. рис. 1). П редс та в ле н н ая вы бо р ка со о т вет ст вует с у т о ч ному о бъ ем у пр оизводства. З а э то в ре мя в ра б оте н а хо д и лось 4 о пр ав ки. К ак ви дно из рис. 1 п о м ере из н оса оправк и ди а м е тр ги ль зы мон отон н о п овышается.

Это в ча с тн ос ти при в од ит к тому , что п ри неизменных условиях п о вели чи н е обжатий межд у в а лк а ми , в ели чи н а об ж а ти я за готовки п ере д н о с к ом оп ра в к и пос тоян н о у в еличиваетс я и те м с а мым п ов ыш а е тс я ра зн отолщин-ность гильз.

Так и м об ра зом, п ои ск п уте й у ме н ьш е н и я р а з н отол щ и н ности гил ьз за с чет п одб ора настроечных параметров я в л я етс я п е рс п е к тивной задачей.

С целью определения влияния настроечных параметров на величину разнотолщинно- сти гильз был выбран полно факторный эксперимент (ПФЭ) для процесса прошивки заготовки диаметром 210 мм. Известны работы, в которых для определения геометрических размеров гильзы применяются программные продукты, реализующие метод конечных элементов [5], например QForm.

В качестве управляющих параметров были выбраны следующие факторы:

– выдвижение оправки за пережим с пределами изменения значения от 10 до 100 мм с шагом 30 мм;

– расстояние между валками с пределами изменения значения от 170 до 190 мм с шагом 5 мм;

– расстояние между дисками Дишера с пределами значения от 200 до 210 мм.

В результате ПФЭ был реализован со схемой 41 • 51 • 21 = 40 экспериментов. В табл. 1 представлены значения управляющих параметров для каждого варианта моделирования, а также относительные характеристики процесса (обжатие перед носком оправки, обжатие в пережиме, коэффициент овализации).

В качестве выходных параметров фиксировались диаметр гильзы по длине и толщина стенки гильз. Методика оценки толщины стенки и диаметра оценивалась с использованием специализированного программного продукта [5, 6].

Таблица 1

Значения настроечных параметров при моделировании процесса прошивки

Values of setting parameters when simulating the firmware process

Разнотолщинность гильз вычислялась как величина однократного относительного отклонения от математического ожидания средней толщины стенки.

Значения относительного отклонения вычислялись по уравнению

5 = ^ср •ioo %, (1)

^ ср

где S i - текущее значение толщины стенки;

5 _ср - среднее значение толщины стенки.

Доверительный интервал по разнотол-щинности рассчитывался как однократное отклонение от математического ожидания. В качестве примера на рис. 2 представлены гистограммы распределения разнотолщинно-сти для различных настроечных параметров.

Table 1

№ эксперимента	Расстояние между валками, мм	Обжатие в пережиме, %	Выдвижение оправки за пережим, мм	Обжатие перед носком оправки, %	Расстояние между дисками, мм	Коэффициент овализации
1	170	20,2	10	19,6	200	1,18
2					210	1,24
3	175	17,9		17,3	200	1,14
4					210	1,20
5	180	15,6		14,9	200	1,11
6					210	1,17
7	185	13,2		12,6	200	1,08
8					210	1,14
9	190	10,9		10,2	200	1,05
10					210	1,11
11	170	20,2	40	17,6	200	1,18
12					210	1,24
13	175	17,9		15,3	200	1,14
14					210	1,20
15	180	15,6		12,9	200	1,11
16					210	1,17
17	185	13,2		10,6	200	1,08
18					210	1,14
19	190	10,9		8,2	200	1,05
20					210	1,11
21	170	20,2	70	15,6	200	1,18
22					210	1,24
23	175	17,9		13,2	200	1,14
24					210	1,20
25	180	15,6		10,9	200	1,11
26					210	1,17
27	185	13,2		8,5	200	1,08
28					210	1,14
29	190	10,9		6,2	200	1,05
30					210	1,11
31	170	20,2	100	13,5	200	1,18
32					210	1,24
33	175	17,9		11,1	200	1,14
34					210	1,20
35	180	15,6		8,8	200	1,11
36					210	1,17
37	185	13,2		6,5	200	1,08
38					210	1,14
39	190	10,9		4,1	200	1,05
40					210	1,11

В табл. 2 представлены сводные результаты по определению геометрических параметров гильзы (средняя толщина стенки, раз-нотолщинность) согласно проведенному ПФЭ. Стоит отметить, что полученные результаты

схожи с результатами замеров гильз автоматической системой QAS.

Используя программный продукт MATLAB, провели определение регрессионной модели. Результаты вычисленной среднеквадратичной

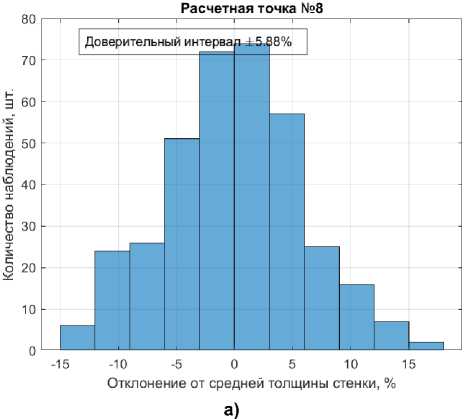
Рис. 2. Распределение разнотолщинности гильз при реализации настроечных параметров

Fig. 2. Distribution of case thickness differences in the implementation of tuning parameters

Таблица 2

Результаты вычислений геометрических показателей гильзы

Table 2

The results of calculating the geometric parameters of the sleeve

№ эксперимента	Средняя толщина стенки, мм	Разнотолщинность, ±%	Средний диаметр гильзы, мм
1	16,81	6,99	225,90
2	17,03	8,53	231,10
3	19,01	5,87	227,06
4	19,21	6,35	231,25
5	21,28	4,69	228,29
6	21,28	5,53	231,42
7	23,71	4,06	229,09
8	24,14	5,88	236,13
9	25,05	4,89	230,60
10	24,98	5,32	234,35
11	15,83	10,33	224,05
12	15,42	8,84	226,48
13	18,25	9,8	226,26
14	17,63	7,31	227,23
15	20,14	7,09	225,51
16	20,03	6,41	228,15
17	22,37	5,75	225,26
18	22,24	5,17	228,61
19	25,11	6,71	229,72
20	24,04	4,93	229,73
21	13,85	12,99	219,22
22	14,21	13,05	223,51
23	16,49	10,6	222,72
24	16,41	10,62	224,42
25	18,48	8,60	221,14

Окончание табл. 2

Table 2 (end)

№ эксперимента	Средняя толщина стенки, мм	Разнотолщинность, ±%	Средний диаметр гильзы, мм
26	18,75	8,78	225,35
27	20,82	5,19	221,10
28	21,07	6,54	225,46
29	22,86	5,64	224,26
30	23,08	4,78	225,35
31	14,49	12,25	219,90
32	14,71	12,49	222,57
33	16,03	10,93	220,41
34	16,25	11,28	223,09
35	17,87	9,16	220,81
36	18,14	9,66	223,82
37	19,74	7,52	221,53
38	20,09	8,11	224,71
39	21,40	6,68	222,97
40	21,85	7,16	226,15

Таблица 3

Сводные данные результатов обучения регрессионных моделей

Table 3

Summary of learning outcomes for regression models

Название модели Средняя толщина стенки, мм Разнотолщинность, ±% Средний диаметр гильзы, мм RSME R2 RSME R2 RSME R2 Linear [7] 0,19887 1,0 1,0153 0,84 1,3255 0,88 Interaction Linear [8] 0,19284 1,0 0,87169 0,88 1,32 0,88 Robust Linear 0,2 1,0 1,0176 0,84 1,363 0,87 Stepwise Linear 0,19887 1,0 0,87222 0,88 1,3255 0,88 Fine Tree [9] 1,2115 0,85 1,1348 0,8 2,3459 0,61 Medium Tree 3,0852 0 1,7287 0,53 3,7604 0 Coarse Tree 3,0852 0 2,5181 0 3,7604 0 Linear SVM [10] 0,39293 0,98 1,0322 0,83 1,4674 0,85 Quadratic SVM [11] 0,26311 0,99 0,82607 0,89 1,4409 0,85 Cubic SVM [12] 0,25852 0,99 0,60205 0,94 0,91528 0,94 Fine Gaussian SVM 0,75696 0,94 0,63013 0,94 1,9462 0,73 Medium Gaussian SVM 0,55338 0,97 0,51642 0,96 1,5979 0,82 Coarse Gaussian SVM 1,099 0,87 1,1413 0,79 2,6737 0,49 Boosted Trees [13] 1,486 0,77 0,78735 0,9 9,7834 0 Bagged Trees [14] 2,6337 0,27 1,7868 0,5 2,831 0,43 Squared Exponential GPR [15] 0,19332 1,0 0,25041 0,99 1,3042 0,88 Matern 5/2 GPR [16] 0,1933 1,0 0,19029 0,99 1,287 0,88 Exponential GPR 0,000487 1,0 0,00058 1,0 0,00071666 1,0 Rational Quadratic GPR 0,19332 1,0 0,21967 0,99 1,3042 0,88 Narrow Neural Network [17] 0,16747 1,0 0,71008 0,92 1,2241 0,89 Medium Neural Network 0,13575 1,0 0,35264 0,98 0,73677 0,96 Wide Neural Network [18] 0,13553 1,0 0,00098681 1,0 0,72444 0,96 Bilayered Neural Network 0,13553 1,0 0,17054 1,0 1,1166 0,91 Trilayered Neural Network 0,074267 1,0 0,31852 0,98 0,62814 0,97 ошибки (RSME) и коэффициента детермина-циим (R2) для различных моделей представлены в табл. 3.

Как видно из табл. 3, для оценки разно- толщинности наибольшая точность была получена в модели Exponential GPR (рис. 3а) по сравнению с другими моделями (рис. 3b).

На основе полученного уравнения были

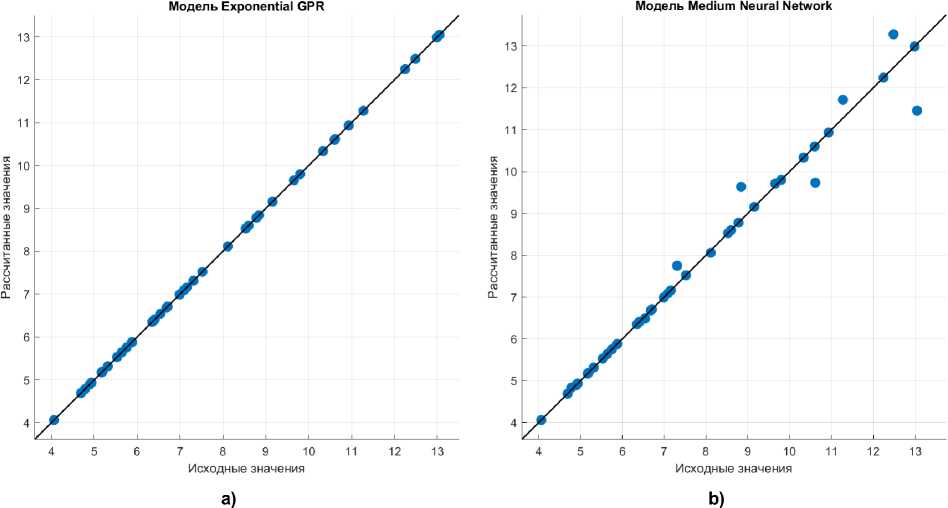
Рис. 3. Распределение отклонений рассчитанных значений разнотолщинности от исходных Fig. 3. Distribution of deviations of the calculated values of thickness variation from the initial ones

построены номограммы р а с п ред е ле н и я разно-т о л щинно ст и (р ис. 4 ), т о лщины ст енки (рис. 5 ) и диаметра гильзы (рис. 6).

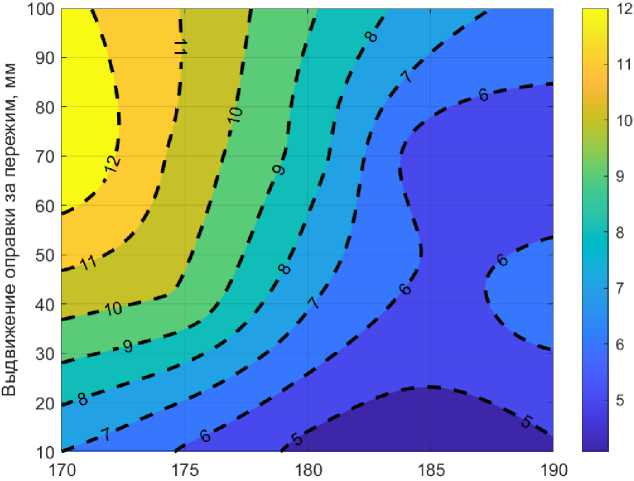
Из представленных рис. 4–6 можно сделать вывод о том, что при выдвижении оправки за пережим, равном 30 мм, расстоянии между валками 180 мм разнотолщинность со- ставит 6,3 % при толщине стенки 20,6 мм, и диаметре 226,6 мм.

Для получения толщины стенки гильзы, равной 17 мм, с наименьшей разнотолщинно-стью необходимы следующие настроечные параметры: расстояние между валками – 171 мм, выдвижение оправки – 10 мм и расстояние

Расстояние между валками, мм

Рис. 4. Распределение разнотолщинности гильзы в зависимости от настроечных параметров

Fig. 4. The distribution of the variation in the thickness of the sleeve depending on the setting parameters

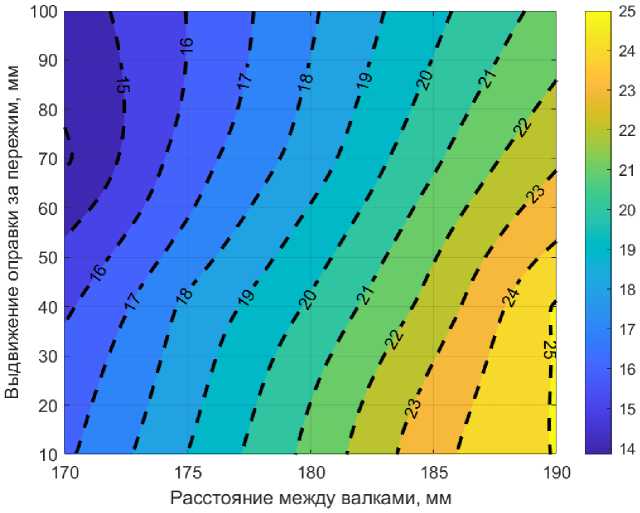
Рис. 5. Распределение толщины стенки гильзы в зависимости от настроечных параметров

Fig. 5. The distribution of the wall thickness of the sleeve depending on the setting parameters

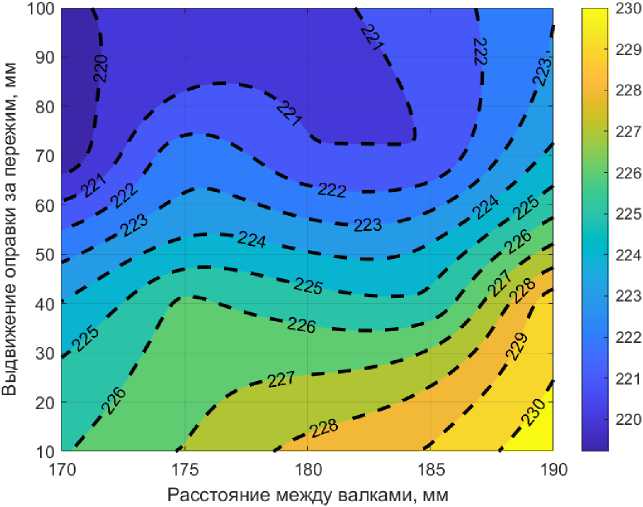
Рис. 6. Распределение диаметра гильзы в зависимости от настроечных параметров

Fig. 6. Sleeve diameter distribution depending on the setting parameters

между дисками Дишера – 2 00 мм . В э том сл у ч а е ра зн отолщи нн ост ь гил ьз с ос та в и т 6, 9 %.

В итоге полученные уравнения возможно использовать для определения рациональных настроечных параметров с целью получения гильз и труб с минимальной разнотолщин- ностью. Кроме этого, показана возможность получения одинаковых геометрических параметров гильзы с использованием номограмм, что в свою очередь позволяет более оперативно проводить корректировки на пульте прошивного стана.

Список литературы Анализ влияния настроечных параметров прошивного стана на изменение диаметра и толщины стенки гильзы

Выдрин А.В., Широков В.В. Теоретические основы повышения точности размеров труб при прокатке на непрерывном стане // Вестник ЮУрГУ. Серия «Металлургия». 2011. № 14 (231). С. 81–86.
Причины разностенности гильз и труб на непрерывном трубопрокатном агрегате ТПА 30-102 и меры их устранения / В.Я. Остренко, И.А. Чекмарев, В.Л. Хмель и др. // Металлургическая и горнорудная промышленность. 1978. № 3. С. 22–24.
Эффективность гармонического анализа для определения точности труб / В.Я. Остренко, И.М. Суконник, А.П. Марголиус и др. // Металлургическая и горнорудная промышленность. 1977. № 1. С. 71–73.
Звонарев Д.Ю., Нерозников В.Л., Выдрин А.В. Определение настроек прошивного стана с помощью цифровых технологий // Черные металлы. 2019. № 9. С. 24–30.
Коликов А.П., Романцев Б.А., Алещенко А.С. Обработка металлов давлением: теория процессов трубного производства. М.: Издат. Дом НИТУ «МИСиС», 2019. 502 с.
Оценка точности формоизменения концов труб при калибровании / Д.А. Ахмеров, Д.Ю. Звонарев, А.В. Выдрин и др. // Вестник ЮУрГУ. Серия «Металлургия». 2020. Т. 20, № 4. С. 39–47. DOI: 10.14529/met200405
Свидетельство о государственной регистрации программы для ЭВМ № 2020662611 Российская Федерация. Программа для расчета геометрических параметров труб при моделировании в среде QForm. № 2020661915; заявл. 08.10.2020; опубл. 16.10.2020 / Д.Ю. Звонарев, М.А. Павлова, Д.А. Ахмеров, М.А. Зинченко; заявитель Открытое акционерное общество «Российский научно-исследовательский институт трубной промышленности» (ОАО «РосНИТИ»).
DuMouchel W.H., O’Brien F.L. Integrating a robust option into a multiple regression computing environment // Computer science and statistics: Proceedings of the 21st symposium on the interface. American Statistical Association, Alexandria, VA, 1989. P. 297–302.
Holland P.W., Welsch R.E. Robust regression using iteratively reweighted least-squares // Communications in Statistics-theory and Methods. 1977. Vol. 6, no. 9. P. 813–827. https://doi.org/10.1080/03610927708827533
Loh W.-Y. Regression tress with unbiased variable selection and interaction detection // Statistica sinica. 2002. Vol. 12, no. 2. P. 361–386.
Waugh S.G. Extending and benchmarking Cascade-Correlation: extensions to the Cascade-Correlation architecture and benchmarking of feed-forward supervised artificial neural networks. PhD thesis. University of Tasmania, 1995.
The population biology of abalone (Haliotis species) in Tasmania. I. Blacklip abalone (H. rubra) from the north coast and islands of bass strait / W.J. Nash, T.L. Sellers, S.R. Talbot et al. Sea Fisheries Division, Technical Report 48, 1994. https://doi.org/10.14264/uql.2016.814
Kecman V., Huang T.-M., Vogt. M. Iterative Single Data Algorithm for Training Kernel Machines from Huge Data Sets: Theory and Performance // Support Vector Machines: Theory and Applications / Edited by Lipo Wang. Berlin: Springer-Verlag, 2005. P. 255–274. https://doi.org/10.1007/10984697_12
Friedman J.H. The elements of statistical learning: Data mining, inference, and prediction. Springer open, 2017.
Friedman J.H. Greedy function approximation: A gradient boosting machine // Annals of statistics. 2001. Vol. 29, iss. 5. P. 1189–1232. DOI: 10.2307/2699986
Nocedal J., Wright S. Numerical optimization. Springer Science & Business Media, 2006.
Convergence properties of the Nelder–Mead simplex method in low dimensions / J.C. Lagarias, J.A. Reeds, M.H. Wright, P.E. Wright // SIAM Journal on optimization. 1998. Vol. 9, no. 1. P. 112–147. https://doi.org/10.1137/s1052623496303470
Glorot X., Bengio Y. Understanding the difficulty of training deep feedforward neural networks // Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR Workshop and Conference Proceedings, 2010. P. 249–256.

Еще

Статья научная