Анализ влияния обратной связи по решению при обработке сигналов в каналах с межсимвольной интерференцией на ограниченном интервале анализа

В рамках данной статьи под межсимвольной интерференцией (МСИ) мы будем понимать нарушение взаимной ортогональности между элементами принимаемой сигнальной последовательности:

( ф ( t ) , ф ( t — k • T ) ) ^ 0; k = ± 1, ± 2, ± 3.. , (1) где Ф ( t ) - вектор-функция элемента принимаемой сигнальной последовательности, (,) – знак скалярного произведения в гильбертовом или евклидовом пространстве.

Основными причинами, вызывающими МСИ, являются многолучевое распространение сигнала в канале связи [1-2] и повышенная удельная скорость модуляции, когда тактовая частота системы превышает удвоенную полосу занимаемых частот (т.н. скорость Найквиста) [3-4].

В настоящее время разработаны разнообразные варианты демодуляторов, предназначенных для работы в каналах с межсимвольной интерференцией.

К таким демодуляторам относятся, например, демодуляторы, в основе которых лежит правило обобщённого максимального правдоподобия [1], которое можно сформулировать следующим образом:

где z ( t ) = s ( t ) + n ( t ) - вектор-функция сигнала на входе демодулятора; n ( t ) - вектор-функ-

I -1

ция аддитивного шума; s ( t ) = ^ ф ( t - i • T ; b i ) - i = 0

вектор-функция поле зной со ставляющей принимаемого сигнала; i е 0 ; I - 1 - номер демодули-руемого сигнального элемента в принимаемой последовательности; I – длина принимаемой последовательности (пакета); T – тактовый интервал; b _i – амплитуда демодулируемого сигнального элемента, которая, в общем случае (при использовании К АМ), п редставляет собой двумерный вектор; m e G;M-1 - один из возможных номеров позиции демодулируемого сигнального элемента; m i - решение относительно номера позиции демодулируемого сигнального элемента; M – позиционность используемой сигнальной системы; B i = b 1 .. b i_ b i _{+ 1} .. b I ^| - вектор амплитуд сопровождающих сигнальных элементов (как предшествующих де модули руемому, так и последующих за ним); k g 1; M I ^{- 1} - номер варианта вектора сопровождающих символов; w ( z ( t ) |b i = b ^{( m )} ; B i = B ^{( k )} ) – условная функция распределения указанного вектора при фиксированных вариантах амплитуды демодулируемого сигнального элемента b i = b ^{( m )} и последовательности сопровождающих символов B i = B ^{( k} ) .

При АБГШ на выходе канала связи решающее правило (2) сводится к сравнению гильбертовых метрик, вычисляемых на некотором интервале анализа T _A с учётом действия всех сигнальных составляющих:

zs bi =argmin⎨ m

min ⎨

J2 ^ J ( Z j ( t ) -S j ( t ; b ( ^{m )} , B < ^k > ) )

j=1 T

dt⎬⎬

m i = arg max m

{max {w (z (t )| b

= b ^{( m )} ; B _y = B ^{( k} ) ) } } (2)

= arg min ^ min <| z ( t ) - s ( t ; b ^{( m )} , B ^{( k} )

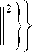
где s ( t ; b ^{( m )} , B ^{( k} ) ) - вектор-функция опорного сигнала, j – номер сигнальной составляющей (на-

пример, одного из сигналов на выходе квадратурного расщепителя, подключённого к соответствующей ветви разнесения), J – общее число таких составляющих.

В общем случае интервал анализа T _A определяется длительностью всего сигнального пакета

с учётом временного рассеяния в канале связи. Такой метод можно определить как «приём в целом всего сигнального пакета с принятием решения о конкретном символе с номером i ».

Очевидно, что такой подход представляет чисто теоретический интерес, поскольку в процессе демодуляции в соответствии с алгоритмом (3) приёмное устройство может принять решение о всей принимаемой последовательности в соответствии с правилом максимального правдоподобия.

Отметим также, что при существенной длине сигнального пакета реализация алгоритма (3) наталкивается на непреодолимые трудности. В ряде публикаций [1-2] рекомендуется ограничить величину T _A длительностью демодулируемого сигнального элемента, поскольку в данном временном интервале содержится вся энергия демо-дулируемого сигнального элемента:

T a = ( Q + 1 ) • T (4) где Q – относительный интервал временного рассеяния в канале связи (т.н. «память канала») [1,2].

При таком подходе общее число перебираемых альтернатив составляет величину

K = M 2Q + 1 (5)

Из соотношения (5) следует, что при больших M и Q практическое применение алгоритма (3) затруднительно, поскольку его вычислительная сложность возрастает по показательному закону как при увеличении позиционности сигнальной системы, так и при увеличении интервала временного рассеяния единичного элемента принимаемого сигнала.

В этом аспекте особый интерес представляют демодуляторы, синтезированные на основе методов линейной коррекции (линейные выравниватели) [3-6], достоинством которых является относительно невысокая вычислительная сложность, возрастающая по линейному закону при увеличении относительной памяти канала и не зависящая от позиционности сигнальной системы.

Еще в 1965 г. Тафтсом было показано [3], что оптимальная структура выравнивателя применительно к различным критериям оптимизации представляет собой каскадное соединение фильтра, согласованного с единичным элементом принимаемого сигнала (СФ), и выравнивающего фильтра (ВФ), который, как правило, представляет собой трансверсальный фильтр конечной длины, задержка между отводами которого определяется тактовым интервалом T .

Отметим, что в общем случае СФ является многомерным, т.е. включает в себя элементарные фильтры, согласованные с составляющими век-тор-функции единичного элемента принимаемого сигнала.

Сигнал на выходе такого многомерного фильтра (ММСФ) при использовании линейной амплитудной модуляции (ЛАМ) можно представить следующим образом:

I 1

y(t)=z(t)®ф(to -t) = Eb-v(t-i■ T) (6)

i = 1

где у ( t ) = ф ( t ) ® ф ( t ₀ - 1 ) - автокорреляционная функция (АКФ) единичного элемента принимаемого сигнала, t ₀ – задержка, определяемая из условия каузальности.

Отсчёты сигнала с выхода ММСФ, взятые в моменты времени i ' T ⁺ t o подаются на вход линии задержки с 2 • L + 1 отводами, к которым подключены весовые элементы θ _l , выходы которых заведены на общий сумматор [3-4].

Отсчёт на выходе выравнивающего фильтра (ВФ) определяется как скалярное произведение вектора отсчетов принимаемой смеси с выхода ММСФ и вектора весовых элементов:

X = У ' ^х ® = r i + U , (7) где i определяет номер демодулируемого сигналь^ного элемента, y' = [ jy. _ L ₊ i .. jy ₄ y y _M .. ^.₊ L - 1 ] ^{- со}ответствующий вектор отсчётов с выхода ВФ, 0* = [ 6 _ _{L + 1} .. О , , 6 0 6 1 .. 6 _L _ 1 ] - вектор весовых элементов выравнивающего фильтра, r_i – его сигнальная составляющая, u_i – его шумовая составляющая, ' – символ транспонирования.

В геометрическом смысле процедура выравнивания сводится к вычислению проекции принимаемой сигнальной последовательности на направление вектора весовых элементов выравнивающего фильтра, который выбирается в соответствии с некоторым критерием оптимизации.

Наиболее широкое применение нашли выравнивающие фильтры, отводы которых оптимизированы в соответствии с критерием минимума среднеквадратического отклонения (СКО) [3-4].

Применение обратной связипо решению

Для введения обратной связи по решению (ОСР) в алгоритме (3) следует вычесть из вектор-функции принимаемой смеси z ( t ) последействия от сигнальных элементов, предшествующих демодулируемому:

i-Q zocp (t)=z (t) - S ф (t -z • T; bz)      (8)

Z=-1

С учётом (8) алгоритм (3) можно представить следующим образом:

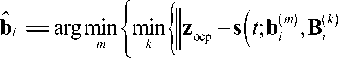
I я

где m e G;M-1; k el; M ^Q .

Алгоритм с учетом допущений и получил название алгоритма приёма в целом с поэлементным принятием решения [1-2] или алгоритма Кловского-Николаева (АКН).

Данный алгоритм хорошо проявил себя при работе в каналах декаметрового диапазона с многолучевым распространением при передаче дискретных сообщений со средними скоростями (1,2 кбит/с – 2,4 кбит/с) при реализации на относительно несложной элементной базе [5].

Из сопоставления соотношений (5) и (9) следует, что при введении ОСР число перебираемых альтернатив многократно сокращается, что сни- жает вычислительную сложность данного алго- ритма.

Выравниватели с обратной связью по решению (decision-feedback equalizers – DFBE) [4-6]

нашли широкое применение в системах передачи дискретных сообщений. В этом случае, как правило, вычитание вектора последействий осуществляется из вектора сигнальной последовательности, записанного в линии задержки ВФ. В этом случае полезная составляющая отсчёта на выходе последнего, обусловленная демодулиру- емым сигнальным элементом, определяется следующим образом:

w _i =

■Q;        ( - )

r — S b - j • ф„ j ®_t ,

^

где r = |^r ( i • T )    r ( ( i -1 ) • T ) .. r ( ( i - L + 1 ) • T ) J

- вектор размера 1 x L , элементами которого являются отсчёты полезной составляющей сигнала на выходе СФ, записанные в линии задержки ВФ, © i - вектор отводов ВФ размера L x 1, ^ ⁽ j - векторы отсчётов сигнальных элементов на выходе СФ, предшествующие демодулируемому.

Характеристики качества

При анализе помехоустойчивости алгоритмов демодуляции были рассмотрены как вероятностные, так и дистанционные характеристики качества.

Вероятностные характеристики были получены методом имитационного моделирования при передаче 8192 сигнальных пакетов, содержащих по 256 элементов каждый. При этом использовалась двоичная система противоположных сигналов, т.е. предполагалось, что M=2. Моделирова-ниеосуществлялось дляслучаяоднойсигнальной компоненты (то есть при J=1).

Единичный элемент принимаемой сигнальной последовательности определялся как супер-позиция сдвинутых во времени элементарных сигналов различной интенсивности (сигналов отдельных лучей):

P

Ф ⁽ t ) = S Y p • g ( t "^T p ) , (11) p=1

где p = 1,2,..P - номер луча, Y p - его амплитуда, ^T p - его задержка относительно сигнала первого луча, g ( t ) определяет форму единичного сигнального элемента на передаче.

Сигнал g ( t ) ограничен по полосе частотой ¹

F =---, его квадрат модуля спектральной плот-

2 • T ности (по Фурье) имеет антисимметричный спад относительно частоты F, что обеспечивает ортогональность передаваемых сигнальных элементов, сдвинутых друг относительно друга на величину, кратную тактовому интервалу T, причём полоса спада составляет величину AF = 0.5 • F .

Отношение сигнал/шум на входе демодулятора определялось как отношение энергии единичного элемента принимаемой сигнальной последовательности E _ϕ к спектральной плотности мощности аддитивной помехи N 0 :

( Q + 1 ) - T

E J ф2 (t) dt h2 = _JL = _o---------       (12)

N 0 N 0

В качестве дистанционных характеристик переборных алгоритмов (3) и (9) использовалась величина

dm- = mmmin {Ib(t; B' ’) -• (t;Bi-'"* )lГ} «з> m≠μ

где Bi^{m , k} ) , B i ^’ ^{к )} _- - полные векторы сигнальных амплитуд, попадающие в интервал анализа:

B imk ⁾ =[ b ikQ    ..    b ikQ    b i^{m )}    b ’ + i    ..    b < : Q] ;

Bi"'K1 = [bi-Q   ..   bi-Q   b'"'   b'K*   ..   bi+Q];

при использовании алгоритма (3) без ОСР, и

B ( ^{m , k} ) =[ b im ) b ( + ) .. b ( + Q ] ;

B ⁽ ^^{K )} =[b ⁽ ^ ) b ⁽ : )    .. b ⁽ + Q ] ;

при использовании алгоритма (9), предполагающего наличие ОСР.

Величина dm2in определяет минимальное расстояние между всеми возможными парами принимаемых сигнальных последовательностей, которые отличаются позициями сигнального элемента с номером i.

Применительно к демодуляторам на основе линейных выравнивателей в качестве дистанционной характеристики используется относитель- ная эквивалентная метрика d2 =----1, eq OxB xO'

где B – нормированная автокорреляционная матрица вектора шумовых отсчётов в линии задержки ВФ.

Данная характеристика определяет энергетический проигрыш демодулятора по сравнению со случаем приёма одиночного сигнального элемента на согласованный фильтр (то есть в отсутствие МСИ).

На рис. 1-2 приведены вероятностные характеристики (зависимости коэффициента ошибок от отношения сигнал/шум) для алгоритма (3) без ОСР, и алгоритма (9) при идеализированной и реальной ОСР для двухлучевого и трёхлучевого каналов соответственно.

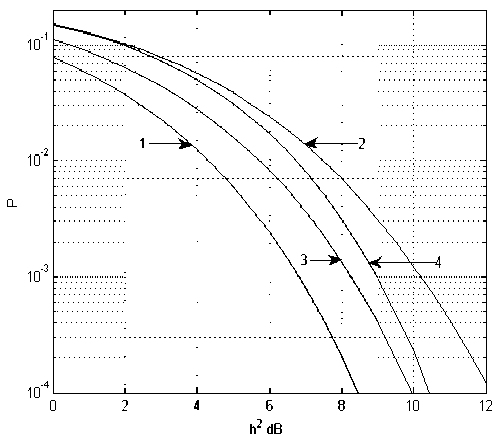
Рис. 1. Характеристики помехоустойчивости при работе в двухлучевом канале связи с фиксированными параметрами (J= 1, LP = 2, Y1 = Y2T-T1 =1.5-T): 1 -приём одиночных сигнальных элементов (отсутствие МСИ); 2 – демодуляция по алгоритму без ОСР (т.е. при полном переборе всех возможных сигнальных последовательностей сигнальных элементов как предшествующих демодулируемому, так и пос- ледующих за ним); 3 – демодуляция в соответствии с алгоритмом Кловского-Николаева (АКН) при идеализированной ОСР; 4 – демодуляция в соответствии с АКН при реальной ОСР.

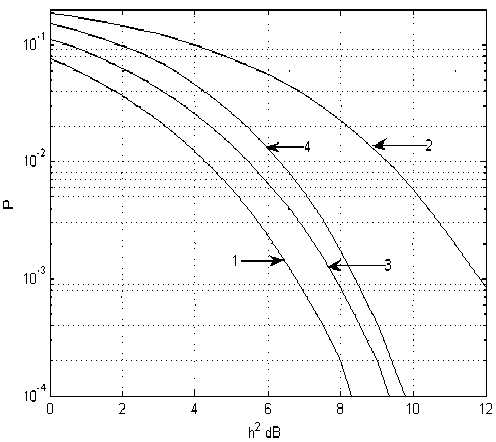
Рис. 2. Характеристики помехоустойчивости при работе в трехлучевом канале связи с фиксированными параметрами ( J = 1, L P = 3, Y 1 = 1, Y 2 =~ 1, Y ₃ = 0,6; т 2 - T 1 = 1,5 • T , t 3 -T 1 = 3,5 • T ): 1 - прием одиночных сигнальных элементов (отсутствие МСИ); 2 – демодуляция по алгоритму (3) без ОСР (то есть при полном переборе всех возможных сигнальных последовательностей сигнальных элементов как предшествующих демодулиру-емому, так и последующих за ним); 3 – демодуляция в соответствии с алгоритмом Кловс-кого-Николаева (АКН) при идеализированной ОСР; 4 – демодуляция в соответствии с АКН при реальной ОСР.

Из анализа результатов, представленных на указанных рисунках, следует, что поэлементная демодуляция последовательностей обеспечивает существенно лучшие результаты при использовании обратной связи по решению (алгоритм (9)) по сравнению с демодуляцией, предусматривающей полный перебор всех возможных сигнальных последовательностей сигнальных элементов как предшествующих демодулируемому, так и последующих за ним (алгоритм (3)).

Отметим, что этот результат получен при интервале анализа, равном интервалу временного рассеяния сигнального элемента в канале связи.

Данный результат подтверждается дистанционными характеристиками,представленными на рис.3.

Представленные на этом рисунке кривые демонстрируют характер изменения величины d ^in , определяемой соотношением (13), при изменении амплитуды второго луча применительно к двухлучевому каналу связи.

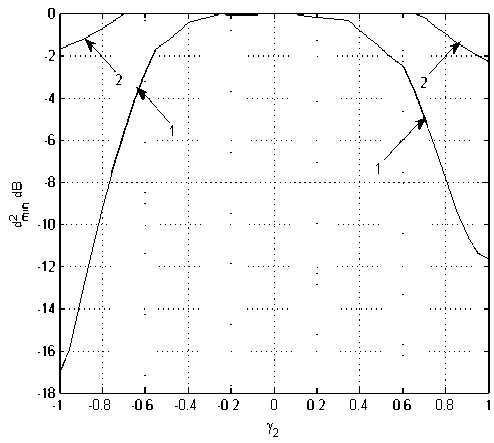
Рис. 3. Зависимость относительной эквивалентной метрики d m2 , определяемой (13), от амплитуды второго луча при демодуляции по алгоритму (3): 1 – в отсутствие ОСР; 2 – при наличии идеализированной ОСР

Как следует из представленного рисунка, величина d _m ² _in при демодуляции с ОСР убывает существенно медленнее, чем при демодуляции, предусматривающей полный перебор на интервале временного рассеяния единичного сигнального элемента в канале связи всех возможных последовательностей сигнальных элементов как предшествующих демодулируемо-му, так и последующих за ним.

Таким образом, из представленных в данном разделе результатов следует, что применение обратной связи по решению существенно улучшает различимость сигнальных последовательностей при использовании алгоритмов переборного типа, в основе которых лежит правило обобщённого максимального правдоподобия.

С другой стороны, сравнение кривых 3 и 4 на рис. 1 и рис. 2 позволяет сделать вывод о том, что эффект размножения ошибок в цепи ОСР существенно влияет на помехоустойчивость таких демодуляторов.

На рис.4 и рис.5 приведены вероятностные характеристики для выравнивателя без ОСР, а также характеристики для выравнивателя с ОСР, как при идеализированной ОСР, так и при реальной ОСР.

Векторы весовых коэффициентов Θ для обоих типов выравнивающих фильтров определялись в соответствии с критерием минимума СКО и изменялись в процессе моделирования в соответствии с отношением сигнал/шум. Моделирование осуществлялось для тех же вариантов канала связи с фиксированными параметрами, что и для демодуляторов переборного типа.

Сравнительный анализ представленных на рис.4 и рис.5 вероятностных характеристик позволяет сделать вывод о том, что использование ОСР на основе методов линейной коррекции также позволяет улучшить помехоустойчивость несмотря на эффект размножения ошибок.

Эти результаты подтверждают соответствующие дистанционные характеристики, представленные на рис. 6, которые были рассчитаны по формуле (14) для отношения сигнал/ шум 7дБ.

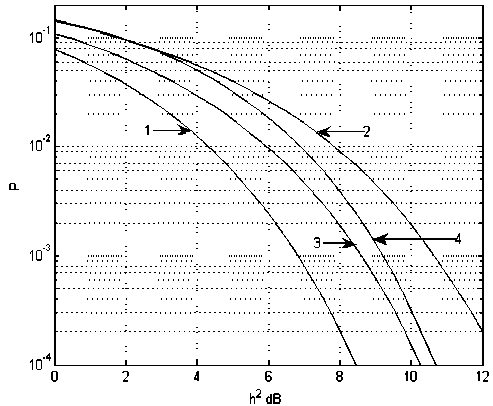
Рис. 4. Характеристики помехоустойчивости при работе в двухлучевом канале связи с фиксированными параметрами ( J = 1, L P = 2, Y 1 = Y 2 , T 2 ~т 1 = 1 ,5- T ): 1 -приём одиночных сигнальных элементов (отсутствие МСИ); 2 – демодуляция с помощью выравнивателя без обратной связи по решению; 3 – демодуляция с помощью выравнивателя при идеализированной ОСР; 4 – демодуляция с помощью выравнивателя при реальной ОСР.

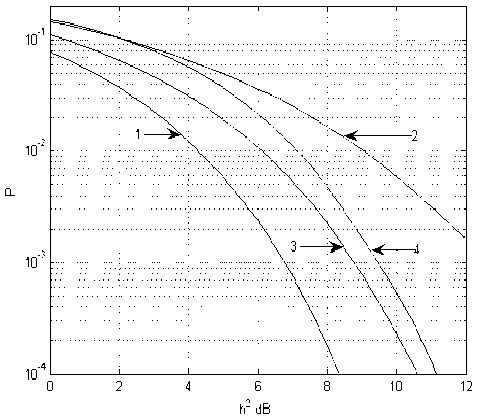
Рис. 5.Характеристики помехоустойчивости при работе в трёхлучевом канале связи с фиксированными параметрами ( J = 1; L P = 2 Y 1 = 1; y ₂ =- 1, Y 3 = 0,6; т ₂ -т , = 1,5- T ;

т 3 - _Т 1 = 3,5. T )_: 1 _— прием одиночных сигнальных элементов (отсутствие МСИ); 2 – демодуляция с помощью выравнивателя без обратной связи по решению; 3 – демодуляция с помощью выравнивателя при идеализированной ОСР; 4 – демодуляция с помощью выравнивателя при реальной ОСР.

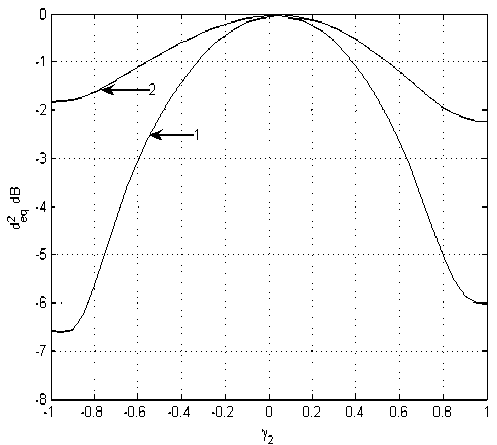
Рис. 6 Зависимость относительной эквивалентной метрики d _eq , определяемой (14), от амплитуды второго луча для одностороннего и двустороннего выравнивающих фильтров: 1 – в отсутствие ОСР (двустороннее выравнивание); 2 – при наличии идеализированной ОСР (одностороннее выравнивание).

Заключение

Таким образом, применение обратной связи по решению в демодуляторах с ограниченным интервалом анализа для каналов с МСИ дает следующие результаты.

Во-первых применение ОСР позволяет существенно упростить реализацию алгоритмов обоих типов: применительно к алгоритму переборного типа число перебираемых альтернатив снижается в M ^Q раз, а при использовании линейного выравнивателя длина выравнивающего фильтра и размерность матрицы системы уравнений определяющей вектор весовых элементов ВФ, сокращаются вдвое.

Во-вторых применение ОСР приводит к существенному увеличению расстояния между отдельными точками сигнального созвездия на приёме, что приводит к существенному улучшению помехоустойчивости (энергетический выигрыш составляет 2 дБ ^ 3.5 дБ при вероятности ошибки p = 10 ^-3 ).

С другой стороны, использование ОСР вызывает довольно сильный эффект размножения ошибок (энергетический проигрыш по сравне-ниюсослучаем идеализированной ОСР составляет 0.5дБ ^ 1дБ), что указывает на потенциальные возможности улучшения помехоустойчивости демодуляторов подобного типа.