Анализ влияния упругих деформаций космического аппарата на искажение формы отражающих поверхностей крупногабаритных элементов конструкции

О. П. Клишев, В. И. Халиманович

АНАЛИЗ ВЛИЯНИЯ УПРУГИХ ДЕФОРМАЦИЙ КОСМИЧЕСКОГО АППАРАТА НА ИСКАЖЕНИЕ ФОРМЫ ОТРАЖАЮЩИХ ПОВЕРХНОСТЕЙ КРУПНОГАБАРИТНЫХ ЭЛЕМЕНТОВ КОНСТРУКЦИИ

Проанализирована возможность использования традиционных уравнений движения упругого КА для расчетов среднеквадратичных отклонений отражающих поверхностей и представлен метод расчета изменения геометрических характеристик рефлекторов (линейных и угловых смещений вершины и изменения фокусного расстояния), обусловленных упругими деформациями их конструкции.

Одной из проблем динамики современных и перспективных космических аппаратов (КА) является анализ влияния упругих деформаций на искажения формы отражающих поверхностей крупногабаритных элементов конструкции, например, параболических рефлекторов.

Рассмотрим конструкцию космического аппарата, состоящую из корпуса и прикрепленных к нему упругих элементов (подконструкций), например, панелей солнечных батарей, антенн, телескопов и т. д. Корпусом будем называть часть конструкции, на которой расположена система управления движением КА, ее чувствительные элементы и двигательные установки, с помощью которых поддерживается заданная ориентация объекта в пространстве. Предполагается, что подконструкции крепятся к корпусу посредством идеальных либо упругих связей, которые представляются линейными пружинами с постоянными (квазипостоянными) жесткостными характеристиками. При движении КА возбуждаются малые упругие колебания, для описания которых может быть использована линейная теория упругости.

Расчет собственных форм и частот упругих колебаний всего КА или отдельных подконструкций может быть осуществлен методом конечных элементов.

Структура уравнений движения КА зависит от типа координатных функций, используемых для описания упругих смещений подконструкций, в качестве которых обычно выбираются собственные формы колебаний жестко закрепленной к корпусу КА подконструкции или собственные формы упругих колебаний всего КА.

Следует отметить, что использование той или иной системы координатных функций определяется не только простотой составления уравнений движения, но и точностью описания упругих свойств конструкции КА.

При использовании в качестве координатных функций собственных форм упругих колебаний отдельных подконструкций математическая модель движения КА с прикрепленными к нему A-упругими подконструкциями может быть представлена в следующем виде [1]:

тУ-Ьбн^а1] Pj = Fv;

Jto + LV + Ytip, = м-        (1)

7            .

Pi^iPi +V"Pl+alV, + blto = Qp1 / I ...A\ где m, L, J - масса, статический момент, тензор инерции недеформированного КА в связанной системе координат (ССК) соответственно; Fy, My - главные векторы и моменты управляющих сил, действующих на КА; aj, bj -прямоугольные матрицы коэффициентов инерционных связей между упругими колебаниями/-ой подконструкции и движением КА, рассчитанные относительно ССК; Qp - обобщенные силы, действующие нау-ую подконструкцию КА; н2, е - диагональные матрицы квадратов собственных частот и декрементов колебанийу-ой размерностью (n X n); К, щ - линейные и угловые скорости изделия;^ - матрица-столбец обобщенных координат характеризующих упругие колебания отдельных элементов конструкции КА.

Здесь предполагается, что корпус КА обладает большой жесткостью, и его можно считать твердым телом.

При использовании в качестве координатных функций собственных форм упругих колебаний всего КА его уравнения движения можно представить следующим образом [2]: ⋅ m V ° = L Fj ;

J и = , ;;

⋅⋅                 ⋅ q + Е q + Q2 q = L (^ F + ^Му);      (2)

⋅ v = vo + S^ Т qi;

i

⋅ ю=®о+£^ Т qi

X = J Vdt                (3)

ϑ=∫ ωdt где X, У - матрицы-столбцы размерностью (1 х 3) смещений и углов поворотов конструкции КА относительно инерциальной системы координат (ИСК); V, И - матрицы-столбцы размерностью (1 х 3), элементы которых проекции линейной и угловой скоростей движения корпуса на оси ИСК; V, Ио - матрицы-столбцы размерностью (1 х 3), элементы которых - проекции линейной и угловой скоростей корпуса как твердого тела на оси ИСК; £ i , £ m - матрицы собственной./-ой формы упругих колебаний КА и ее производной в произвольной точки т; £ у, £ j -матрицы собственнойу-ой формы упругих колебаний КА и ее производной в точке приложения управляющих усилий.

Указанные матрицы имеют следующие компоненты: ^-=⁽ u j , v j , w j ^),

^ =( %-, Vj, ej), где q - матрица-столбец обобщенных координат; Е, Q2 - диагональные матрицы декрементов и квадратов собственных частот упругих колебаний КА.

При расчете методом конечных элементов собственных форм и частот колебаний КА выбираются следующие условия нормировки:

[ ^ ]^т[М][ ^ ] = Г1.];

[ 5 ] ^т№ [ 5 I Г” ².|,                  (4)

где М и К - конечно-элементные матрицы масс и жесткостей конструкции.

Следует отметить, что для большинства существующих КА результаты численного моделирования динамики, полученные при использовании уравнений (1) и (2) совпадают или близки [3].

Рассмотрим КА, конечно-элементная модель которого представлена на рис. 1. КА состоит из твердого корпуса и прикрепленных к нему двух панелей солнечных батарей и крупногабаритного рефлектора. Будем учитывать только упругие деформации поверхности рефлектора, т. е. смещения и повороты его как твердого тела исключаются из рассмотрения.

Математическая модель движения КА (2) упругих деформаций рефлектора представляется в виде следующей системы независимых линейных дифференциальных уравнений второго порядка: ⋅⋅                            ⋅ qk + Еkqk + Qkqk = Qk,

Q k = M x % k + M y V 0 + M z e k ,

(^=1,2,_.,К), где q k - обобщенная координата, соответствующая к- й форме упругих колебаний (К- количество учитываемых форм); Q_k -обобщеннаясила; M x , M y , M z - управляющие моменты относительно осей x , y , z соответственно; Е _k, Q _k - коэффициент демпфирования и собственная частота упругих колебаний, причем

δΩ Е k = —, π где 5 - логарифмический декремент колебаний; %0,V0, e0 - формы поворотов КА вокруг центра масс при упругих колебаниях по тону к.

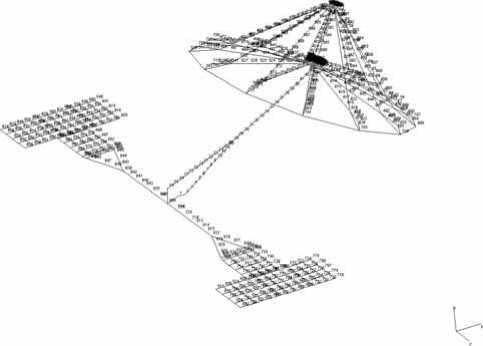
Рис. 1

Отметим, что уравнения являются независимыми, т. е. соответствующие им матрицы масс, демпфирования и жесткостей имеют диагональную форму.

При анализе, результаты которого приводятся ниже, учитывались только упругие деформации поверхности рефлектора, т. е. смещения и повороты его как твердого тела исключались из рассмотрения.

Рассматривается реакция упругой системы на управляющие моменты, меняющиеся по гармоническому закону:

M x , y , z = Mx, y , z ^SinQ t ^, где M x , _y , _z , Q - амплитуда и частота гармонического воздействия соответственно.

При этом комплексное значение обобщенной координаты q_k выражается следующим образом:

q =     Qk k Q2 -Q2 + iеkQ.

При Q = 0 получаем статическую реакцию системы на постоянные значения управляющих моментов.

Линейные смещения и угловые повороты КА выражаются следующим образом:

KKK

V о     V о о V о xо = zqkuk, yо = zqkvk, zk =zq^, k=1                    k=1                   k=1

Ф о = !А ф 0 , V o = i q . v 0 , e o = £ q k e k , k =1                    k =1                    k =1

где u^l° , v ⁰ , w ⁰ - формы смещений центра масс КА при упругих колебаниях по тону к .

В этих формулах и далее для простоты обозначений будем опускать над координатой q верхнее надчеркивание.

Линейные смещения и угловые повороты отражающей поверхности рефлектора в расчетных узлах записываются следующим образом:

KKK

^{x (} n ) = X Q k u k ⁽ n ), У ⁽ n ) = X S k v k ⁽ n )^, z ⁽ n ) = X № ⁽ n )^,

0 =1                            0 =1                            0 =1

KKK

Ф⁽ n ) = X 9 Ф 0 ⁽ n ^), V⁽ n ) = X 9 k v 0 ⁽ n ^{), 6(} n ) = X 9 k ⁶ 0 ⁽ n ^), 0 =1                             0 =1                            0 =1

где u₀ ( n ), v₀ ( n ), w₀ ( n ) - формы смещений в узле и при упругих колебаниях по тону к; ф ₀ ( n ), у ₀ ( n ), 6 ₀ ( n ) -формы поворотов в узле и при упругих колебаниях по тону к.

Средне-арифметическое относительное (относительно смещения и поворота корпуса КА) искажение поверхности рефлектора характеризует в основном смещение и поворот луча «в среднем». Оно вычисляется по следующим зависимостям:

1 n x = ~X (x(n) — xо),

N n =1

1N y=-X (y(n)-yо),

N n =1

1N z =XtX (z(n)-z0),

N n =1

1 N                                 (5)

Ф = —X ( Ф^{( n} )^-Ф o ) ,

N n =1

1N v , X (V(n)-Vo),

N n =1

N

6 = X (6( n ) -6 o ),

N n =1

где А - расчетное количество узлов, используемое для описания поверхности рефлектора.

Средне-квадратичное относительное искажение поверхности рефлектора характеризует в основном «расфокусировку» системы и выражается следующим образом:

1 N                ²

^х =    Xl ^{x ( n} ) - x о

N n =1

у = а LXl y ^{( n} )^- y ol

N n =1

N z=\hvXz(n)-zol, N n=1

- I 1 V I(

⁰ = 1й£1^ф n )-Ф о ,

V N n =1

1 N

Г =    X V n )-V o ,

N n =1

N

^ = A A X 6 n )- ⁶o| ■

N n =1

Операция | | означает модуль от комплексных чисел.

Рассмотрим метод расчета изменения геометрических характеристик параболического рефлектора (линей ных и угловых смещений вершины и изменения фокусного расстояния), обусловленных упругими деформациями конструкции КА.

Введем связанную с параболоидом систему координат (ОАТ2)_П (рис. 2). Точка О_п совпадает с вершиной параболоида.

Ось (ОА)П проходит через точку Оп и фокус параболоида, направлена от О к фокусу параболы.

Ось ( OY ) _n проходит через точку О_п, параллельна и соноправлена одноименной оси базовой системы координат

Ось (ОУ)П проходит через точку Оп, дополняет ПСК до правой.

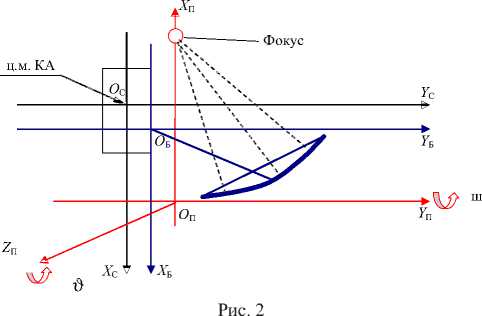
В системе координат Oxyz , связанной с параболоидом (нижние индексы _П здесь и далее опущены), уравнение его поверхности в недеформированном состоянии записывается в виде

2 px = y ² + z ² , где р - фокальный параметр.

Обозначим через x^ y i , z i координаты ряда точек (узлов), принадлежащих параболической поверхности. Можно считать, что координаты y i , z i задаются, а координаты x i = ( y i ² + z i ² )/(2 p ) вычисляются.

При упругих деформациях конструкции радиус-вектор Н₍ = ( x i , y i , z i ) какого-либо принадлежащего ей узла получает приращение 8Д (?) = (3 x i , 3 y i , 3 z i ) , зависящее от времени t.

Принимаем, что в каждый момент времени деформированная поверхность в некоторой системе координат Oxyyz может быть аппроксимирована параболической поверхностью:

2^-у2 + Р.

Значение фокального параметра при этом изменяется и может быть представлено в виде_р(t) = p + 3 p ( t ) .

Обозначим через 3R, (?) радиус-вектор от вершины О параболоида в недеформированном состоянии до вершины О аппроксимирующей параболиче с кой поверхности. Принимаем, что система координат Oxуz повернута относительно системы координат Oxyz на углы 3ф( t ), 3у( t ), 30? t ) вокруг осей ~ x , y , z соответственно.

В ортах системы координат Ox у z радиус-вектор??, (?) узла деформированной конструкции выражается следующим образом:

R, ^(R, +ЗД. -3^)-30 (R, +6R, -3^), где 36(?) = (Зф, Зу, 89).

Пренебрегая величинами второго порядка малости, это выражение запишем в виде

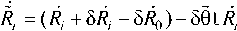
или в координатной форме:

X, (/) = Xj + Ьх, (?) -

-5^о (О - ^Nlt) + ^83(0,

уЛО = у, +§j,(0-

8а (7) + г,8фД(/) - ^8d(/) , z, (?) = z, + Sz, (f) -

-8z0 (/) - ^Зф^) + х,8ф(/)

Координаты каждого узла должны приближенно (в смысле среднего квадратичного отклонения) удовлетворять уравнение2 рх = у2 + z2- Подставим их в это уравнение и учтем, что координаты xi, yi, zi точно удовлетворяют уравнение 2px = y2 + z2 - В результате, опуская величины второго порядка малости, находим xi 8p - p 3x0 + yi 8у 0 + zi 8z 0 -

- z i ( p + x i )8ф + y i ( p + x i )8Д =

= - p 8 x i + y i 8 y i + z i 8 z i -

Полученное уравнение приближенно выполняется для каждого узла- Поэтому приходим к системе уравнений, которую представим в матричной форме:

Ай = В -

Элементы матрицы А и вектора b определяются по формулам ai1 = xi, ai 2 = - p, ai 3 = yi, ai 4 =

= zi, ai5 =-(p + xi )zi , ai6 = ( p + xi) yi bi = - p 8xi + yi 8yi + zi 8zi -

Координаты вектора и обозначают:

и₁ =8 p - вариация фокального параметра;

и ₂ = 8 x ₀;

u з =⁸ y 0 ;

и ₄ = 8 z ₀ - вариации координат вершины аппроксимирующей параболической поверхности при упругих колебаниях конструкции;

и ₅ = 8ф;

и ₆ = 8Д - углы поворота системы координат аппроксимирующей параболической поверхности при упругих колебаниях конструкции-

Вариации координат узлов при упругих колебаниях конструкции в выражении для вектора В определяются по формулам

N

8xi(t) = Xn ПТп(t), n=1

N

⁸ yi ⁽ t ) = X n Lp, ⁽ t ) , n = 1

N

⁸ z i ⁽ t ) = £ n n p,, ⁽ t ) ^, n =1

где p_n , ( n = 1,2,..., N ) -обобщенные координаты уравнений движения (1) КА с упругими элементами конструкции; п , , П У_п , П , - проекции собственной формы и упругих колебаний конструкции на оси x , y , z в узле i-

Применение метода наименьших квадратов приводит к системе 6-и уравнений:

А¹'Ай = А¹ В ,                   (7)

где A T - транспонированная матрица-

Решение уравнений (7) определяют параметры аппроксимирующего параболоида таким образом, что средне-квадратичные отклонения его поверхности от деформируемой отражающей поверхности рефлектора будут минимальными-

Совместное решение уравнений (1) и (7) определяет обусловленные упругими деформациями линейные и угловые смещения вершины и изменения фокусного расстояния параболического рефлектора при действии управляющих моментов-