Анализ возможностей ахроматизации оптических систем, состоящих из дифракционных элементов

Совершенствование оптических систем, освоение новых, нетрадиционных для оптики спектральных областей требует и нетрадиционных подходов к коррекции хроматизма. Действительно, в системах, предназначенных для видимого диапазона, преимущественной элементной базой которых являются рефракционные линзы, основным приемом исправления хроматизма является использование материалов с различной дисперсией [1]. Однако возможности такого приема существенно ограничены, а их расширение требует использования необычных оптических материалов, которые являются весьма дорогими и имеют, как правило, невысокие эксплуатационные характеристики [2, 3].

С другой стороны, включение в оптическую систему наряду с рефракционными линзами дифракционных оптических элементов (ДОЭ) позволяет как упростить систему, так и отказаться от использования необычных оптических материалов [4-6]. Проблема построения ахроматизированных оптических систем на базе рефракционных линз еще более усугубляется вне видимого диапазона электромагнитного спектра: в инфракрасной (ИК), ультрафиолетовой (УФ), вакуумной ультрафиолетовой (ВУФ) и рентгеновской областях. В дальней ИК- и ВУФ-областях это связано с тем, что каталог используемых материалов ограничивается несколькими единицами [7], а в рентгеновской области – характерными для нее особыми свойствами материалов [8].

В результате рефракционные линзы жесткого (коротковолнового) рентгеновского диапазона должны быть ограничены преломляющими поверхностями с радиусами кривизны в их вершине, составляющими доли микрометра [9]. Что же касается мягкого (длинноволнового) рентгеновского излучения, то его проникающая способность во все вещества, включая воздух, очень мала и не превышает нескольких микрометров [10]. Это, наряду с очень малыми радиусами кривизн преломляющих поверх- ностей, практически исключает использование рефракционных линз в длинноволновой части рентгеновского диапазона. Таким образом, один из немногих альтернативных путей ахроматизации оптических систем мягкого рентгеновского диапазона состоит в построении их на основе ДОЭ.

Проблеме ахроматизации чисто дифракционных оптических систем посвящен ряд работ (см., например, [11-14]), и, в частности, в работе [14] найдены четыре схемы дифракционных дублетов, скоррегиро-ванных на две длины волны. Общим для всех этих схем является то, что, в отличие, например, от зонных пластинок Френеля, используемые в схемах ДОЭ имеют ненулевую пространственную частоту в центре их структуры, т.е. являются аксиконами. При этом возможности дифракционных ахроматизированных дублетов, а также сопоставительный анализ фокусирующих свойств систем различных типов приведены для ИК-диапазона (длина волны порядка 10 мкм), когда отношение светового диаметра к длине волны составляет величину порядка 104. В рентгеновском же диапазоне это отношение как минимум на два порядка больше. Данное отношение входит в волновую сферохроматическую аберрацию, выраженную в долях длины волны, и определяет качество фокусировки [15-17]. Поэтому, чтобы оценить возможности использования дифракционного дублета для фокусировки полихроматического излучения рентгеновского диапазона, требуется провести дополнительные исследования. Кроме того, несмотря на последние успехи в лазерной и электронной литографии, в принципе позволяющие изготавливать ДОЭ как для всех поддиапазонов оптического (включая ИК и УФ) [18], так и рентгеновского излучения [19-22], величина минимального периода в структурах элементов оптической системы во многом определяет как достижимую дифракционную эффективность, так и стоимость или даже саму реализуемость системы. Поэтому в данной работе предлагается методика получения функций распределения простран- ственных частот ДОЭ, позволяющая ахроматизировать систему, рассматривая минимальный период в качестве свободного параметра.

Расчет структур ДОЭ

Из четырех представленных в [14] схем наиболее интересной с точки зрения построения на ее основе фокусирующего объектива, рассчитанного на полихроматическое излучение, является схема, представленная на рис. 1 и отличающаяся тем, что в ней некольцевую апертуру имеет первый ДОЭ, а максимальные пространственные частоты дифракционных структур элементов имеют наименьшие значения.

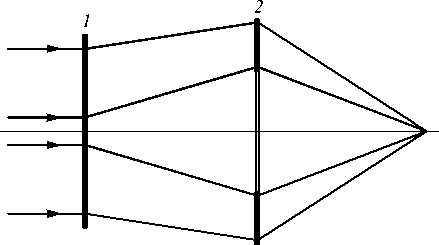
Рис. 1. Оптическая схема дифракционного дублета, скоррегированного на две длины волны: 1, 2 – ДОЭ

При построении алгоритма, позволяющего получить функции распределения пространственных частот ДОЭ, обеспечивающие ахроматизацию фокусирующего объектива, будем считать, что оба ДОЭ работают в первом порядке дифракции, а спектральный диапазон, в пределах которого производится ахроматизация, ограничен длинами волн Л' и Х>Л .

Учитывая, что первый ДОЭ представляет собой аксикон с дополнительными фокусирующими свойствами, а также с целью минимизации числа параметров, определяемых итерационно, в качестве его пространственной частоты примем частоту структуры «обратной» осевой асферизованной голограммы точки

^Q 1 ^(р 1 ) = Л Z 1 ^{C р} 1

Л I

I

qh (pi)- 5 Bi pi-2

i = 1

Здесь p 1 - расстояние от оси структуры в плоскости первого ДОЭ, Q _H ( p 1 ) - сомножитель пространственной частоты осевой голограммы точки, зависящий от расстояний от плоскости регистрации до соответствующих источников записи z ₁ и z ₂ , т.е. отрезков записи первого ДОЭ, определяющих его оптическую силу [15, 16]:

Q н ( P i ) = - ,    ^{1 1}     2 + ,    ^{1 2}     2

V1 + (P1/Z1 )    V1 +(P1/z 2 )

Сразу же отметим, что при работе объектива с бесконечно удаленным предметом z1 = -^ , а z2 це- лесообразно положить равным трем-пяти задним фокальным отрезкам объектива.

Слагаемое в формуле (1), пропорциональное

I

5 B i P i ^- 2 , обеспечивает асферизацию формируемо- i = 1

го этим ДОЭ волнового фронта, а константа

(

^C = B O ^p 1,max I ^Q H ^(p 1,max ) 5 ^{B P} 1,max I              ⁽³⁾

V                    i=1            J обеспечивает «обращение» пространственной частоты, т.е. ее рост не от оси к краю апертуры ДОЭ, а наоборот.

В формуле (3) р 1, _тах - радиус апертуры первого ДОЭ, а коэффициент B ₀ определяет расстояние от оси, т.е . центра симметрии структуры, до окружности, на которой пространственная частота структуры обращается в нуль и, как показали исследования, является весьма эффективным коррекционным параметром, влияющим на минимальный период в структуре элементов дублета и его хроматические свойства.

Выбрав функцию распределения пространственной частоты первого ДОЭ в соответствии с формулой (1), поиск значений коэффициентов B ₁ , …, B_I осуществляют итерационно. Соответствующий процесс, целью которого является получение структур ДОЭ, обеспечивающих фокусировку излучения на обеих выбранных длинах волн в одну и ту же фокальную точку, строится на основе прогона хода лучей в плоскости y0z (см. рис. 2) следующим образом.

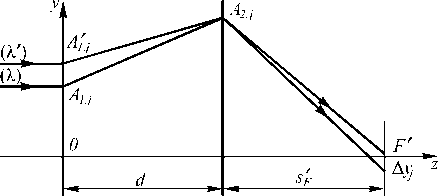
Рис. 2. К расчету пространственной частоты структуры второго ДОЭ

Для расчета хода лучей использются формулы (1)-(3). При этом через некоторую точку первого ДОЭ A 1,j с координатой y_k j на длине волны Л из предметной точки, лежащей на оси 0z и отстоящей от первого ДОЭ на конечном или бесконечном расстоянии z ₁ , прогоняется луч до пересечения со вторым ДОЭ в точке A _{2, j} с координатой y _{2, j} , которую соединяют с фокальной точкой объектива F' .

Затем итерационно на первом ДОЭ находят такую точку А ₁ ‘ j , проходя через которую луч на длине волны Л‘ также попадет в точку A ₂ j- . Направляющие косинусы этого луча и прямой A_2jP' определяют значение пространственной частоты микроструктуры второго ДОЭ в точке A _{2, j} :

ρ 2, j ( l 1, j ^- l 2, j )

Ω2,j(ρ2,j) = , (4) λ y2,j где l1,j и l2,j – направляющие косинусы луча A1′, jA2, j и прямой A2,jF′ относительно оси OY [23].

Далее, используя значение пространственной частоты Ω _{2, j} ( ρ _{2, j} ) , находят точку пересечения с фокальной плоскостью луча на длине волны λ , проходящего через точки A _{1, j} и A _{2, j} и дифрагирующего на втором ДОЭ. Отклонения от фокуса ∆ y_j , полученные для набора лучей, заполняющих апертуру первого ДОЭ, используются для построения целевой функции, из условия минимизации которой итерационно находятся оптимальные величины коэффициентов B_i ( i = 1, ..., I ). В качестве целевой функции может быть использован, например, среднеквадратический радиус диаграммы рассеяния лучей δ _RMS , а итерационный процесс построен на основе модернизированного метода Ньютона [24].

После завершения итерационного процесса по набору дискретных значений Ω _{2, j} ( ρ _{2, j} ) методом наименьших квадратов находят коэффициенты полинома, описывающего пространственную частоту второго ДОЭ:

Ω 2 ( ρ 2 ) = ∑ C j ρ 2 ^{j - 1}. (5) j = 1

Исследование дифракционного дублета-ахромата

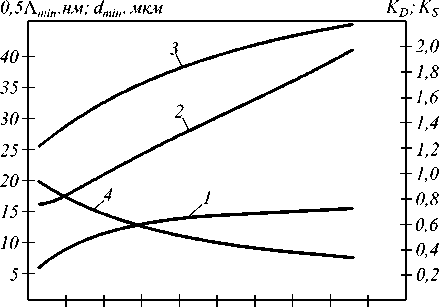
Результаты исследования взаимозависимости основных параметров фокусирующего дифракционного дублета-ахромата представлены на рис. 3. Здесь d _R = d s ′ _F – отнесенный к заднему фокальному отрезку промежуток между двумя ДОЭ; Λ _min – минимальный период в квазипериодических структурах первого и второго ДОЭ; δ _RMS – среднеквадратический радиус диаграммы рассеянии лучей на центральной длине волны λ _c спектрального диапазона от λ′ до λ ; K _D = D ₂ D ₁ – отношение световых диаметров второго и первого ДОЭ; K _S – коэффициент заполнения апертуры второго ДОЭ, вычисляемый по формуле

K _S = 1 - ( D ₂ ^(int) D ₂ ^(ext) ) ², (6) где D ₂^(int) и D ₂^(ext) – внутренний и внешний диаметры кольцевой апертуры второго ДОЭ.

Результаты, представленные на рис. 3, получены для λ′ =5 нм, λ _c =5,5 нм, λ =6 нм, светового диаметра первого ДОЭ D ₁ =3,5 мм и при относительном отверстии дублета, под которым в данном случае можно понимать отношение светового диаметра D ₁ к заднему фокальному отрезку s_F ′ , равное 0,1.

а)

б)

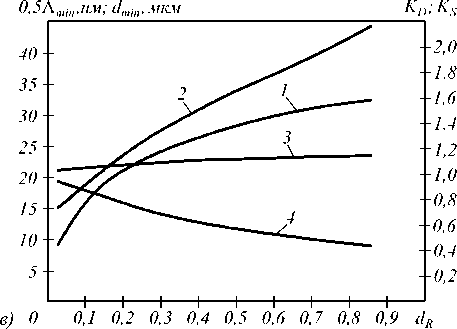
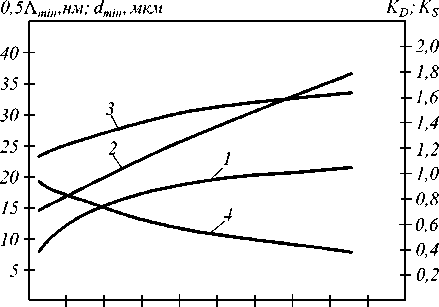
Рис. 3. Графики взаимозависимости основных параметров фокусирующего дифракционного дублета-ахромата (а – при B ₀ =3; б – при B ₀ =2; в – при B ₀ =1,2):

1 – Λ _min ( d_R ) ; 2 – δ _RMS ( d_R ) ; 3 – K_D ( d_R ) ; 4 – K_S ( d_R )

При выбранных параметрах итерационный процесс получения оптимальных распределений пространственных частот ДОЭ, завершавшийся при достижении требуемого качества фокусировки лучей на длине волны λ ( δ _RMS ≤ 100 λ ), достаточно быстро сходился даже в случае нулевых начальных значений коэффициентов B ₁ , …, B_I ,. Причем требуемое качество фокусировки легко достигалось уже при I =7.

Как видно из представленных на рис. 3 кривых, минимальный период в структуре Λmin увеличивает- ся с уменьшением коэффициента B0 и с ростом промежутка dR между ДОЭ дублета. Среднеквадратический радиус диаграммы рассеяния лучей δRMS на центральной длине волны λc уменьшается с уменьшением промежутка dR между ДОЭ. Что же касается зависимости δ от B , то она не является моно-RMS 0

тонной и оптимальное значение, обеспечивающее минимум δ _RMS , лежит внутри диапазона 1,2 <  B ₀ <  3 .

Относительный световой диаметр второго ДОЭ K _D растет с увеличением промежутка между ДОЭ, но скорость его роста с уменьшением коэффициента B ₀ резко замедляется. Наконец, коэффициент заполнения апертуры второго ДОЭ K _S уменьшается с ростом промежутка между ДОЭ дублета и слабо увеличивается с уменьшением коэффициента B ₀ .

Результаты исследований, выполненных для ряда относительных отверстий, показали, что при неизменном световом диаметре первого ДОЭ увеличить минимальный период в структуре элементов Λ _min , практически не увеличивая при этом размер диаграммы рассеяния лучей, можно путем увеличения габарита дублета, т.е. одновременного увеличения в одинаковое число раз величин d _R и s_F ′ . Уменьшение же среднеквадратического радиуса диаграммы рассеянии лучей на центральной длине волны λ _c достигается лишь за счет уменьшения светового диаметра первого ДОЭ, что характерно для любой оптической системы, состоящей из дифракционных линз.

Заключение

В заключение сопоставим основные характеристики дифракционного дублета-ахромата с соответствующими характеристиками одиночной дифракционной линзы (ДЛ). Минимальный период в структуре ДЛ при относительном отверстии D/s_F ′ ≤ 0,2 с высокой степенью точности может быть рассчитан по формуле

2%

Λ min = ^{2 λ c} .                                     (7)

^D / s _F ′

Следовательно, при λc =5,5 нм и DIsF′ =0,1 минимальный период в структуре ДЛ Λmin =110 нм, что значительно превышает минимальный период в структурах ДОЭ дублета-ахромата практически при любых возможных сочетаниях коррекционных параметров B0 и dR . В то же время, если ДЛ формирует дифракционно-ограниченное изображение на длине волны λc , то на длинах волн λ′ =5 нм и λ =6 нм при D =3,5 мм среднеквадратический радиус пятна рассеяния лучей δRMS ≈ 120 мкм. Таким образом, при выбранных параметрах по пятну рассеяния монохроматического излучения, лежащего в пределах спектрального диапазона от λ′ до λ , дублет-ахромат дает по сравнению с одиночной ДЛ выигрыш как минимум в 2,7 раза.

Для сравнения возможностей фокусировки полихроматического излучения дублетом-ахроматом и одиночной ДЛ рассмотрим дублет с минимальным периодом в структурах Λ _min =54 нм [ B ₀ =1,2; d _R =0,43 (рис. 3 в )]. Ширину спектрального диапазона определим из условия равенства среднеквадратических радиусов диаграмм рассеяния лучей монохроматического излучения в центре диапазона и на его краях. Для дублета с выбранными параметрами этот диапазон ограничен длинами волн 4,85 нм и 6,15 нм, а среднеквадратический радиус диаграммы рассеяния лучей полихроматического излучения в пределах этого диапазона δ _RMS =24 мкм. При фокусировке же полихроматического излучения указанного спектрального диапазона одиночной ДЛ с D =3,5 мм среднеквадратический радиус диаграммы рассеяния δ _RMS =99 мкм, т.е. при фокусировке полихроматического излучения данный дублет-ахромат дает выигрыш по сравнению с одиночной ДЛ более чем в 4 раза.