Анализ возможности экономии тепловой энергии при прерывистом режиме отопления
Автор: Панферов Владимир Иванович, Анисимова Елена Юрьевна
Рубрика: Инженерное оборудование зданий и сооружений
Статья в выпуске: 12 (112), 2008 года.
Бесплатный доступ
Рассмотрена задача оптимального управления тепловым режимом здания в нерабочее время. Найден алгоритм оптимального управления режимом прерывистого отопления. Уточнена область допустимых решений критерия оптимальности управления. Проведен анализ экономии энергии при использовании прерывистого отопления.
Короткий адрес: https://sciup.org/147154192
IDR: 147154192 | УДК: 669.074
Текст научной статьи Анализ возможности экономии тепловой энергии при прерывистом режиме отопления
В условиях рыночной экономики и значительного повышения цен на энергоресурсы особую значимость приобретает задача эффективного использования тепловой энергии в системах теплоснабжения зданий. Поэтому актуальными являются исследования в области оптимального управления тепловым режимом здания, в частности, режимом прерывистого отопления.
Известно, что в жилых, общественных, административно-бытовых и производственных зданиях в нерабочее время температуру воздуха можно поддерживать на более низком уровне, чем в остальные промежутки времени. Это дает возможность сэкономить расход энергии на отопление. Однако для получения максимального эффекта от реализации такого, так называемого режима прерывистого отопления необходимо решить задачу об оптимальном управлении этим режимом. Рассмотрим постановку этой задачи.
Как нами установлено [1, 2, 3], температурный режим помещения удовлетворительно может быть описан следующим дифференциальным уравнением:
T^l+e^ = kw^, (1)
ат где 0(г) - избыточная температура, У(т)=?в(т)-Гн(г), /в(т), /н(г) - соответственно температура внутреннего и наружного воздуха, Т - постоянная времени, И^о (г) — мощность системы отопления, т -время, к - коэффициент передачи.
Количество теплоты, израсходованной системой отопления, оценивается функционалом гн
1=^т^т, (2)
о где гн - заданное время.
Задача оптимального управления тепловым режимом формулируется следующим образом [4]: требуется найти такое управление мощностью системы отопления Иц (г) , которое переводило бы объект управления (1) из заданного начального состояния 0(0) = 0О в заданное конечное состояние 0(гн)=0к за заданное время тн , при этом расход теплоты I системой отопления был бы минимальным. Формально это записывается так:
1 min •
Мощность системы отопления должна при этом удовлетворять следующему ограничению:
И^п<^о(т)<^оу, (3)
где Wq - установленная мощность системы отопления, Жд™11 - минимальная мощность системы отопления, как рекомендуется работой [5], эта мощность должна обеспечить поддержание температуры внутреннего воздуха на уровне 12 °C, исключающем выпадение конденсата на поверхностях ограждений.
В работе [6] формулировалась аналогичная задача оптимального управления, однако при решении этой задачи предполагалось, что температура внутренних поверхностей ограждений «...задана и сохраняет постоянное значение в период натопа». Заметим, что данное допущение, как это нетрудно видеть, означает, что ограждающие конструкции здания, отличающиеся наибольшей теплоемкостью из всех участников теплообмена, никак не влияют на решение поставленной задачи, т.е. на выбор оптимального управления. Далее в работе утверждается, что исходная условная задача сводится к некой безусловной задаче, экстремалями которой являются прямые линии, т.е. в опти- мальном процессе /в(г) должна быть линейной функцией времени. Затем авторы, полагая дополнительно, что во время натопа и температура наружного воздуха является константой, из модели процесса находят, что оптимальное управление -мощность системы отопления тоже должно быть константой. После этого в работе [6] делается совсем нелогичный вывод, что «...оптимальность управления означает минимальность времени» натопа помещения и авторы переходят к рассмотрению задачи о максимальном быстродействии. Конечно, можно продолжить рассмотрение всех особенностей указанной работы, однако в этом нет большого смысла: уже отмеченные замечания делают сомнительным обоснованность выводов, поэтому достаточно смело можно утверждать, сформулированная выше задача оптимального управления еще не решена.
Кстати говоря, из выводов работы [6] следует, что оптимальное управление имеет только один интервал постоянства, кроме того, авторы, no-видимому, не различают понятия времени натопа и времени максимального быстродействия. Время натопа (разогрева помещения) может значительно превышать время максимального быстродействия, время максимального быстродействия - это минимально возможное время, за которое можно «натопить» помещение до заданной температуры.
В работе [7] оценивается эффективность режима максимального быстродействия, причем одним из декларируемых авторами тезисов является утверждение о том, что «разогрев ...необходимо начинать с разогрева наиболее теплоемких частей помещения». Вместе с тем, как уже это отмечалось, при отыскании оптимального управления авторы в [6] полагали, что температура внутренних поверхностей ограждений «...задана и сохраняет постоянное значение в период натопа». Таким образом, наблюдается явное противоречие между допущениями, принятыми при решении задачи, и тем, что рекомендуется при практическом использовании, якобы, этого решения. В целом, создается впечатление, что авторы, поставив, но, в общем-то, так и не решив задачу (как следует из материалов работы [7], это они поняли и сами), либо позаимствовали то, что давно было известно, например, в металлургической теплотехнике из результатов задач оптимального управления нагревом металла, эти результаты были обобщены, в частности, в работах [8, 9], либо высказали свои интуитивные соображения.
Однако вернемся к рассмотрению поставленной задачи и подчеркнем, что для режима прерывистого отопления данная задача имеет следующую особенность: в начале и в конце рассматриваемого промежутка времени [0, тк] избыточная температура 6 (г) должна быть равна одному и тому же значению 0О, такова особенность режима прерывистого отопления.
Для решения поставленной задачи нами была использована теория оптимального управления [10], согласно которой оптимальное управление в данной задаче будет представляться кусочнопостоянной функцией, принимающей граничные значения.
Для простоты будем считать, что продолжительность нерабочего времени такова, что в графике Ид (г) есть два интервала постоянства и что длительность этих интервалов одинакова. Мощность системы отопления для первого интервала обозначим через W0l, а для второго интервала — через JF02 . Так как за время режима прерывистого отопления избыточная температура 0(т) должна измениться от заданного начального значения 0О до требуемого конечного значения 0О, по какой-либо пока не известной траектории, то на основании (1) получается следующее уравнение, связывающее 1Т01 и 1К02:
^02+^01.(1-а) = 60(2-а), (4)
где а=1-ехр(-тн/(2Т)).
Функционал I преобразуется в обычную функцию двух переменных 1FO1 и Wm и будет иметь вид:
^=^0iy + ^02y. (5)
Здесь общий множитель гн/2 можно просто опустить, так как он не влияет на результаты решения задачи, т.е. на ответ.
Таким образом, поставленная задача оптимального управления свелась к условной задаче нелинейного программирования: требуется найти минимум функции I, заданной уравнением (5), при условии, что ее аргументы JF01 и Ж02 должны удовлетворять соотношениям (3) и (4):
min > <6)
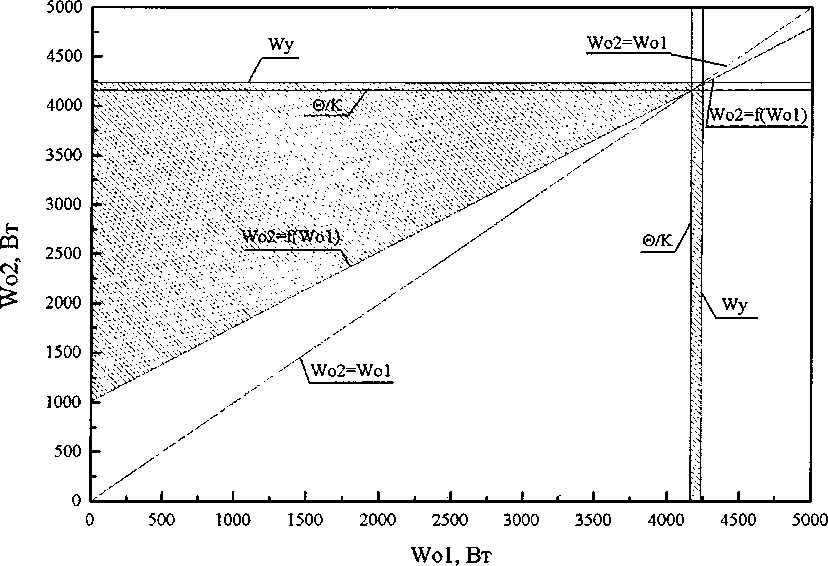
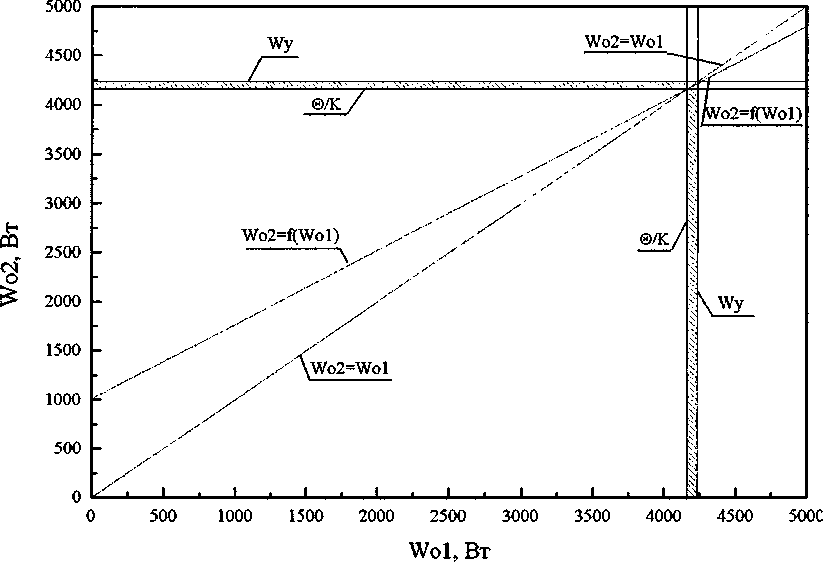
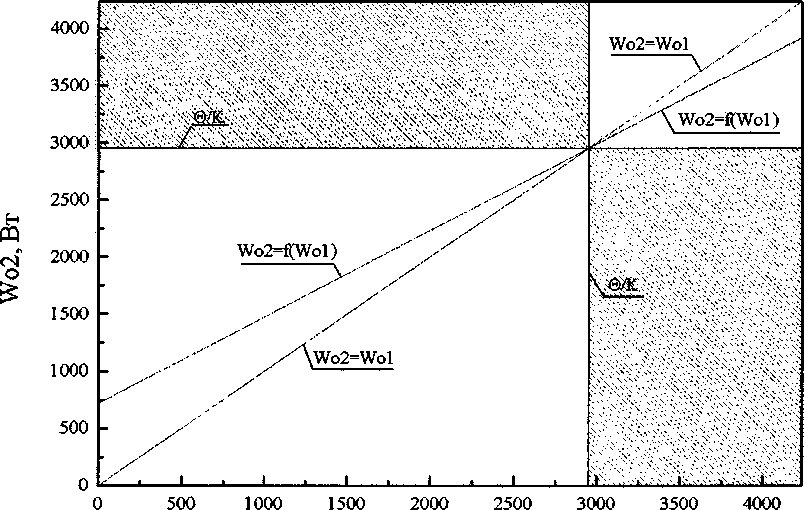
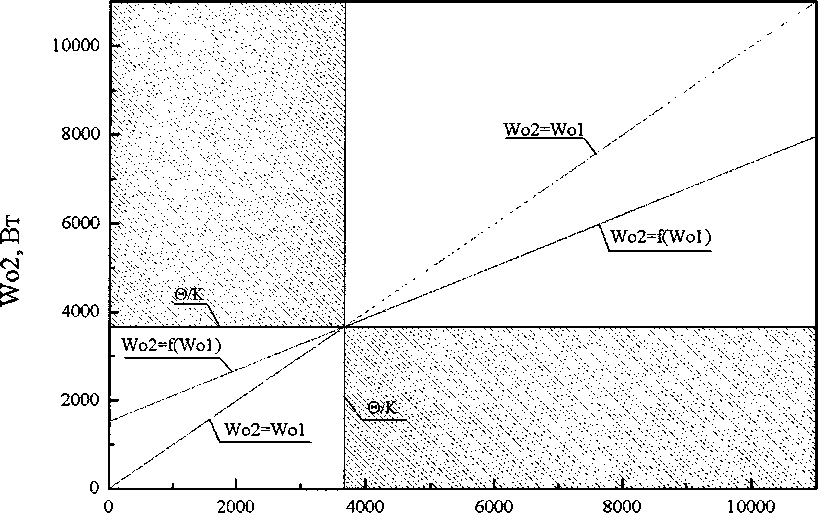
W^W^eG где О>Г ^W01,Wto Заметим, что исходную задачу неклассического вариационного исчисления можно свести к точно такой же задаче нелинейного программирования и другим способом, а именно методом параметризации функции управления, конкретно представляя ее состоящей из двух дискрет одинаковой длительности [11]. Для решения сведем условную задачу оптимизации (6) к безусловной методом подстановки, для этого из уравнения (4) выразим, например, Жо2 через 1Г0] и подставим в критерий (5), тогда будем иметь, что I = 0o^UaWol. (7) к Учитывая, что коэффициент а в реальных условиях удовлетворяет неравенству 1 > a >0, из (7) найдем, что чем меньше мощность системы отопления на первом интервале постоянства, тем экономичнее режим, следовательно, на первом интервале мощность системы отопления должна быть равна И^™'". Примечательно, что если из (4) выразим Ж01 через Ж02 и подставим в критерий оптимальности, тогда задача оптимизации будет иметь вид: / = min ' (8) -а) (1 — a) w<)2 Из последнего соотношения следует: чем больше величина Ж02, тем меньше величина I. Однако при этом следует учитывать ограниченность области допустимых решений. Если Ж01 уменьшать до нуля, то в этом случае из уравнения (4) следует, что Ж02 можно увеличивать только до значения %2= 0о(2-а)/к. При этом будет достигаться минимально возможное значение критерия I = OQ—j—. Если же Ид] разрешается уменьшать лишь до значения %тт, то в этом случае, как это следует из (4), И^02 можно увеличивать только до значения ^02 = ^о (2 - а)/^ ~ W^m (1 ~ а), достигаемое при этом значение критерия увеличится и составит уже величину I = 0О -—- + ай^™” . к Если полагать, что ^02 = W^, то мощность системы отопления можно снижать лишь до следующей величины: ^01 = [^(2-а)-^]/[Л(1-а)] . Достигаемое три этом значение критерия будет равно 7 = 6Ь^^-^о'—• 0 к0 (1-а) Так как 1 - а > 0, то из вышеизложенного следует, что самым экономичным является режим, когда 1Г02 = Wj , а ^О1=[бо(2-а)-^]/[А(1-а)] (3-й случай), то есть на втором участке мощность системы отопления поддерживается на максимальном уровне, а на первом участке управления ее мощность выбирается из условия попадания в заданную температуру 0О перед началом рабочего дня в здании [12]. Таким образом, сначала для простоты решения задачи мы полагали, что длительность интервалов постоянства управления одинакова, однако на самом деле это далеко не всегда так, длительность интервалов постоянства в общем случае должна быть различной. Теперь выясним, какой должна быть длительность каждого интервала, с тем, чтобы в начале и в конце процесса температура была бы равна 0О. Решение задачи оптимального управления в такой постановке, вероятнее всего, даст больший эффект. Обозначим длительность первого интервала через тх, а второго - через т2 . Очевидно, что эти величины связаны следующими соотношениями: ^02 ~г2 1-ет [Т,+Т2=ГН + ^01 ~г2 е т -1 + а =а0о где 1Е01 = С™ - минимальная мощность системы отопления, Wq2 = W^ - максимальная, установ- ленная тепловая мощность, а = 1 - expl —^- I. Найдем из первого уравнения системы (9) выражение для определения г2: г2 = -Г • In к ww-wm Из второго уравнения системы (9) найдем, что продолжительность первого интервала времени будет определяться следующим образом: г, = тк + Г ■ In к ^01 ~ ^02 (И) Функционал I в этом случае будет иметь вид: 7 = 1FO1 тк + Т • In 1 + V х wox-wto +^2 -Tin a®° aW к 01 1 + -*------- ^01-^02 Из (12) следует, что в отличие от предыдущего случая (предыдущей постановки задачи оптимального управления) критерий оптимальности будет уже нелинейной, точнее трансцендентной, функцией аргументов Ж01, 1FO2. К этому критерию необходимо было присоединить область допустимых решений, вытекающую из постановки задачи. Область допустимых решений определяется следующими условиями: - когда выражение, содержащееся под знаком логарифма, будет положительным, то есть ^oi-^+^j-^o. ^01-^02 - когда значение продолжительности второго промежутка времени будет положительным или равным нулю, то есть г2>0; (14) - когда значение продолжительности первого промежутка времени (времени остывания) будет положительным или равным нулю, то есть ^>0; (15) -ограничения, накладываемые на значения мощностей системы отопления Ж™п0<^01,^02<^. Проанализируем каждое из вышеприведенных ограничений. Рассмотрим ограничения, накладываемые на область допустимых решений, условием (13). Выражение (13) будет иметь положительное значение в двух случаях: 1) когда - ^01 - ^02 > 0; 2) когда - W01-W02*a\^-Wm ^01 ~ ^02 < 0- В результате учета ограничений (16), область допустимых решений будет определена условиями (18Н19): W <^ - 01 к ’ (18) .^o2<^oi; wm С учетом выражения (17), область допустимых решений будет ограничена условиями (20)—(21): W < — ^02>^01(1-а)+^; .^02 >^0Г Таким образом, исходя из условий (16) и (17) область допустимых решений для уравнения (12) будет иметь вид, представленный на рис. 1. Данная область построена для здания с теплотехническими характеристиками, отвечающим требованиям [13]. Установленная мощность системы отопления равна W^ =4236Вт, избыточная температура 0О=55°С, к = 0,013 °С/Вт, тогда в0/к =4230,8 Вт. Не трудно заметить, что значение коэффициента 00(к, при котором происходит изменение условий ограничения, очень близко к величине установленной тепловой мощности. Рассмотрим ограничения, накладываемые на область допустимых решений, вытекающие из условия (14). Продолжительность второго проме- Рис. 1. Область допустимых решений уравнения функционала / с учетом ограничения (13), для здания, отвечающего требованиям СНиП по теплотехническим показателям жутка времени, должна быть положительной или равной нулю, то есть В результате решения неравенства (25) выяв ляются следующие ограничения: -Tin к 01 1+-£----- ^01 ~ ^02 Данное выражение будет ное значение в двух случаях: ^01 ^01 "02 > к ’ иметь положитель- "02> к ’ №1 ^01 "02> к Тогда область допустимых решений с учетом прежних (18)—(21) и вновь полученных ограничений (23)-(24) будет иметь вид, представленный на рис. 2. Область построена для вышеприведенного здания, и представлена заштрихованными площадями. Очевидно, что происходит сокращение области допустимых решений до трех зон. Наконец, рассмотрим ограничения, накладываемые на область допустимых решений, вытекающие из условия (15). Продолжительность первого промежутка времени должна быть положительной или равной нулю, то есть гк+Т-1п 1+------- >0. (25) к Wx-W2 ^01 -^02’ Тогда область допустимых решений с учетом прежних (18)—(21), (23)-(24) и вновь полученных ограничений (26)-(27) будет иметь вид, представленный на рис. 3. Область, построенная для вышеприведенного здания, сокращается до двух зон, представлена заштрихованными площадями. Однако данная область может быть расширена в некоторых случаях, например, при уменьшении величины избыточной температуры, а также при увеличении располагаемой мощности системы отопления. Расширение пределов области происходит вследствие того, что значение максимальной расчетной тепловой мощности остается прежним, а значение избыточной температуры 9 (а именно температуры наружного воздуха) - уменьшается по сравнению с расчетной температурой для проектирования системы отопления, следовательно, происходит снижение теплопотерь здания. Таким образом, появляется дополнительный резерв мощности системы отопления для разогрева здания, что позволяет расширить пределы регулирования тепловой мощностью. Подобную ситуацию можно проиллюстрировать рис. 4. Для расчета применя- Рис. 2. Область допустимых решений уравнения функционала / с учетом ограничений (13Н14) Рис. 3. Область допустимых решений уравнения функционала / с учетом всех ограничений при и0 = 55 °C Wo1,Bt Рис. 4. Область допустимых решений уравнения функционала / для избыточной температуры и0 = 39 °C лось ранее рассмотренное здание. На графике изображена область определения функционала I для избыточной температуры 0О = 39 °C . Схожая ситуация может наблюдаться для здания, имеющего завышенную установленную тепловую мощность. Область определения функционала I в этом случае показана на рис. 5. Данная область построена для здания со следующими теплотехническими характеристиками: расчетная мощность системы отопления равна Wq =3668,5Вт, располагаемый диапазон изменения значений тепловой мощности составляет Wo е[0;11 000 Вт], избыточной температурой У0=55°С, к = 0,015 °С/Вт, Wo1,Bt Рис. 5. Область определения функционала / в случае, когда здание имеет завышенную установленную тепловую мощность тогда 0^/к = 3666,7 Вт. На практике подобное возможно после утепления здания, подключенного к автономному источнику теплоты. В этом случае теплотехнические характеристики здания улучшаются, расчетная тепловая мощность W^ уменьшается, а располагаемый диапазон регулирования мощности системы отопления останется неизменным (при условии, что автономный источник теплоты остался прежним). Заштрихованные зоны на рис. 5 являются областями допустимых решений функционала I. Полученные области ограничены условиями (13)—(15). Таким образом, была найдена область допустимых значений функционала / для зданий с разными теплотехническими характеристиками, а также различными параметрами источника теплоты на вводе в здание. Как уже отмечалось, критерий оптимальности (12) - это нелинейная функция аргументов 1701 и 1Г02 . Решить задачу оптимизации критерия I аналитическим путем не представлялось возможным, поэтому для решения этой задачи была написана программа на языке C++, в которой применялись методы покоординатного спуска и золотого сечения. Оптимальное управление в каждом конкретном случае находится путем использования разработанной программы. Программа по определению оптимального режима прерывистого отопления имеет удобный пользовательский интерфейс. В качестве исходных данных заносятся: продолжительность нерабочего времени, избыточная температура, диапазон изменения мощности системы отопления. Результаты расчетов выводятся в большом окне. В результате вычислительных экспериментов подтвердился ранее полученный вывод о том, что функционал, I, оценивающий количество теплоты, израсходованной системой отопления, тем меньше, чем меньше тепловая мощность на первом промежутке времени и больше на втором. Далее для различных температур наружного воздуха была определена эффективность разработанного режима прерывистого отопления для случая, когда здание имеет автономный источник теплоты. Оказалось, например, что при температуре наружного воздуха -18 °C и продолжительности нерабочего периода 15 часов оптимальный режим прерывистого отопления для выбранного здания экономичнее по расходу теплоты на 6,4 % по сравнению с обычным режимом отопления. При температуре наружного воздуха -5 °C эта экономия составит 9,3 %. При этом установлено, что применение режима прерывистого отопления в зданиях, подключенных к центральным тепловым сетям, не дает существенной экономии тепловой энергии [4, 14, 15]. График отопления здания в течение суток, включая режим оптимального управления в нерабочее время, приведен в работах [14-16].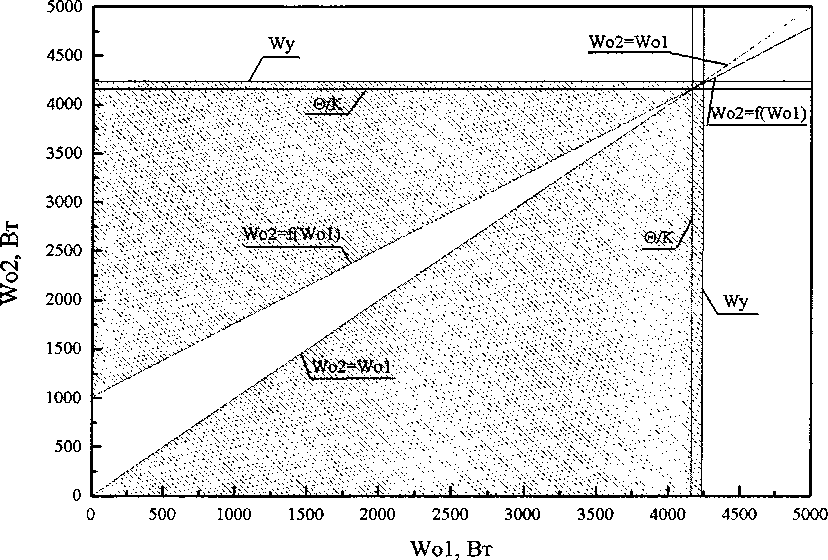
Список литературы Анализ возможности экономии тепловой энергии при прерывистом режиме отопления
- Панферов В.И. Моделирование и управление тепловым режимом зданий/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Материалы Международной науч. практической конф. «Теоретические основы теплогазоснабжения и вентиляции»: сб. М.: МГСУ, 2005. С. 94-98.
- Панферов В.И. Идентификация и управление тепловым режимом зданий/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Вестник ГОУ ВПО УГТУ-УПИ «Строительство и образование». 2005. № 14(66). С. 351-353.
- Панферов В.И. Математическая модель теплового режима зданий/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Энергетики и металлурги настоящему и будущему России: тез. докл. 5-й Всероссийской науч.-техн. конф. Магнитогорск: МГТУ, 2004. С. 23.
- Панферов В.И. Минимизация затрат энергии в процессе разогрева помещения при прерывистом отоплении/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Материалы Юбилейной XIV Международной науч.-техн. конф. «Достижения науки -агропромышленному производству»: сб. тр. Челябинск: ЧГАУ, 2006. Ч. 4. С. 165-168.
- Сканави А.Н. Отопление/А.Н. Сканави, Л.М. Махов. М.: Изд-во АСВ, 2002. 546 с.
- Табунщиков Ю.А. Минимизация расхода энергии, затрачиваемой на натоп помещения/Ю.А. Табунщиков, М.М. Бродач//Изв. вузов. Строительство и архитектура. 1988. № 12. С. 84-87.
- Табунщиков Ю.А. Экспериментальное исследование оптимального управления расходом энергии/Ю.А. Табунщиков, М.М. Бродач//АВОК. 2006. № 1. С. 32-36.
- Панферов В.И. Анализ экономичных способов нагрева металла в методических печах/В.И. Панферов, Б. Н Парсункин, Е.В. Торопов//Автоматическое управление металлургическими процессами: Межвузовский сб. науч. тр. Магнитогорск: МГМА им. Г.И. Носова, 1996. С. 63-72.
- Панферов В.И. О принципе экономичного управления нагревом металла и его реализации в методических печах/В.И. Панферов//Труды III Международной науч. практ. конф. «Металлургическая теплотехника: история, современное состояние, будущее. К столетию со дня рождения М.А. Глинкова. М.: МИСиС, 2006. С. 467-470.
- Теория автоматического управления: Нелинейные системы управления при случайных воздействиях: учеб. для вузов/А.В. Нетушил, А.В. Балтрушевич, В.В. Бурляев и др.; под ред. А.В. Нетушила. 2-е изд., перераб. и доп. М.: Высш. школа, 1983. 432 с.
- Растригин Л.А. Современные принципы управления сложными объектами. М.: Сов. Радио, 1980. 232 с.
- Панферов В.И. Оптимизация режима прерывистого отопления/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Проблемы теплоэнергетики: материалы Всероссийской науч.-техн. конф. студентов, аспирантов и молодых ученых. Челябинск: Изд-во ЮУрГУ, 2006. С. 31-32.
- СНиП 41-01-2003 «Отопление, вентиляция и кондиционирование». Госстрой России, 2004.
- Панферов В.И. Экономия тепловой энергии при различных режимах прерывистого отопления/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Энергетики и металлурги настоящему и будущему России: тез. докл. 7-й Всероссийской науч.-техн. конф. студентов, аспирантов и молодых ученых. Магнитогорск: МГТУ, 2006. С. 11-16.
- Панферов В.И. Оптимальный режим прерывистого отопления/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Материалы Пятой Российской науч. техн. конф. «Энергосбережение в городском хозяйстве, энергетике, промышленности». Ульяновск: УлГТУ, 2006. Т. 1. С. 161-165.
- Панферов В.И. Об оптимальном управлении тепловым режимом зданий/В.И. Панферов, А.Н. Нагорная, Е.Ю. Пашнина//Вестник ЮУрГУ. Серия «Энергетика». 2007. Вып. 8. № 20(92). С. 3-9.


