Анализ возможности перераспределения атомов углерода в решётке цементита

Цементит Fe 3 C является одной из основных фаз углеродистых сталей и чугунов. Он имеет орторомбическую решётку с параметрами a = 4,524; b = 5,088; c = 6,742 Å [1] и принадлежит к пространственной группе Pnma . В элементарную ячейку входят 12 атомов железа и 4 атома углерода. Положение атомов железа в решётке установлено надёжно, однако для атомов углерода рассматриваются два варианта размещения: в октаэдрических либо призматических порах железной подрешётки [2].

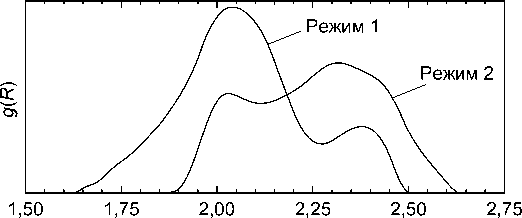
В последние годы появился ряд работ, в частности, Ю.В. Раца с сотрудниками [3, 4], в которых обнаружено заметное изменение ближайшего ок- ружения атомов в цементите при термообработке. На рис. 1 представлена функция радиального распределения атомов железа в ближайшем окружении атомов углерода (парная корреляционная функция – ПКФ C–Fe) в цементите стали У15, полученная в [4] на основе анализа спектров энергетических потерь электронов (метод EELFS) после двух вариантов термической обработки: 1) аустенитизация при 1050 °C и последующий перлитный распад при 500 °C в течение 1 мин (режим 1); 2) то же плюс дополнительный отжиг при 700 °C в течение 20 ч (режим 2). В обоих случаях наблюдаются два максимума, соответствующие ~2,0 и

R , Å

Рис. 1. Парная корреляционная функция C–Fe, полученная из анализа EELFS-спектров цементита в стали У15 после термообработки по режимам 1 и 2 по данным [4]

2,3…2,4 Å, однако после дополнительного отжига высота второго максимума сильно увеличивается.

В работах [5, 6] нами было показано, что в железной подрешётке цементита можно выделить поры четырёх типов: помимо упомянутых «нормальных» октаэдрических и призматических пор имеются также «искажённые» октаэдрические и призматические поры, и было высказано предположение, что наблюдаемые изменения ближайшего окружения атомов обусловлены переходом атомов углерода из «нормальных» призматических пор в поры иных типов. Целью данной работы является анализ возможности такого перераспределения атомов углерода в цементите.

В принципе, любые варианты расположения атомов углерода вне «нормальных» призматических пор должны повышать энергию цементита, так как радиус последних составляет 1,99…2,04 Å, что соответствует сумме атомных радиусов углерода и железа (0,77 + 1,24 = 2,01 Å [7]), а радиус пор прочих типов заметно меньше (см. таблицу). Однако перераспределение атомов углерода должно повышать и энтропию системы, поэтому состоянию равновесия (минимуму свободной энергии) должно соответствовать наличие какого-то количества атомов углерода в порах всех трёх типов. Поскольку длительный отжиг при 700 °C должен приводить систему в более равновесное состояние, то можно предположить, что именно такими переходами и объясняется наблюдаемое изменение ПКФ C–Fe.

Итак, в структуре цементита имеются четыре типа пор, причём количество пор каждого типа одинаково и втрое меньше числа атомов железа. Предположим, что в кристалле цементита, состоящем из 3N атомов железа и N атомов углерода, n1 атомов углерода перешло из «нормальных» призматических пор, где они первоначально располагались, в «нормальные» октаэдрические; n2 атомов углерода – в «искажённые» призматические и n3 атомов – в «искажённые» октаэдрические, тогда количество атомов углерода, оставшихся в «нормальных» призматических порах, равно n0=N-n1-n2-n3. (1)

Примем энергию исходного состояния за ноль ( ε 0 = 0) и обозначим энергию остальных трёх со-

стояний атомов углерода по отношению к исходному ε 1 , ε 2 и ε 3 ; будем приближённо считать, что взаимодействия между атомами углерода нет, то есть эти энергии остаются постоянными для любой конфигурации углеродной подрешётки. Тогда изменение энергии при переходе атомов составит

Δ E = n 1 ε 1 + n 2 ε 2 + n 3 ε 3 . (2)

Происходящее при этом изменение энтропии найдём с помощью формулы Больцмана

Δ S = k ln W , (3) где W – термодинамическая вероятность данного состояния системы, а k – постоянная Больцмана. Если ограничиться рассмотрением конфигурационной составляющей энтропии, то W равно числу способов размещения n 0 атомов углерода по N «нормальным» призматическим порам, n 1 атомов углерода – по N «нормальным» октаэдрическим

порам и т. д., а именно:

ли

W = ^{N !} ( N - n ₀)! n ₀!

N !

× ( N - n 1 )! n 1 !

N ! N !

×⋅ . ( N - n 2 )! n 2 !( N - n 3 )! n 3 !

Изменение свободной энергии системы при

перераспределении атомов углерода составит

Δ F =Δ E - T Δ S =Δ E - kT ln W .          (5)

Равновесию отвечает равенство нулю всех трёх частных производных свободной энергии:

∂Δ F ∂Δ F ∂Δ F ₀ ∂ n 1 ∂ n 2 ∂ n 3 .

Эти производные нетрудно найти, если учесть соотношение (1) и избавиться от факториалов в (4) с помощью формулы Стирлинга ln M ! ≈ M ln M - M .

Так, например,

∂Δ F ∂ n 1

- kT In [ NS.      1 = 0.

( n 1 N - n ₀ )

Если обозначить доли атомов углерода, занимающих соответствующие позиции, x_i = n_iN ( i = 0, 1, 2, 3) и ввести новые переменные

Атомы железа в ближайшем окружении (до 3 Å) атомов углерода, находящихся в порах различного типа [5, 6]

Тип поры Количество атомов и расстояния до них в Å Тип поры Количество атомов и расстояния до них в Å «Нормальная» призматическая (z =6) 2: 1,989 1: 1,992 1: 2,018 2: 2,039 2: 2,390 1: 2,836 «Нормальная» октаэдрическая (z =6) 2: 1,804 2: 1,858 2: 1,870 «Искажённая» призматическая (z =4) 2: 1,622 1: 1,624 1: 1,626 2: 2,516 «Искажённая» октаэдрическая (z =2) 2: 1,247 2: 2,270 2: 2,279 2: 2,981 yi = (1 - xi)/xi , то окончательно получаем следующую систему уравнений, описывающих равновесное распределение атомов углерода по порам всех четырёх типов:

г ; *               .8.

[ У 3 = У 0 /B3, где Bi = exp(-ei /kT). В таком случае условие x0 + x1 + x2 + x3 = 1 можно переписать в виде у 04 - У 0 (B- + B 2 + Вз + B- B2 + B2 B3 + B- Вз) -

• —2 у о ( B - B 2 + B 2 B 3 + B - B 3 + B - B 2 B 3) —

• - 3 B 1 B ₂ B ₃ = 0 .                              (9)

Решение этого уравнения позволяет найти величину y 0 , а затем при помощи соотношений (8) и остальные y _i и концентрации x _i .

Расчёт концентраций можно упростить, если учесть, что энергии ei вряд ли могут быть слишком малы, а рассматриваемые температуры не превышают 1000 К. По этой причине коэффициенты Bi должны быть существенно меньше единицы и их двойными и тройными произведениями в (9) можно пренебречь. Тогда равновесные значения yi » ^B1 + B2 + B3 /Bi , то есть x =------ Bi         •.                      (10)

B i + Bb_x + B ₂ + B ₃

Поскольку сам вопрос о том, в каких позициях железной подрешётки цементита размещаются атомы углерода до сих пор не имеет окончательного ответа, то прямых экспериментальных измерений энергии соответствующих состояний, разумеется, нет. Однако в последние годы появились работы, где энергии кристаллической решётки цементита были рассчитаны «из первых принципов». В первой работе такого рода [8] было найдено, что при размещении всех атомов углерода в «нормальных» призматических позициях энергия когезии (энергия, выделяющаяся при образовании кристаллической решётки из изолированных атомов, взятая с обратным знаком) цементита Fe3C составляет 7,33 эВ/атом, а при их размеще- нии в «нормальных» октаэдрических позициях – 7,16 эВ/атом. Следовательно, если принять за нулевой уровень энергию атома углерода в «нормальной» призматической поре (e0 = 0), то его энергия в «нормальной» октаэдрической будет составлять е1 =-(7,16 - 7,33)/xCe3C = 0,68 эВ; здесь xCe3C = 0,25 - атомная доля углерода в цементите. В более поздней работе [9] была получена разность энергий решётки цементита с размещением атомов углерода в «нормальных» октаэдрических и призматических порах 0,068 эВ/атом, откуда е1 =-0,068/xCe3C = 0,272 эВ.

Расчёты энергии атома углерода в «искажённых» призматических и октаэдрических порах в [8, 9] не делались, поэтому попытаемся получить приближённую оценку на основании имеющихся результатов. Будем считать, что энергия атома углерода пропорциональна числу атомов железа в первой координационной сфере, а зависимость этой энергии от радиуса первой координационной сферы в неискажённой решётке линейна. Согласно таблице для «нормальных» призматических и октаэдрических пор число таких атомов железа z = 6, а расстояния до них составляют R i = 1,99^2,04 и 1,80^1,87 А соответственно. Среднее расстояние составляет для «нормальных» призматических позиций ^z

R 0 = - ' Е R = 7' 12,066 = 2,011 А, (11) ^z t = 1        ⁶

а для «нормальных» октаэдрических –

z

R 1 = -• Е R i= - ' 11,064 = 1,844 А. (12) ^z i = 1        ⁶

«Искажённую» призматическую пору окружают z = 4 атома железа на расстояниях R i = 1,62^1,63 А, поэтому для неё

z

R ₂ = - /Е R. = -' 6,494 = 1,624 А. (13) ^z i = 1        4

Наконец, в первой координационной сфере «искажённой» октаэдрической поры располагаются всего z = 2 атома железа на очень малом расстоянии R i = 1,247 А, так что

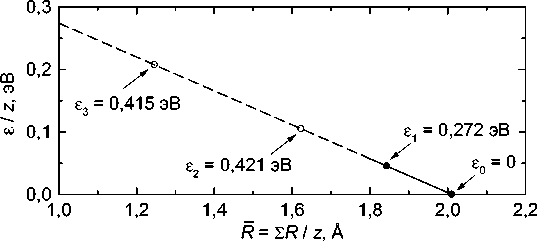
Рис. 2. Зависимость энергии атома углерода в решётке цементита е , отнесённой к числу атомов железа в первой координационной сфере z , от радиуса первой координационной сферы R

z

R = - .£ R = - - 2,494 = 1,247 A. (14) z 1 = 1       2

На рис. 2 представлена зависимость энергии этих состояний в расчёте на один атом железа в первой координационной сфере от среднего радиуса этой сферы R . Прямая, проходящая через значения для «нормальных» призматических и октаэдрических позиций, описывается уравнением e/z : 0,5459-0,2715- R , эВ.(15)

Это даёт для энергии атома углерода в «искажённой» призматической поре оценку e2 /z = 0,105 эВ, откуда e2 = 0,421 эВ,(16)

а в «искажённой» октаэдрической e₃ / z = 0,207 эВ и

Е3 = 0,415 эВ.(17)

Отметим, что значения энергий для «искажённых» пор обоих типов оказались очень близки и не слишком значительно превышают значение для «нормальных» октаэдрических пор.

При указанных значениях энергий коэффициенты B , при 700 °C будут равны B 1 = 0,0390; B ₂ = 0,0066; B ₃ = 0,0071, а концентрации

% ! : 0,145; x ₂ : 0,028; x ₃ = 0,030.       (18)

Очевидно, что столь малые количества атомов углерода в порах разных типов не могут вызвать наблюдавшиеся изменения EELFS-спектров (см. рис. 1). Конечно, приведённые оценки являются очень приблизительными, так как действительные значения энергий е2 и Е3 могут быть иными.

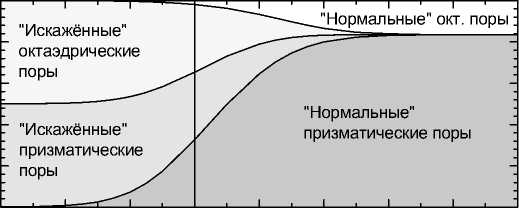
Поэтому будем считать эти энергии свободными параметрами и попытаемся оценить, как их значения будут влиять на степень заполнения пор разных типов. На рис. 3 приведены значения концентраций x i , рассчитанных по формулам (9) и (8) при условии, что Е 1 : 0,272 эВ и e ₂ =e ₃ . Как видно, доля атомов углерода, находящихся в «искажённых» порах, становится заметной при значениях е ₂ и е ₃ менее ~0,3 эВ.

Вернёмся к результатам [4] (см. рис. 1). Фактически после обоих режимов обработки у ПКФ наблюдались два пика – при ~2,0 и 2,3…2,4 Å. Как видно из таблицы, атомы железа могут находиться на таком расстоянии от атома углерода при различных вариантах расположения последнего. Поскольку пиков на расстояниях меньших чем 2 Å не наблюдается, то можно предположить, что даже при размещении атома углерода в «тесных» порах он смещает окружающие атомы железа, так что они оказываются от него на расстоянии, близком к 2 Å (которое, как было отмечено выше, равно сумме атомных радиусов углерода и железа). В работе [10] показано, что как бы ни было мало расстояние между атомами в

ч- 1.0 го

§ 0,8 о_

(D

Е 0,6

О 0,4

О fe 0,2

и;

§ 0,0

d -0,6   -0,4   -0,2   0,0    0,2    0,4    0,6    0,8    1,0

• ^e 2 = £ з ^, эВ

  Рис. 3. Зависимость доли атомов углерода в порах каждого из четырёх типов от избыточной энергии атомов углерода в

  «искажённых» призматических и октаэдрических порах ²³

  

  ^Е2 = ^Eз^{, эВ}

  
  

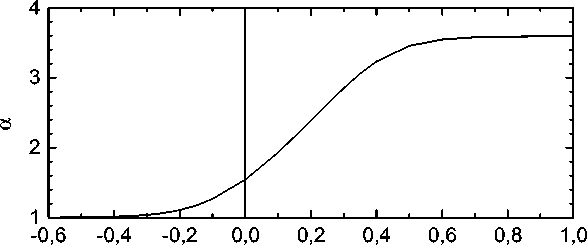
Рис. 4. Зависимость отношения высот первого и второго максимума ПКФ C–Fe от избыточной энергии атомов углерода в «искажённых» призматических и октаэдрических порах 23

решётке железа при помещении между ними атома углерода расстояние C–Fe всегда оказывается не менее 1,75…1,90 Å.

Если считать, что смещаются атомы только первой координационной сферы, то на основании данных таблицы можно записать, что отношение интенсивностей первого и второго пиков ПКФ

6 x 0 + 6 x 1 + 4 x 2 + 2 x 3 3 - x 2 - 2 x 3

2 x 0 + 2 x 2 + 4 x ₃      1 - x 1 + x ₃

На рис. 4 приведены значения этого отношения, рассчитанные на основании данных рис. 3. Из рис. 4 следует, что при любых значениях e2 = e3 > 0 первый пик должен быть минимум в полтора раза выше второго.

В то же время можно заметить, что некоторые первопринципные расчёты [11] указывают на весьма малые значения энергии образования вакансии в углеродной подрешётке цементита (~0,2 эВ). Это указывает, во-первых, на то, что и другие искажения углеродной подрешётки могут приводить лишь к небольшим изменениям энергии кристалла Fe3C, а во-вторых, что при приближении к равновесию в процессе отжига цементит может терять часть атомов углерода из пор разных типов, что скажется на ближайшем окружении оставшихся атомов. Поэтому для ответа на вопрос о возможности возникновения разных конфигураций углеродной подрешётки требуются прямые расчёты энергий соответствующих состояний цементита.

Работа выполнена в рамках ФЦП «Научные и научно-педагогические кадры инновационной России».