Анализ возможности применения некоторых численных методов для решения задач механики многокомпонентных сред

В связи с развитием современной вычислительной техники резко возросла роль математического моделирования физических процессов, используемых в науке и технике. Более того, есть такие проблемы, когда математическое моделирование является единственным средством предварительного изучения явлений. Поэтому с особой остротой встает проблема адекватности математических моделей тем физическим процессам, которые они пытаются описывать. В природе практически нет чистых веществ, поэтому активно развиваются математические модели многокомпонентных сред [1]. Для верификации расчетов, с одной стороны, используют известные экспериментальные данные, а с другой стороны, при анализе проведенных измерений используют математические модели. Очень важно, чтобы условия проведения расчетов и экспериментов совпадали, а математическая модель была адекватна изучаемому физическому процессу.

Перспективное использование взрывных процессов в ряде отраслей современной техники тесно связано с решением вопросов обеспечения мер безопасности, защиты инженерных сооружений и технологического оборудования от действия ударных волн (УВ). В связи с этим важное прикладное значение представляет изучение проблемы локализации механических эффектов взрыва и ослабление УВ.

В настоящее время на практике ослабление УВ в газе осуществляется путем применения различных экранирующих систем в виде сплошных, перфорированных и разрушающихся перемычек. Один из основных недостатков сплошных и перфорированных перемычек состоит в их весьма большой материалоемкости и соответственно большой величине объемного содержания α твердого конденсированного вещества ( α ≈ 1÷0,1). Указанный недостаток в меньшей степени относится к перемычкам, разрушающимся при взаимодействии с УВ и образующим экранирующие слои или завесы из пены или аэровзвесей.

В последних работах, посвященных исследованию закономерностей ослабления УВ слоями аэровзвесей, для снижения давлений и импульсов УВ предлагается и обсуждается использование «каркасных систем», представляющих собой систему мелкоячеистых решеток.

В настоящей статье на примере анализа математической модели аэровзвеси [2] на инвариантность относительно преобразования Галилея [3] оценим правомерность применения метода крупных частиц при решении данных задач.

Работа выполнена при поддержке РФФИ грант № 13–01–00072.

1. Постановка задачи и математическая модель

Рассмотрим математическую модель течения газа с твердыми частицами (аэровзвесь), которая описывается системой уравнений [2], и оценим адекватность результатов, полученных в эксперименте и в расчетах, проведенных методом крупных частиц.

Система уравнений движения аэровзвеси [2] имеет следующий вид:

^d P i ₊dp v i _— J d t     d x

dp 2 dp 2 V 2 _

1— - J ;

5t     5x

5 n 5 nv₂

— +---2 — 0;

5 t    5x spivi sp!v2     ap_

--1---Г Ui --- — — f + JV ^ ;

a t      a x       a x

ap 2 ^v 2 ap 2 ^v 2 3    a p

--1---1 a^   — f — JV') ;

a t a x    2    a x

dp ₂ e ₂ dp ₂ e ₂ v ₂ a t        a x

f q ,     T 2 <  T s

I— Je 2 , T 2 >  T s ;

^{d(p i} E + ^p 2 E 2 ) +A^p i ^v i E i + p 2 ^v 2 E 2 ₊( ^a i ^v i + ^a 2 ^v 2 ) p j = ₀; at         ax^{L                                  J}

e i ^— c p ^{( T}i ^— T o )^— p "^ ’ p i

e 2 ^— c 2 ⁽ T 2 ^— T o ) ⁺ Q ^— "v ^; p 2

P —

° pi RiTi . ;

i — Ppi

p i — p i ° a i ;

p 2 —p ₂ a ₂;

p ₂ — const;

q — n n d X _iNu ( T_i — T ₂ ) ;

/ ^— n л d ²p ° ^C _d ( ^v i ^{— v} ₂ )| ^v i ^{— v} 21/8 ;

E — e + v^ . ii 2

°

Здесь индексы i, 2 относятся соответственно к газу и частицам; p i , a i ( i = l, 2) - истинные плот

ности и объемные содержания фаз; p i , v i , T_i , e i , E i - средние плотности, скорости, температуры, внутренние и полные энергии фаз; Q ° - теплота химической реакции при T ₂ — T o , p — p 0 ; р - давление; п - число частиц в единице объема смеси; р - ковольюм; c_p и c 2 - теплоемкости

фаз; X _i - теплопроводность газовой фазы; R_x - газовая постоянная; C_d и Nu - коэффициент трения и число Нуссельта, определяемые числами Рейнольдса (Re) и Прандтля (Pr) относительного движения; d - диаметр частиц; u_s и ф - эмпирические константы, характеризующие скорость горения топлива. Уравнения (1)–(3) – уравнения неразрывности газа и частиц и уравнение сохранения числа частиц в единице объема смеси; (4)–(5) – уравнения импульса газа и частиц; (6)–(9) – уравнения энергии частиц и смеси в целом; (10)–(14) – уравнения состояния; (15) – уравнения, определяющие члены массового ( J ), теплового ( q ) и силового ( f ) взаимодействия между фазами.

2. Анализ инвариантности относительно преобразования Галилея уравнений движения аэровзвесей

Запишем исходную систему уравнений в новой системе координат, движущейся с постоянной скоростью D . Скорости в новой системе координат будут равны:

V 1h = v + D ;                                                                            (17)

v 2h = ^v 2 ⁺ D .

Координата будет определяться из уравнения x„ = x + Dt .

н

Производные:

d d dx  dxн

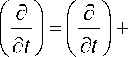
< л A

T-l D

(^{d x} н )

Таким образом, уравнение (1) с учетом (16)–(20) принимает вид:

dPi +dPi D । dpi (vih - D)—J 5t   5xH         5x H или dpi+d£i D+dPiViH dPiD — J dt   dxH      dx H

Получаем dpi, dPi viH — J dtd

Аналогично, уравнения (2) и (3) с учетом (16)–(20) принимают вид:

dP2 dP2v2h _, .

--1--— — J ;

d t

dn , d nv 2h — 0 dtd

Запишем уравнение (4) в новой системе координат:

^dP i ⁽ v iH ^— D ) , ^dP i ⁽ v iH ^— D) _n , ^d P i ⁽ v iH ^— D ) 2 , _n ^dP _ f

1D ++ a—— dt           dxH              dxH

или

5p i v iH 5p i D 5p i v iH D 5p i D ² 5p i v i;     5p i v iH D 5p i D ²       5 p

1121г ai dt      dt      dx H      dxH     dxH       dx H      dxH      dx H

Используя (22), получаем

^dP i v iH d t

dp _i v _i ² _H        d p      „ _T

⁺  ---⁺ “i л--^— - ^{f + J} v 2h .

dxH      dxH нн

Аналогично получается уравнение (5) с учетом (21):

^dP 2 ^v 2h d t

₊ dP 2 V 2H 5 x н

+—a

d p

^{2 d x} H

^— f ^{— Jv} 2h -

Рассмотрим уравнение (6):

dp2e2 + dp2e2 D + dp2e2 (v2h — D) f q,    T2 < Ts dt     dx„            dx„         I — Je2, T2 ^ T ’ нн    s или dp2e2 dp2e2 ^ dp2e2V2H dp2e2D J q, T2 < T

+^7"D+^7---dx- = 1— Je, T > I/ н   нн     s

Откуда получаем dp2e2 +dp2e2V2H = f q,    T2 < Ts

dt

d x н

— Je 2 , T 2 ^ T s

.

Рассмотрим уравнение энергии (7), учитывая (16),

5 pi ei +

( v iH

—

D2 J

к

к

+ p ₂ e ₂ + к

( v 2h

—

DL

7 d t

5 pi ei +

+к

к

( v iH

—

D2 J

+ p ₂ e ₂ + к

( v 2H

—

DL

d x н

----^7e D +

⁺T^d- ^p i ⁽ v iH ^{— D} ) e i ⁺ d x

( viH — D )2

_             к

Раскрывая скобки, получаем

'

^{+ p} 2 ^{( V} 2h ^{— D} ) ^e 2 ⁺ к

^{( V} 2h ^{— D ) 2}

^{+ (a} i ^{( v} iH ^{— D ) + a} 2 ^{( v} 2H ^—

dp i e i + dp i ( v iH

dt

—

2d t

^D ) 2 + dp 2 e 2 d t

+ dp 2 ( v 2h — D ) 2 + dp i e i D + dp i D ( v iH — D ) ² +

2d t

d x н

d x н

+ dp 2 e 2 D + ^дР 2 D ( v 2h

—

—

d x н

dpiD (viH —

^2d X н

d x н

^D ) 2 + ^dP 2 e 2 v 2h

^D ) 2 + dp i e i v iH + dp i v iH ( v iH

d x н

—

d^p ₂ D(v ₂H-

2dXн

d x н

D )2 + daip (viH — dxн

+ ^dP 2 v 2h ( v 2h

2dXн

—

—

D ) 2 dp _i e _i D

^{2d x} H

D ) 2 dp ₂ e ₂ D d x н

^D ) ^da 2 p ( v 2h ^{— D} )

1= 0. d x н

После алгебраических преобразований получаем

r

dp i e i ⁺ v i^

⁷ + d t

r

dp2 e2 + v2H к 2 7 dt

—

—

—D

' dp i v iH + dp i v iH

к d t

d x н

dp

^{+ a}i^ d x н J

d x н

+ D 2 'sp , + ap i v i, J+ D 2 ra^p₁+

—D

_к d t

dp ₂ v ₂ H

к

dt

dx н 7

+ dp2V2H

_к d t

dp 2 v 2h d x н

—

D   dp

+--On--+

2 ² d x н

v 2 I dp i v iH e i ⁺ Чт

к

7 +

dp 2 v 2h ^e 2 к

d x н

„2 I

+i1

2 7

3     d p

+ ?a2T^

^{2   d} x н J

+

+ dp i D ( v iH ^—

2dXн

d x н

D ) 2 + dp 2 D ( v 2h — ^2d x н

d x н

D ²

—= = 0.

d V i_H

+ a, —— + a к   dx H

d V 2h I

2--2H I p +

Ay I dx н 7

Согласно (22) и (23) сумма третьего и четвертого слагаемых обращается в ноль, а пятое и шестое слагаемые согласно (25) и (26) будут равны ( Df - DJv _2н) и ( — Df + DJv _2н). В результате получим

^d ( p i ^E ,h +p 2 ^E 2h )

d t

d

⁺ ^[p i v iH E iH +p 2 ^v 2h E 2h ⁺ ( ^a i ^v i ^+a 2 ^v 2 ) P ] ⁺ d x

, D„, d p , dp i D ( v iH + a^    +

2 ² d x _H        2 d x _H

—

D )2 dp2 D ( v 2h — D )2

.

^{2d x} H

Заключение

1. Анализ инвариантности законов сохранения аэровзвесей [2] относительно преобразования Галилея при переходе в подвижную систему координат уравнения неразрывности газа и частиц

• (22)    и (23), уравнение сохранения числа частиц в единице объема смеси – (24) и уравнения движения аэровзвесей (25) и (26) являются инвариантными относительно преобразования Галилея.

• 2.    Уравнение полной энергии смеси в новой системе координат принимает вид (28), в нем появляются дополнительные слагаемые, что говорит о нарушении инвариантности относительно преобразований Галилея.

• 3.    Применение метода «крупных частиц» является не правомерным для расчета течений аэровзвесей [2], так как использует неинвариантное относительно преобразований Галилея уравнение полной энергии смеси, а результаты расчетов не могут быть признаны достоверными.

Авторы выражают свою благодарность профессору В.Ф. Куропатенко за полезные обсуждения и интерес к работе.