Анализ времени ожидания в G/G/1 очереди

В телекоммуникационном оборудовании аналитическое исследование и расчет статистических параметров трафика дает возможность приблизиться к определению пропускной способности сети, оптимального размера буфера. Для решения задач, в которых существуют случайные события, используются как аналитические, так и имитационные модели. Зачастую аналитические модели предпочтительнее имитационных по нескольким причинам: не требуется проведения большого числа испытаний; можно получить оптимальное решение.

Традиционная теория очередей посвящена очередям, где время между прибытием и время обслуживания являются независимыми процес- сами обновления. Есть предположение о том, что длительности обслуживания пакетов взаимно независимы, а допущение о независимости потока пакетов от интервалов между прибытиями неоправданно – следовательно, необходимо учитывать при моделировании СМО G/G/1 свойство самоподобия данных процессов. Изучение очередей с зависимыми процессами прибытия является актуальным и имеет практическую ценность. Можно сделать вывод: точные решения (аналитические или численные) обычно недоступны для очереди G/G/1, так как исследователи прибегают к моделированию Монте-Карло или используют классическую теорию Маркова и ее вариации для проведения параметрического анализа по средней длине очереди [1].

Корреляции в прибывающем потоке событий, в предположении очереди на один сервер, существенно влияют на среднее время ожидания по сравнению с соответствующим потоком событий, приходящих повторно, тому же серверу. Однако если использовать такие модели СМО G/G/1, для которых созданы и построены реальные или максимально приближенные к действительности аппроксимации распределений интервалов времени между пакетами и длительности обслуживания для очередей с коррелированными поступлениями [2], становится возможным поиск решения неизвестных средних характеристик трафика. В основном используются распределения с «тяжелым» хвостом Парето и Вейбулла для построения процесса прибывающего потока пакетов и определения среднего времени ожидания пакета в очереди, учитывая его скорость, коэффициент вариации и другие характеристики.

Исследование, проведенное относительно распределения времени между пакетами, описываемых распределениями с «тяжелым» хвостом Вейбулла, Парето показало, что его можно использовать для аналитического определения параметров трафика [3-4]. Применение распределений с «тяжелым» хвостом наилучшим образом приближено к функциям распределений, описывающих статистические характеристики трафика. Определяя преобразования Лапласа законов распределений, которым подчиняются интервалы времени между пакетами и длительности пакетов, и используя спектральный метод решения интегрального уравнения (ИУ) Линдли, можно найти функцию времени ожидания пакетов в очереди. Определение данной сетевой характеристики позволяет повысить качество обслуживания при конфигурации сети и проследить изменчивый характер трафика, учесть его свойства, чтобы, в свою очередь, наиболее точно оценить параметры сети.

Предложенный в [5] метод аппроксимации распределения суммой затухающих экспонент дает неудовлетворительные результаты по точности на «восходящих» ветвях распределений. Кроме того, аппроксимация «восходящих» ветвей распределений приводит к появлению в сумме затухающих экспонент слагаемых с отрицательными коэффициентами, что нивелирует вычислительные преимущества спектрального метода, обусловленные использованием гиперэкспоненциальных распределений.

Анализ времени ожидания в очередях СМО G/G/1 с использованием приближения PMRQ аппроксимации

Ряд исследований подтвердили теоретические расчеты, продемонстрировав влияние автокорреляций в процессах прибытия (или сервисных процессах) на статистику очередей в связанных очередях по сравнению с их аналогами обновления [1; 5-6]. В более общем случае, если данные о статистических параметрах доступны, то методы, рассмотренные и проанализированные в этом исследовании, могут быть использованы для получения среднего времени ожидания. Для исследования произвели анализ результатов, полученных в работе [7]. Идея данной работы заключается в сравнении результатов аппроксимации способами PMRQ и PMRS при сопоставлении СМО G/G/1 аппроксимирующей GI/G/1 [7] и аппроксимации суммой затухающих экспонент [5,6] при одних и тех же параметрах сети, смоделированными и приближенными к реальным значениям.

Предложенная схема аппроксимации, представленная в работе [7], которая сопоставляет G/G/1 аппроксимирующей GI/G/1 PMRQ (Peakedness Matched Renewal Queue) использует аппроксимации потока распределения услуг в пиковом режиме, которые имеют названия PMRS (Peakedness Matched Renewal Stream). Приближенный процесс прибытия PMRS сохраняет пиковость исходного процесса прибытия и его скорость прибытия; кроме того, квадратный коэффициент вариации построенного процесса прибытия PMRS равен индексу дисперсии исходного процесса прибытия. Заслуга приближения PMRQ заключается в том, что он легко разрешим, в отличие от первоначальной очереди G/G/1. Для этого в [7] используется функция меры остроты пика [8], а отставание учитывается коэффициентом автокорреляции в исходном потоке.

Приближение PMRQ аппроксимации способом для поиска среднего времени ожидания в схеме TES+/G/1 (Transform Expand Sample) лучше по сравнению со ссылочными значениями, полученными с помощью моделирования, где простой вариант процессов прибытия TES+ служил процессом прибытия, связанным с автокором [9-10]. Универсальные классы автокорреляционных (лопастных) стохастических процессов, называемых TES+ [9-10], впоследствии служат процессами прибытия в очереди G/G/1, результирующая TES+/G/1 – это проверка эффективности среднего времени ожидания приближения, предложенного в [7]. При рассмотрении данной мо- дели одновременно подбираются маргинальное распределение и корреляционная функция.

Целью при аппроксимации PMRQ и PMRS является построение модели, соответствующей трем требованиям одновременно: маргинальное распределение должно соответствовать ее оригиналу (гистограмме); основные корреляционные модели должны приближаться к оригиналам до приемлемой задержки; выборки, сгенерированные моделью, должны «иметь сходство» с опытными временными сериями.

Интересное приближение PMRS возможно следующим образом. Можно показать [8], что пиковая функция любого возобновляемого потока трафика R имеет представление zR(s)=            R , s>0,        (1)

l-aR(s) s где aR(s) – преобразование Лапласа плотности временного интервала между временем и XR. Из (1) следует, что для общего движения процесса X соответствующее PMRS аппроксимирующего процесс обновления p полностью определяется через преобразование Лапласа от его плотности временного интервала между временем вида aR (5) = 1--Ц——, 5 > 0.       (2)

Z_v(5) + X_x / S

Уравнение (2) фактически подразумевает, что X_R = X _v. Обоснование аппроксимации PMRS очевидно: в целом R аналитически проще, чем X – факт, который будет использоваться позже в приблизительном анализе очереди G/G/1. Более конкретно, PMRQ аппроксимации очереди G/G/1 общего процесса X является просто соответствующей очереди GI/G/1 с обновлением предлагаемого трафику процесс R , где R – PMRS аппроксимации X . Поэтому трафик рассматривается как пульсирующий процесс времени [11], имеющий описания и свойства процессов TES [9].

Процессы TES представляют собой универсальный класс стационарных временных рядов, допускающих любое предельное распределение, большое разнообразие автокорреляционных функций (монотонность, колебание, чередование и др.), и широкий спектр поведения, в том числе направленных и ненаправленных процессов. Процессы TES могут быть разработаны, чтобы соответствовать любому эмпирическому (маргинальному) распределению, и, одновременно, приближенным эмпирическим автокорреляционным функциям различных функциональных форм. В частности, можно определить TES процессы с различными автокорреляционными функциями, тем самым контролируя (оценивая) их степень.

Решение статистики равновесного времени ожидания в очереди GI/G/1 обычно требует сложной расчетной процедуры. Для нахождения функции времени ожидания W(y) (3) необходимо воспользоваться обратным преобразованием Лапласа функции Г($) посредством интегрирования, учитывая, свойства дельта-функции [1] (например, ИУ Линдли для частного случая)

^ (.v) = j w(T)d t.               (3)

Для оценки параметров приближенного среднего времени ожидания в качестве альтернативы вычислению среднего времени ожидания рассматривается приближение большого трафика. Из работы [7], когда GI/G/1 имеем очередь при большом трафике, а именно p —> 1 , аппроксимация среднего времени ожидания (4)

_ 5[У1(с2¥+сЛ p w» L л Y           ,          (4)

2      1-p где c Y, cy – коэффициенты вариации интервалов поступления времени X и времени обслуживания Y соответственно [12].

В [7] исследована эффективность предлагаемого приближения путем сравнения с моделированием. Проведено сравнение точности аппроксимации W двумя способами: масштабный метод усреднения и аппроксимация W , изменялись три типа параметров W в системе TES+/G/1. Рассмотрены частоты поступления со значениями X = 0,6 и X-0,8. Данные частоты соответствуют средней загрузке и тяжелой загрузке системы соответственно, поскольку среднее значение службы всегда было равным единице. Параметр пачечности ^E должен быть различен по диапазону значений надлежащим выбором параметров LhR. Значения LhR определяют сильный эффект пачечности, в то время как X имеет вторичный эффект. В результате рассмотрены среднесрочные распределения времени обслуживания: Exponential, Erlang, Deterministic, MCE2 и MMPP (Markov-modulated Poisson processes) [7], где получены результаты для среднего времени ожидания СМО TES+/G/1.

Аппроксимация в виде суммы затухающих экспонент

Анализ сетевого трафика проводился с использованием сети связи, в которой при передаче в гло- бальную сеть через коммутатор были получены данные, имеющие один Uplink. Пропускная способность абонентского канала изменялась с помощью программного обеспечения коммутатора, а порт, являющийся пограничным для этого коммутатора, имел конфигурацию зеркалирования, что позволяло производить захват всего трафика, проходящего в глобальную сеть. Uplink к узлу агрегации был занижен по скорости, а именно скорость передачи была ограничена до 60 и 80 Мбит/с.

Основываясь на имеющихся исследованиях трафика при загрузках со значениями £ = 0,6 и Х = 0,8, и полученных распределений согласно их гистограмме, были рассмотрены случаи системы СМО G/G/1: система типа P/W/1 и W/P/1, где символы P и W означают соответственно распределения Парето и Вейбулла. Распределение Парето и Вейбулла, соответственно, имеют вид:

№ =

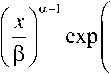
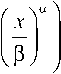
где a – параметр формы; P – масштабный параметр. Уравнение Линдли имеет следующий общий вид [1]:

F(x) = |Я(х - yW(y'), 0

где F(*) – функция распределения времени ожидания требования в очереди; H^ – ядро, связывающее произвольную функцию распределения вероятностей интервалов времени между поступлениями соседних требований Л(т) и произвольную функцию распределения длительности обслуживания требований 5(t) . Заметим, что само ИУ Линдли выведено в предположении независимости элементов последовательности интервалов времени между заявками и интервалов времени обработки заявок.

Известно, что для СМО G/G/1 возможен спектральный метод решения ИУ Линдли, если для плотностей вероятностей <7(т) И b(F) , соответствующих распределениям Л(т) и S(t) , использовать аппроксимацию в виде суммы затухающих экспонент [3-4]. При этом «М и 6(t) имеют представления, соответственно:

a^ = ^_ke"^\ (8)

МА^/1’^

где n = 5; / - 5 . Среднее время ожидания пакета в очереди для вышеприведенных примеров находится согласно известному свойству характеристической функции dF^

cp ds

5 = 0

По результатам моделирования была проведена проверка соответствия параметров генерируемого узлом-отправителем потока заданным параметрам с использованием программы EasyFit. Рассматривался случай с частотой поступления или интенсивностью £ = 0,6. Данная частота соответствуют средней загрузке системы, соответственно, поскольку среднее значение интенсивности обслуживания всегда равно единице. При рассмотрении СМО TES+/G/1 (распределение интервалов времени между поступления TES+ и длительностей обслуживания MGE2) с параметрами: X = 0,6; £ = 0,05; 7? = 0,05; A_E =27,181; p^(l) = 0,6915; ц = 1. После вычисления по масштабному методу усреднения и аппроксимации W среднее время ожидания пакета получилось равным t_cp=^-

Если рассмотреть при той же средней загрузке £ = 0,6 полученные гистограммы статистических параметров снятого трафика (см. рисунок 1), имеем соответствие системе W/P/1. Интервалы времени между пакетами распределены по закону Вейбулласпараметрами: a, =0,13; p, =0,000225, а для длин пакетов распределением Парето с параметрами a = 0,39; p = 54. После аппроксимации распределений СМО W/P/1 в виде суммы затухающих экспонент для поиска решения ИУ Линдли среднее время ожидания пакета получилось равным£„-42.6.

Рассмотрен случай при пиковой загрузке системы при интенсивности 2 = 0,8 СМО TES+/G/1 (MMPP (Markov-modulated Poisson processes)) [7], где получены результаты для среднего времени ожидания. СМО MMPP с параметрами: £„=0,8; ^ = 1; _g = [0,96;0,04]; p = 0,8. После вычисления по масш т абному методу усреднения и аппроксимации W mmpp (7) среднее время ожидания пакета получилось равным t_cp= 62,29. Далее

W MMPP — — p

—---- X [2p + Xyn, - 2m_x ((1 - p)g

2(1 -P)

+/я₁ПЛ)(5 + ell) ¹ X] — -^X_om_:

где е -вектор 2x1 от l's ; Х = (Х,,Х2); р = Х;

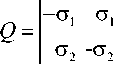
X, О

О X,

п =

°2

^о, + а.

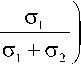
находятся из алгоритма

[13]. Если рассмотреть при том же значении за- грузки Х = 0,8 полученные гистограммы стати- стических параметров снятого трафика (рис.1), имеем соответствие системе W/P/1. Интервалы времени между пакетами распределены по закону Вейбулла с параметрами: ср =0,78; р1 =1500, а для длин пакетов распределением Парето с параметры: а = 0,41; р = 62. После аппроксимации распределений СМО W/P/1 в виде суммы затухающих экспонент для поиска решения ИУ Линдли среднее время ожидания пакета получилось равным tcp =50,662.

Заключение

В статье представлены методики определения среднего времени ожидания в очереди СМО G/G/1: масштабный метод усреднения и аппроксимации W , а также аппроксимация в виде суммы затухающих экспонент для поиска решения ИУ Линдли. При этом в качестве модуля транспортного уровня выбран модуль TCP, а интенсивность поступления пакетов равна X = 0,6 и X = 0,8.

Погрешность решения ИУ Линдли спектральным методом в сравнении с результатами [7] составляет при Х = 0,6 порядка 4%, а при Х = 0,8 – до 14%, что вполне приемлемо. Такая погрешность может быть связана с идеализацией исходных распределений временных параметров рассматриваемых моделей, с допущением независимости элементов рассматриваемых последовательностей интервалов времени и с определенными точностями, характерными для любой используемой программы при снятии и обработке сетевого трафика.

Захват трафика осуществлялся с помощью программы анализатора трафика Wireshark. Распределения временных параметров были получены в программе анализа данных EasyFit, разработанной для быстрого анализа статистических данных и принятия решения. Проведенное сравнение методов аппроксимации сетевого трафика позволяет оценить среднее время ожидание пакета с использованием статистического анализа данных, что даст возможность повысить качество обслуживания и спрогнозировать поведение трафика.