Анализ взаимозависимостей геометрических параметров эксцентрикового механизма качения

Актуальность. Повышение эффективности технологических операций по перемешиванию или смешиванию различных веществ является актуальной задачей, решение которой возможно обеспечить посред-ствам использования механизмов со сложным движением выходного звена. К механизмам данного вида относится эксцентриковый механизм качения (ЭМК), который состоит из двух колец и тел качения с радиусами различной величины [1]. Вид воспроизводимого движения рабочего органа определяется законом движения выходного звена механизма провода технологического оборудования, точность реализации которого завит сочетания величин показателей качества механизма привода. Основными параметрами механизма, формирующими значения показателей качества, являются геометрические параметры. Анализ взаимозависимо-стей геометрических параметров ЭМК позволит получить предпосылки для дальнейших теоретических исследований, а также сформировать ряд рекомендаций по выбору их величин для каждого вида структурной схемы механизма.

Цель – анализ взаимозависимостей геометрических параметров ЭМК.

Задачи : формирование диаграммы изменения угла подъема эксцентрика ЭМК; формирование диаграммы изменения радиусов от угла положения тел качения ЭМК; анализ взаимозависимостей геометрических параметров ЭМК по полученным диаграммам.

Эксцентриковый механизм качения в зависимости от расположения тел качения относительно осей симметрии может быть реализован одним из вариантов структурных симметричных схем (рис. 1), каждая из которых реализуется совокупностью двух колец и тел качения с радиусами разной величины при наличии или отсутствии зазора между этими звеньями [1].

С целью повышения эффективности теоретических исследований эксцентрикового механизма качения, авторами разработан программный комплекс (ПК) «Эксцентрик» [2]. Используя программное обеспечение, выполнено решение задачи по определению геометрических параметров для каждой схемы ЭМК по двум направлениям ввода поправки в расчет, а также при наличии и отсутствии зазора между телами качения при R 2 = 60 мм, R 1 = 40 мм, e = 4 мм и с = 5 мм, где R 2 , R 1 , e и с – радиусы дорожек качения наружного и внутреннего колец, эксцентриситет и зазор между телами качения. Выбор величин исходных данных осуществлен из областей существования механизма-прототипа ЭМК, сформированных в соответствии с работой [3].

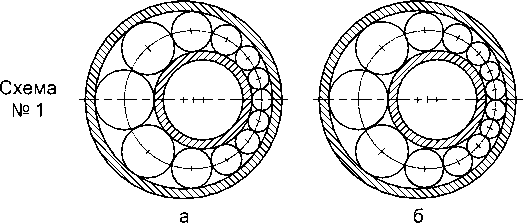
Схема № 2

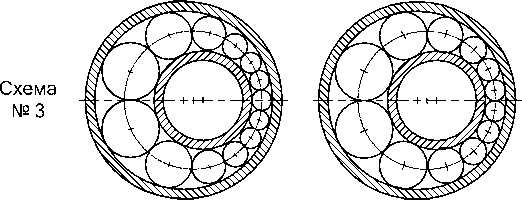
Схема № 4

в                                г

Рис. 1. Варианты структурных симметричных схем ЭМК

Используя полученные данные, выполнен синтез диаграмм, позволяющих реализовать анализ взаимозависимости геометрических параметров ЭМК для всех вариантов структурных схем по обоим направлениям ввода поправки, а также как при наличии, так и при отсутствии зазора между телами качения (см. рис. 2 и 3).

Анализ диаграмм (см. рис. 2) показывает, что функциональные зависимости для любого вида структурной схемы ЭМК имеют одинаковый параболический характер изменения величины угла подъема эксцентрика ЭМК от радиусов тел качения. Максимальные величины угла подъема эксцентрика принимают для промежуточных тел качения, имеющих радиусы, лежащие в середине диапазона величин данного параметра для любого вида структурной схемы эксцентрикового механизма качения, как при наличии, так и при отсутствии зазора между телами качения при обоих направлениях ввода поправки. Рост значения угла подъема эксцентрика наблюдается по мере приближения величин радиусов промежуточных тел качения к середине диапазона величин данного параметра. В то же время минимальные значения угла подъема эксцентрика характерны как для максимальных, так и для минимальных тел качения ЭМК для всех видов структурных схем эксцентрикового механизма по обоим направлениям ввода поправки, а также как при наличии, так и при отсутствии зазора между телами качения.

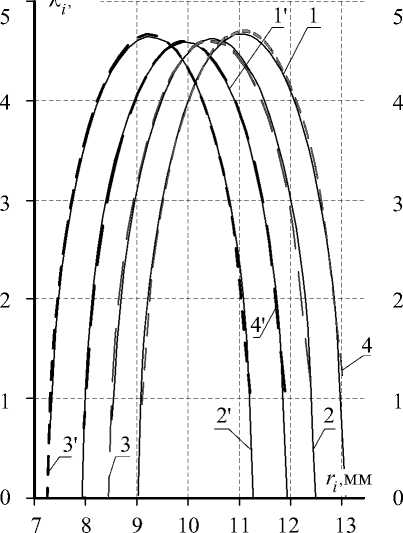
а (без зазора между телами качения)

б (с зазором между телами качения)

Рис. 2. Диаграммы изменения угла подъема эксцентрика ЭМК от радиусов тел качения:

1, 2, 3,4 - ввод поправки по R 1 ; Г, 2', 3', 4'- ввод поправки по R 2

Ввод поправки в расчет геометрических параметров эксцентрикового механизма качения по радиусу дорожки качения внутреннего кольца вызывает смещение функциональных кривых в направлении положительных значений оси радиусов тел качения ЭМК (см. рис. 2).

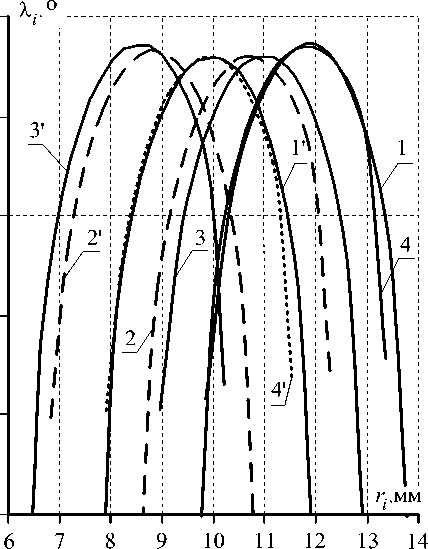
Анализ диаграмм (см. рис. 3) показывает, что функциональные зависимости для любой схемы эксцентрикового механизма качения имеют одинаковый косинусоидальный характер изменения величин радиусов тел качения. Рост значения угла положения сопровождается уменьшением радиусов тел качения для любого вида структурной схемы эксцентрикового механизма качения, как при наличии, так и при отсутствии зазора между телами качения при обоих направлениях ввода поправки в расчет геометрических параметров.

Зависимости для структурных схем эксцентрикового механизма качения № 1 (см. рис. 1, а ) и № 4 (см. рис. 1, г ), а также № 2 (см. рис. 1, б ) и № 3 (см. см. рис. 1, в ) представлены практически идентичными кривыми при исполнении без зазора (см. рис. 3, а ). При наличии зазора подобное явление характерно только для величин радиусов промежуточных тел качения для этих же видов структурных схем эксцентрикового механизма качения (см. рис. 3, б ). Радиусы тел качения в структурных схемах ЭМК № 2 (см. рис. 1, б ) и № 3 (см. рис. 1, в ) несколько меньше, чем в структурных схемах эксцентрикового механизма качения № 1 (см. рис. 1, а ) и № 4 (см. рис. 1, г ), при одинаковых исходных параметрах независимо от ввода поправки и наличия или отсутствия зазора (см. рис. 3).

При вводе поправки по радиусу дорожки качения наружного кольца для любого варианта структурной схемы ЭМК величина данного параметра уменьшается при неизменном радиусе дорожки качения внутреннего кольца, что вызывает рост количества тел качения и уменьшение их радиусов, как при наличии, так и при отсутствии зазора между телами качения (см. рис. 3). Ввод поправки по радиусу дорожки качения внутреннего кольца для любого вида структурной схемы эксцентрикового механизма качения приводит к снижению величины данного параметра, что способствует увеличению радиусов тел качения при минимальном их количестве как при наличии, так и при отсутствии зазора между данными звеньями.

Очевидно, что наличие зазора между телами качения позволяет уменьшить их количество при любом виде структурной схемы ЭМК для любого направления ввода поправки в расчет геометрических параметров.

Однако минимальное количество тел качения удалось получить только для структурной схемы эксцентрикового механизма качения № 4 (см. рис. 1, г ) при вводе поправки по радиусу дорожки качения внутреннего кольца при одинаковых исходных данных.

Максимально возможное число тел качения при этих же значениях исходных данных получено для нескольких структурных схем ЭМК № 1, 2 и 3 (рис. 1, а – в ) при вводе поправки в расчет геометрических параметров эксцентрикового механизма качения по радиусу дорожки качения наружного кольца.

r i , мм

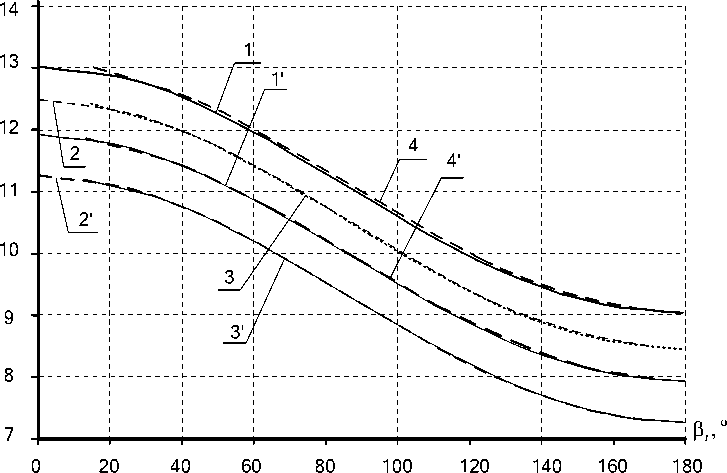
а (без зазора между телами качения)

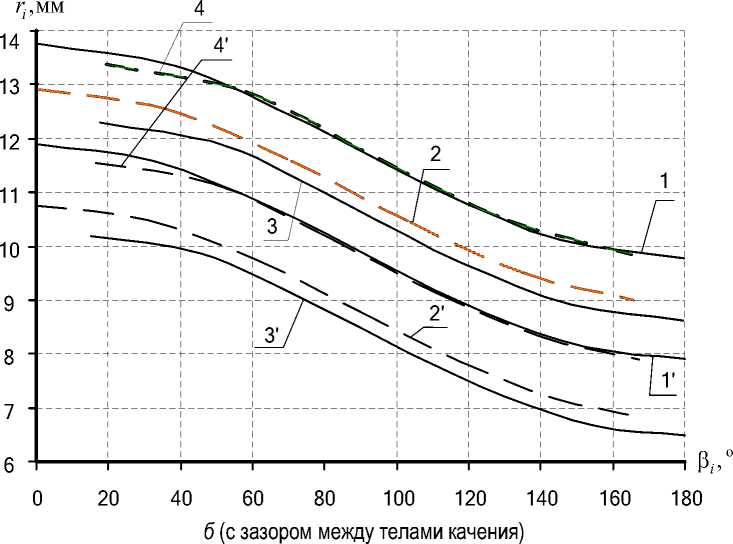
Рис. 3. Диаграмма изменения радиусов от угла положения тел качения:

1, 2, 3,4 - ввод поправки по R i ; 1', 2', 3', 4'- ввод поправки по R 2

Выводы. В результате проведенных исследований установлено, что угол подъема эксцентрика в зависимости от радиуса тел качения изменяется для любого вида структурной схемы ЭМК по параболическому закону, а радиус тел качения в зависимости от величины угла его положения изменяется по косинусоидальному закону, что характерно для любого вида структурной схемы эксцентрикового механизма качения. Выявлено, что направление ввода поправки в расчет геометрических параметров ЭМК, а также наличие или отсутствие зазора между телами качения не оказывает влияния на характер взаимодействия геометрических параметров ЭМК. Наличие четырех видов структурных схем позволяет получить шестнадцать возможных вариантов сочетаний величин геометрических параметров эксцентрикового механизма качения, что создает возможность для проведения сравнительного анализа полученных результатов и осуществления выбора окончательного решения таким образом, чтобы он наилучшим образом удовлетворял заданным критериям. Применение программного комплекса «Эксцентрик» на данном этапе обеспечит сокращение времени и трудоемкости данного процесса, а также, несомненно, создаст условия для повышения эффективности теоретических исследований ЭМК.