Анализ взвешенной процедуры Ширяева-Робертса в задаче обнаружения разладки для моделей снеизвестными параметрами после разладки

В работе [1] рассматривалась задача последовательного обнаружения разладки — изменения свойств случайного процесса, в которой его свойства были известны до и после разладки. Практический интерес вызывает задача, когда свойства случайного процесса после разладки до конца неизвестны. В такой задаче для обнаружения разладки логично применить взвешенные процедуры обнаружения разладки (это процедуры, в которых учитывается вероятностное пространство, элементарные события которого — случайный процесс после разладки с определенными свойствами, и задана вероятность наступления соответствующего элементарного события).

Напомним, задача последовательного обнаружения разладки — пока наблюдение за случайным процессом соответствует ожидаемому, следует продолжать наблюдение и обнаруживать изменение (разладку) как можно скорее после разладки. В работе [1] было показано, что в байесовской постановке (момент разладки — неизвестная и случайная величина) процедура Ширяева-Робертса показывает схожие характеристики с оптимальной процедурой Ширяева, но, в отличие от нее, не использует априорное распределение момента разладки. По этой причине процедура Ширяева-Робертса больше подходит для решения практических задач. В другой работе [2] было показано, что взвешенная процедура Ширяева-Робертса асимптотически оптимальна в классе процедур с заданным уровнем максимальной условной вероятностью ложной тревоги, а также в минимаксной постановке (момент разладки — неизвестная, но неслучайная величина). Поэтому интересно исследовать, насколько сильно в различных постановках проигрывает взвешенная процедура Ширяева-Робертса, настроенная на несколько возможных параметров случайного процесса после разладки, процедуре Ширяева-Робертса, настроенной на известные свойства случайного процесса после разладки.

В данной работе используются две модели наблюдаемого случайного процесса: гауссовский процесс и процесс авторегрессии 1 порядка. Для первой модели рассмотрим байесовский подход, а для второй модели рассмотрим минимаксный подход. На рис. 1 представлен процесс авторегрессии 1 порядка и взвешенная процедура обнаружения разладки, состоящая из взвешенной суммы трех процедур, настроенных на различные параметры случайного процесса после разладки.

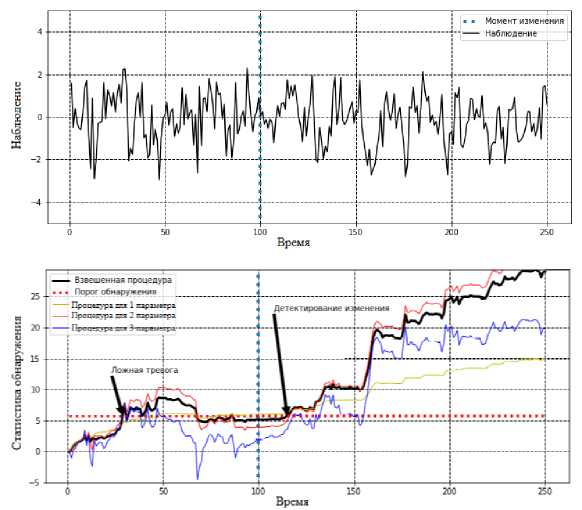
Рис. 1. Пример задачи обнаружения разладки взвешенной процедурой Ширяева-Робертса.

2.    Модель

Пусть {X_n} — наблюдаемьій процесс, где п = {0,1, 2,... }. До изменения он описывается распределением Р^, после изменения — Pq. В байесовской постановке изменение происходит в неизвестный и случайный момент времени v, v Е Z y = {0,1, 2,... }. Обозначим P j (Xⁿ), j = to, 0 — плотность распределения Р^, г де X ⁿ = (X 1 ,..., X_n) Тогда, если зафиксирован момент изменения v Е Z₊, плотность p_V (Xⁿ) = p(Xⁿ|v) является комбинацией плотностей до и после момента изменения:

p_v (Xⁿ) = p. X ) • Po(X:₊i|X") =

V                    n

= Г^*|X^i-i) • П Ро(Х_г|Х^г-і) i = 1                 i=v+1

где ХП = (Xi,..., X_n) и p j (X_n|X^n-i) — условная плотность X_n при условии X^n-i. Пусть v — порядковый номер последнего наблюдения перед изменением.

Как было упомянуто выше, в данной задаче (для гауссовской модели) рассматривается байесовская постановка: постановка задачи, когда момент изменения — случайная величина, независимая от наблюдений, с априорным распределением вероятности л к = Р (v = к), к = 0,1, 2,.... Как и в [1] будем считать, что момент изменения v получается из геометрического распределения

Р (v = к) = р(1 — р)^к для к = 0,1, 2,...,

где 0 < р <  1.

Процедура обнаружения разладки представляет собой время остановки Т для наблюдаемого процесса {X_n}. Когда Т 6 v, это означает, что произошла ложная тревога. Хорошая процедура обнаружения гарантирует при низком уровне ложной тревоги маленькую задержку в обнаружении Т — v.

В байесовской постановке риск, связанный с задержкой обнаружения, измеряется средней задержкой обнаружения [3]:

ADD(T ) = Е ^л[Т — v|Т > v] =

∞

^^kEk[Т — к|Т > к]Р^(Т > к)

к=0 _______________________________

1 — РҒА(Т )

а риск ложной тревоги измеряется как взвешенная вероятность ложной тревоги [3]:

∞

РҒА(Т ) = Р"(Т 6 v ) = ^л_кР^(Т 6 к),                   (4)

к=1

где Рк и Е_к — вероятность и соответствующее ей ожидание момента изменения v = к Е Zy.

Для модели авторегрессии 1 порядка рассматривается минимаксный подход: подход, когда момент изменения — неизвестная и неслучайная величина [3]. В минимаксной постановке, риск, связанный с риском ложного срабатывания, оценивается максимальной локальной условной вероятностью ложной тревоги:

РСРҒА(Т ) =   sup Р^(Т >  к + ш*|Т > к).

1 6 к 6 к *- т *

В минимаксной постановке считается максимальная средняя задержка обнаружения ADD в определенном окне.

• 3.    Процедуры обнаружения

Если « Н_к : v = к» и «Н^ : v = то» — гипотезы, что разладка наступает в момент времени 0 6 к < той что разладка не наступает никогда, тогда получаем отношение правдоподобия между гипотезами, используя (1):

,   = р_к ( Х ^п) = р( Х ^к ) • Po( X £₊₁| X ^fc)

'^к,п   р^( х ^п)           р Х

П ?=1      х | х ^г-1) • п Г=мі ро(Хг| х ^г-1)

П ?=1 р . ( Уг Х ^г ,

Л о у х к < п.

гД+і р^(Х г \ Х ^г-1) ’

Пусть £_г = ро(Х_г|Х^{г 1})/р^,(Х_г\ Х ^{г 1}). Тогда из [4] статистика Ширяева-Робертса будет считаться:

п п

/-■    52 П^ = (1 + Я„-1) £п,  п > 1, Ro =0.(6)

к=1г=к

Время остановки процедуры Ширяева-Робертса:

ТА = inf{п > 1 : Rn > А},  А > 0,(7)

где А — порог.

Для взвешенной процедуры Ширяева-Робертса необходима статистика, настроенная на каждый из возможных после разладки параметров наблюдения Ө 3 [5]:

Rn(e3) = (1 + Rn-1(e3)) £п(Ө3), п > 1, Ro = 0.(8)

С учетом веса (вероятности) принять каждый из параметров наблюдения Ө 3 после разладки, получается взвешенная статистика Ширяева-Робертса:

N

Rn = £w (Өз )Дп(Өз), з=г где W(Ө) — функция распрсделепия Ө.

Тогда время остановки для взвешенной процедуры Ширяева-Робертса записывается как:

Т_в = inf{п > 1 : ДП > В}, В> 0,                         (9)

где В — порог.

В данной работе неизвестным параметром после разладки будем считать среднее Ө. Также будем считать, что каждое из возможных значений среднего Ө 3 равновероятно, для каждого значения Ө 3 значение функции распределения будет W(Ө 3 ) = N, ^гД^е Х д — число значении Ө3.

• 4.    Гауссовская модель

Процесс наблюдения {Х_п} гауссовской модели удовлетворяет гауссову распределению N"(0,02) до разладки и N" (Ө,іт²) после:

Х п = Ө1^_{п>,_} + ^п, п > 1,                              (10)

Отношение правдоподобия, используемое в (6) и (8), в этом случае:

£ п = exp

{0^{2 Хп}

б2

2о2

Отношение сигнал-шум определяется как I = Ө2/2а², а² = 1.

Для оценки характеристик процедур обнаружения в данной задаче, будем использовать метод Монте-Карло. Для каждого прогона Монте-Карло мы симулируем двойную стохастическую модель: (X_n,v ) — наблюдение согласно (10) и момент изменения согласно (2). В каждом г-м, г = 1,..., N , прогоне Монте-Карло находится время остановки Ті для обычной (7) и взвешенной (9) процедур Ширяева-Робертса. Считается, что в конкретном г-м прогоне Монте-Карло г = 1,..., N происходит ложная тревога, если Т і < vp

Оценка вероятности ложной тревоги (4):

____       1 "

^PFA(^T ) = _N £%<„,}■ і =1

Оценка Монте-Карло средней задержки обнаружения (3):

1 \г                        1

ADD(T) = - £(T - Vi)1_Ti > _{Vi }}---.

^N              1 - PFA(T )

Число прогонов Монте-Карло N = д^, г де А — это точность, а а — ограничение для частоты возникновения ложных тревог.

4.1.    Результаты компьютерного моделирования

Напомним, для исследования была выбрана процедура Ширяева-Робертса, поскольку, как показано в [1], она показывает почти такие же характеристики, как и оптимальная в байесовской постановке процедура Ширяева, но при этом не использует априорное распределение момента разладки. По этой причине процедура Ширяева-Робертса является более удачной с точки зрения практической применимости. Метод Монте-Карло позволяет получить характеристики процедур обнаружения с высокой точностью.

Параметры симуляций.

• 1)    Отношение сигнал-шум после разладки I = 0.5; 0.245; 0.125, т.е. среднее после разладки Ө = 1.0; 0.7; 0.5;.

• 2)    Параметры геометрического распределения: р = 0.2; 0.1; 0.05.

• 3)    Верхняя граница PFA: а = 0.1; 0.05; 0.01.

• 4)    Сетка параметров для процедуры взвешенного среднего:

Өб = {-1.0; -0.6; -0.2; 0.2; 0.6; 1.0}, Ө20 = {-1.0; -0.9; -0.8;... 0.8;0.9;1.0} - с пропуском 0.

В табл. 1-3 приведены сравнительные характеристики процедуры Ширяева-Робертса, настроенной на известные после разладки параметры и взвешенной процедуры Ширяева-Робертса, настроенной на б и на 20 возможных параметров наблюдения после разладки. Из этих исследований мы делаем следующие выводы:

• 1)    Как и ожидалось, процедура Ширяева-Робертса, настроенная на известные после разладки параметры, работает лучше, чем взвешенные процедуры Ширяева-Робертса, настроенные на несколько возможных после разладки параметров. Однако этот проигрыш в задержке обнаружения не является очень большим (не более 20%).

• 2)    Как и ожидалось, проигрыш в задержке обнаружения взвешенными процедурами обнаружения, настроенных на несколько возможных параметров после разладки, относительно процедуры Ширяева-Робертса, настроенной на известные параметры после разладки, увеличивается с уменьшением отношения сигнал-шум I.

• 3)    Взвешенная процедура Ширяева-Робертса, настроенная на б возможных параметров после разладки, когда один из этих шести является реальным, демонстрирует характеристики обнаружения немного лучше, чем взвешенная процедура Ширяева-Робертса, настроенная на 20 возможных параметров, но начинает ей проигрывать, когда реальный параметр близок, но в точности не равен ни одному из шести возможных параметров после разладки в

отличие от взвешенной процедуры Ширяева-Робертса, которая настроена на 20 возможных параметров после разладки, среди которых еств реальный.

Таблица!

Характеристики процедур обнаружения для гауссовской модели наблюдения, р = 0.2

р = 0.2
I	a	PFA	РҒА 6У	PFA ^	ADD	ADD ^	add v
0.500	0.1	0.09464	0.09471	0.09431	3.57	4.39	4.42
0.500	0.05	0.04762	0.04732	0.04718	4.46	5.31	5.33
0.500	0.01	0.00980	0.00983	0.00975	6.70	7.48	7.49
0.245	0.1	0.09373	0.09240	0.09154	4.80	6.00	5.96
0.245	0.05	0.04638	0.04697	0.04720	6.22	7.58	7.47
0.245	0.01	0.00967	0.00993	0.00951	9.70	11.46	11.28
0.125	0.1	0.09486	0.09454	0.09471	5.84	7.49	7.38
0.125	0.05	0.04908	0.04773	0.04708	7.66	10.22	9.90
0.125	0.01	0.00932	0.00989	0.00942	12.92	17.02	16.44

Т а б л и ц а 2

Характеристики процедур обнаружения для гауссовской модели наблюдения, р = 0.1

р = 0.1
I	a	PFA	PFA ^	PFA V	ADD	ADD ^	add2V
0.500	0.1	0.09094	0.09171	0.09104	4.90	5.96	6.02
0.500	0.05	0.04838	0.04708	0.04682	5.91	7.06	7.09
0.500	0.01	0.00972	0.00958	0.00970	8.55	9.66	9.67
0.245	0.1	0.09717	0.09850	0.09866	6.96	8.65	8.62
0.245	0.05	0.04703	0.04900	0.04847	8.95	10.75	10.68
0.245	0.01	0.00936	0.00953	0.00946	13.54	15.83	15.53
0.125	0.1	0.09504	0.09793	0.09763	9.35	12.21	12.00
0.125	0.05	0.04841	0.04812	0.04883	12.18	15.94	15.61
0.125	0.01	0.00923	0.00954	0.00944	19.64	25.44	24.50

Т а б л и ц а 3

Характеристики процедур обнаружения для гауссовской модели наблюдения, р = 0.05

р = 0.05
I	a	PFA	PFA ^	PFA V	ADD	ADD6V	ADD^
0.500	0.1	0.09203	0.09202	0.09167	6.26	7.52	7.60
0.500	0.05	0.04694	0.04562	0.04521	7.47	8.82	8.90
0.500	0.01	0.00985	0.00953	0.00950	10.29	11.66	11.75
0.245	0.1	0.09336	0.09200	0.09313	9.65	11.86	11.73
0.245	0.05	0.04607	0.04501	0.04573	11.96	14.32	14.19
0.245	0.01	0.00910	0.00932	0.00942	17.34	19.85	19.56
0.125	0.1	0.09138	0.09223	0.09189	13.98	18.16	17.83
0.125	0.05	0.04610	0.04523	0.04574	17.69	22.78	22.22
0.125	0.01	0.00935	0.00929	0.00949	26.66	33.61	32.50

5.    Модель авторегрессии 1 порядка

Процесс наблюдения {Хп} модели авторегресси 1 порядка удовлетворяет следующему выражению:

(И)

Хп = Ө!^}Хп-1 + U П > 1, Хо = 0, где Сп ~ гауссовский шум с единичной дисперсией.

Из [5] отношение правдоподобия, используемое в (6) и (8), в этом случае:

L n = exp ^ХпХп-1 -

^{Ө Х}п-1

} •

Отношение сигнал-шум в этом случае: I = 2(1 — 2 6* 2)'

Для оценки характеристик процедур обнаружения в данной задаче будем использовать метод Монте-Карло. Так как мы рассматриваем минимаксный подход, момент изменения v — фиксированное число. Для каждого прогона Монте-Карло мы симулируем наблюдение Х п согласно (11), а также находим время остановки T для обычной (7) и взвешенной (9) процедур Ширяева-Робертса. Оценка локальной условной вероятности ложной тревоги (5):

LCPFA(T ) =   sup   P^(T > k) =

1

sup

16k6k* -m*

P^ (k 6T + m*) P^(T > k)

sup

16k6k* -m*

Nk,k+m* N

·

N

"XT =   suP

^Nk   16k6k*-m*

Nk,k+m*

Nk   ’

где Nk,k+_m* — количество прогонов Монте-Карло, в которых время остановки T попадает в интервал [к; к+m*), a Nk — количество прогонов Монте-Карло, в которых время остановки 7 > к.

• 5.1.    Результаты компьютерного моделирования

Выбор порога для процедур обнаружения.

Для того, чтобы обеспечить LCPF A(T) 6 Р, выбираем порог, как в [5]

где

^А =

1 — а

Са

а =

Р (1 — С )^k*.

1 + Р ;

С (1 + |logP\)H.

где. в свою очередь. k* = Н • m*. a m* = | log Д|(1 + | logР|).

Параметры симуляций.

• 1)    Н = 1.2.

• 2)    Отношение сигнал-шум после разладки I = 2.132; 0.889; 0.48; 0.281; 0.167; 0.095, т.е. среднее после разладки Ө = 0.9; 0.8; 0.7; 0.6; 0.5; 0.4.

• 3)    Момент изменения v = 0; 10.

• 4)    Верхняя Гранина PFA; Р = 0.01.

• 5)    Сетка параметров для процедуры взвешенного среднего:

Ө18 = {—0.9; —0.8; —0.7;... 0.7; 0.8; 0.9} — с пропуском 0.

Результаты симуляций Монте-Карло представлены в табл. 4. Из этих исследований мы делаем следующие выводы:

• 1)    Для относительно больших значений сигнал-шум после изменения правило Ширяева-Робертса лишь незначительно превосходит взвешенную процедуру Ширяева-Робертса, но с уменьшением эта разница увеличивается.

• 2)    Как и ожидалось, наихудший момент изменения ? = 0.

6.    Заключение

Т а б л и ц а 4

Характеристики процедур обнаружения для модели наблюдения авторегрессии 1 порядка

? = 0; 3 = 0.01
I	LCPFA	LCPFA^	ADD	ADD^
2.132	0.0080	0.0079	11.08	11.74
0.889	0.0073	0.0073	13.72	14.72
0.480	0.0070	0.0071	17.52	18.97
0.281	0.0065	0.0065	23.15	25.32
0.167	0.0049	0.0049	31.84	36.35
0.095	0.0024	0.0025	45.88	59.57
? = 10; 3 = 0.01
I	LCPFA	LCPFA^	ADD	ADD^
2.132	0.0080	0.0079	9.62	10.05
0.889	0.0073	0.0073	11.98	12.72
0.480	0.0070	0.0071	15.30	16.59
0.281	0.0065	0.0065	20.34	22.55
0.167	0.0049	0.0049	28.01	32.96
0.095	0.0024	0.0025	40.83	55.34

Было проведено исследование характеристик обнаружения взвешенной процедуры Ширяева-Робертса для задачи с неизвестным параметром наблюдения после разладки. Характеристики взвешенной процедуры Ширяева-Робертса сравнивались с характеристиками процедуры Ширяева-Робертса, настроенной на известные после разладки параметры. Критерием качества для сравнения служила средняя задержка обнаружения при ограниченной вероятности ложной тревоги (модель гауссовского наблюдения) и при ограниченной локальной условной вероятности ложной тревоги (модель наблюдения авторегрессии 1 порядка). Результаты представлены в табл. 1-4. Показано, что взвешенная процедура Ширяева-Робертса проигрывает процедуре Ширяева-Робертса, настроенной на известные после разладки параметры, но незначительно. В свою очередь, взвешенная процедура, которая настроена на меньшее количество параметров, среди которых в точности нет реального параметра после разладки, проигрывает взвешенной процедуре, с большим количеством параметров, среди которых присутствует в точности параметр после разладки. Следовательно, идея применения взвешенных процедур, в случае, когда параметры наблюдения после разладки до конца неизвестны, является удачной. Результаты исследования очень полезны для большинства задач, так как на практике почти всегда параметры после разладки до конца неизвестны.

Работа была поддержана грантом Россиского Научного Фонда 18-19-00452 в МФТИ.