Анализ зависимости вторично-эмиссионного тока и рентгеновского излучения от положения луча относительно стыка при электронно-лучевой сварке

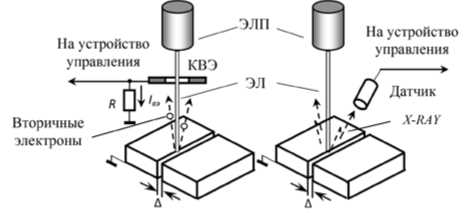
На рис. 2 приведены примеры расположения датчика вторичных электронов (рис. 2а) и датчика рентгеновского излучения (рис. 2б) [1]. Ток вторичных электронов I вэ может быть представлен следующим образом [2]:

I вэ = k вд ⋅ϕ⋅ I л                 (1)

где I л – ток луча; k вд – коэффициент, учитывающий количество вторичных электронов, попадающих на датчик; φ – коэффициент вторичной эмиссии свариваемых материалов; I л – ток электронного луча.

а)                б)

Рис. 1. Схемы приема сигналов: ЭЛП – электронно-лучевая пушка; ЭЛ – электронный луч; КВЭ – коллектор (датчик) вторичных электронов

а)                               б)

Рис. 2. Расположение датчиков

j(Х,У ) =

—

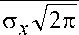
exp

⁽ x ^s x ) 2^

x

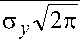
exp

(y-sy

2a

y

где σ х , σ у – среднеквадратические отклонения электронов от оси пучка по соответствующим осям; ε х , ε у – математические ожидания – положение оси луча в координатах х , у (рис. 3).

Интенсивность J рентгеновского излучения определяется выражением [3]:

J = C - k рд - U - Z - 1 л (2)

где C – коэффициент пропорциональности ( С ≈10^-9, V ^-1 [3]); k рд – коэффициент, учитывающий долю излучения, приходящего на поверхность датчика; U – ускоряющее напряжение; Z – атомный номер свариваемого материала.

Выражения (1) и (2) показывают, что I вэ и J с точностью до коэффициентов определяются током луча I л . Можно предположить, что и зависимости I кв и J от положения луча относительно стыка имеют одинаковый характер. А это позволяет использовать один и тот же математический аппарат для исследования этих зависимостей.

Формализация задачи. Плотность тока в пучке электронов неодинакова по его сечению и носит вероятностный характер, поэтому ток луча I л представляют через функцию распределения электронов по соответствующим осям [4], и выражения (1) и (2) можно записать в следующем виде:

im

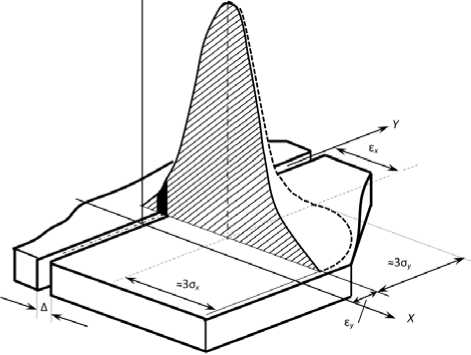
Рис. 3. К расчету I вэ и J

В пределах пятна нагрева поверхность свариваемых деталей можно считать однородной в направлении оси ОY (вдоль стыка). Тогда I вэ и J не зависят от у . Учитывая, что

м

J

-м

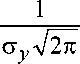
exp

^-

( y -^£ y)²

2 а У

dy = 1

м м

I кв = ^k вэ I л J / ф ( x,y ) j ( x,y ) dxdy

-м -м

;

как интеграл от плотности распределения в

бес-

конечных пределах [5], запишем выражения для

I вэ и J :

I вэ

м м

J = Ck рд U ² 1 л J J Z ( x,y ) j ( x,y ) dxdy

-м -м

= k вэ I л a V2n

м

J ф(x) exp

-м

(x -s)2 2a2

dx

J =

гдe j ( x,y ) – плотность распределения тока пучка электронов в координатах х , у , причем

Сk рд U ² I л

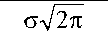
м

J Z(x) exp

-м

—

(x - s)2 2a2

dx

м

J

м

J j ( x, У ) dxdy = 1

-м -м

Плотность j ( х , у ) представляют нормальным законом распределения [4]:

Последние соотношения свидетельствуют об одинаковой (экстремальной) зависимости вторично-эмиссионного тока и рентгеновского излучения от положения ε электронного луча относительно стыка, и зависимости I вэ и J при одной и той же плотности распределения электронов в

луче определяются соответствующими постоянными коэффициентами и природой рассматри-

ваемого явления, определяемого переменными коэффициентами ф( х ) и Z ( х ).

Частные случаи.

1. Если осуществляется сварка однородных материалов, то ф и Z не зависят от х , и с учетом того, что вторичная эмиссия и рентгеновское из-

лучение из зазора в стыке отсутствуют, рассмат-

риваемые соотношения (5), (6) примут вид:

I вэ

= k вэ I л Ф1 1 ^-

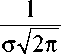
А / 2

f exp

-А / 2

(x - s)2 ч;^

dx j.

;

при сварке однородных материалов соответствует совпадению координат луча и стыка. При этом уменьшение зазора в стыке (рис. 4,а) или увеличение среднеквадратического отклонения электронов от оси луча (рис. 4,б) приводит к уменьшению относительного изменения этих зависимостей. Последнее может служить критерием для оценки точности определения координат луча.

2. При ЭЛС разнородных материалов необходимо учитывать зависимости ф( х ) и Z ( х ). Например, при сварке меди ( Z Cu =29) и стали ( Zfc =26) выражение (6) для J в относительных

единицах примет вид:

J = Ck_pgU ² 1 _л Z h

; V2n

А / 2

f ^exp

-А / 2

^{( x -} e ) ²

2 ; 2

dx >

где A - зазор в стыке (рис. 3).

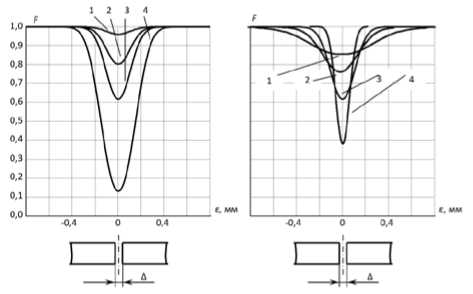
На рис. 4 представлены графики зависимости функции F от положения е луча относительно стыка при ЭЛС однородных материалов:

F = И -

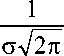
А / 2

f ^exp

-А / 2

(x - s)2

2-

dx •

J отн. = Z cu

-А / 2 f exp

-ГО

(x - s)2

2;

dx +

-А / 2

+ Z Fe f exp

-ГО

(x - s)2

2;

dx

, (9)

где

_T _ J ; V2n J отн. =         5

Сk рд U ² I л

На рис. 5а приведены результаты расчета по формуле (9). На рис. 5б показана зависимость J отн/ Z cu .

а)                             б)

Рис. 4. Расчетные зависимости F от положения луча относительно стыка:

а) - а = const = 0,1 мм, A = var ; 1 - A = 0,01 мм; 2 - A = 0,05 мм; 3 - A = 0,1 мм; 4 - A = 0,3 мм; б) - A = const = 0,1 мм, а = var ; 1 - а = 0,25 мм; 2 - а = 0,15 мм; 3 - а = 0,1 мм; 4 - а = 0,05 мм.

Для получения абсолютных значений достаточно ординаты графиков умножить на соответствующие коэффициенты:

I вэ = k вэ ^- 1хф •F ;

JС рд и • I л Z-F .

Из соотношений (7), (8) и графиков видно, что минимум рассматриваемых зависимостей

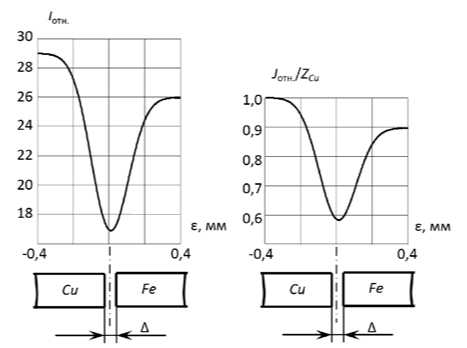
Рис. 5. Зависимость интенсивности РИ от положения луча относительно стыка при ЭЛС разнородных материалов.

Из графиков видно, что при ЭЛС разнородных металлов ветви характеристик имеют разные наклоны. Металлу с большим атомным номером соответствует больший наклон (интенсивность РИ пропорциональна атомному номеру). По этой же причине значения насыщения интенсивности при полном выходе луча на одну из деталей отличаются на величину, зависящую от атомного номера материала. В относительных единицах эти значения для cu и Fe равны их атомным номерам - 29 и 26, соответственно (рис. 5а).

Другой особенностью этих характеристик является смещение экстремума в сторону материала с меньшим атомным номером. Это связано с тем, что координата экстремума определяется равенством излучения с соответствующих поверхностей, которое пропорционально току пучка электронов, а, следовательно, и площади части пятна, находящейся на данном металле. Так, как Z Cu > Z Fe , то для выполнения названного равенства необходимо, чтобы площадь пятна на стальной детали была больше площади пятна на медной детали. В связи с этим луч оказывается смещенным в сторону стальной детали. Следовательно, положение стыка не совпадает с положением экстремума характеристики, что необходимо учитывать при ЭЛС разнородных материалов.

Характер смещения экстремума при различном зазоре ∆ представлен на рис. 6. Графики построены в соответствии с уравнением (9).

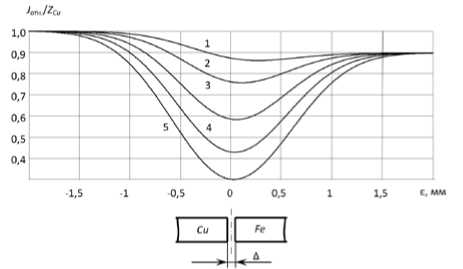
Рис. 6. Зависимости интенсивности РИ от положения луча относительно стыка при ЭЛС разнородных металлов:

σ = 0,1 мм; 1 – ∆ = 0,02 мм; 2 – ∆ = 0,05 мм; 3 – ∆ = 0,1 мм; 4 – ∆ = 0,15 мм; 5 – ∆ = 0,2 мм

Видно, что заметные рассогласования положений экстремума характеристик и стыка проявляются при отношении ∆/σ ≤ 1. Такой случай является наиболее распространенным на практике и еще раз подтверждает необходимость учета этого рассогласования. Дифференцируя уравнение (9) по ε, и приравнивая производную нулю, можно найти ε 0 – абсциссу экстремума ε 0 и зависимость ее от зазора в стыке ∆:

d J отн. = 0 d ε

Решением оказывается следующее соотношение: _{ε 0 ≈} α ( σ ) _{= 0}

∆       ,        (10)

где α – параметр, зависящий от σ (табл. 1).

Таблица 1. Изменение α в зависимости от σ

σ	0,1	0,2	0,3	0,4	0,5
α	0,0011	0,0044	0,0098	0,017	0,027

На рис. 7 представлены графики зависимости положения ε 0 экстремума зависимости J ( ε ) от зазора в стыке для различных σ . Из графиков видно, что при малых зазорах в стыке (что является характерным для ЭЛС) ε 0 может иметь значения, превышающие допустимую погрешность совмещения луча со стыком свариваемых деталей. При реализации устройств автоматического слежения за стыком с использованием экстремальной зависимости J от положения луча относительно стыка необходимо учитывать поправку в соответствии с выражением (10).

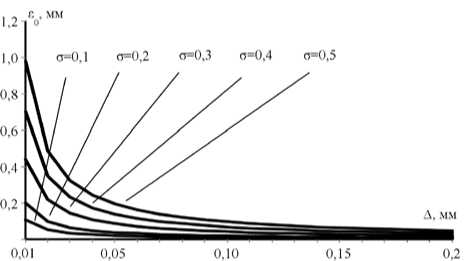
Рис. 7. Зависимость положения ε 0 экстремума от зазора ∆ в стыке при ЭЛС разнородных материалов

Аналогичные результаты получены при анализе зависимостей вторично-эмиссионного тока от положения луча относительно стыка. При ЭЛС разнородных материалов смещение экстремума зависимости I кв от ε происходит в сторону материала с меньшим коэффициентом вторичной эмиссии (в рассматриваемом случае – в сторону медной детали).

Функциональная схема устройства слежения за стыком. Устройство реализовано по классической схеме управления с отрицательной обратной связью (рис. 8) [6]. Если координаты луча х л и стыка х ст не совпадают, устройство управления формирует сигнал, который с помощью отклоняющей системы электронно-лучевой пушки преобразуется в перемещение луча до устранения рассогласования.

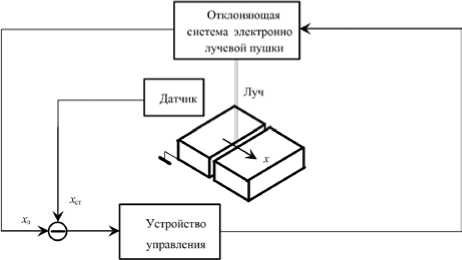
Рис. 8. Функциональная схема устройства автоматического слежения за стыком при ЭЛС эмиссионного тока смещается в сторону материала с меньшим коэффициентом вторичной эмиссии, а минимум рентгеновского излучения в сторону материала с меньшим атомным номером.

• 3.    Для анализа рассматриваемых зависимостей может быть применен одинаковый математический аппарат, а реализация устройств управления может быть осуществлена унифицированными аппаратными и программными средствами.