Анализ значимости и чувствительности результатов вероятностного анализа безопасности АЭС

Целью анализа значимости является идентификация важных событий с точки зрения вероятностных показателей безопасности [1].

Целью анализа чувствительности является [1]:

• 1)    Определение возможных зависимостей среди составляющих отказов, критериев успеха. и ошибок оператора, и влияния этих зависимостей на. вероятностный показатель безопасности.

• 2)    Моделирование предположений, которые могут потенциально влиять на результаты.

События, рассматриваемые в анализе значимости [2]:

• —    аварийная последовательность;

• —    исходные события;

• —    системные отказы;

• —    компоненты отказов;

• —    отказы по общей причине;

• —    ошибки оператора.

Показатели, рассматриваемые в анализе значимости [2]:

• —    частота, повреждения активной зоны;

• —    частота, аварийной последовательности;

• —    неготовность системы.

Анализ чувствительности состоит из двух частей: анализ чувствительности исходных данных и анализ чувствительности модели. Анализ чувствительности исходных данных состоит в исследовании влияния результатов изменений в исходных данных (например, частотах инициаторов, составляющих интенсивностях отказов, вероятности ошибки оператора. и т.д.) на. результаты В АБ. Чувствительность модели — степень влияния изменений модели на. результаты В АБ [2].

Анализ чувствительности выполняется для:

• —    событий по тестированию и восстановлению;

• —    ошибок оператора;

• —    отказов по общей причине;

• —    восстановления ошибок оператора;

• —    восстановления отказов оборудования.

Таким образом, результаты анализа, значимости помогают выбрать те базовые события, которые больше всего влияют на. вероятностные показатели безопасности. А анализ чувствительности помогает выбрать те базовые события, при которых относительно малые их изменения приводят к относительно большим изменениям вероятностных показателей безопасности.

• 1.    Методика анализа значимости

Анализ значимости — это анализ результатов квантификации с точки зрения вкладов различных групп базовых событий, исходных событий, аварийных последовательностей и других объектов анализа в суммарную частоту повреждения активной зоны [3].

Существуют два класса анализа значимости:

• 1)    качественный анализ значимости;

• 2)    количественный анализ значимости.

Качественный анализ значимости — вероятностный показатель безопасности, который получается из логической структуры моделей В АБ. Качественная оценка В АБ обеспечивает критерии, необходимые для анализа значимости составляющих вкладов в риск.

Количественный анализ значимости — анализ составляющих вероятностного показателя безопасности, полученных в результате количественной оценки В АБ.

В качестве показателей значимости используются следующие:

• —    показатель значимости Fussell-Vesely;

• —    инспекционный показатель значимости;

• —    линейный показатель значимости;

• —    нормированный показатель значимости;

• —    показатель увеличения риска;

• —    показатель снижения риска.

Показатели значимости для базовых событий

• 1)    Показатель значимости Fussell-Vesely. Показатель значимости Fussell-Vesely ( FV) события Е определен как относительный вклад события в вероятностный показатель безопасности и может быть представлен следующим образом:

  FV (Е ) =

  
  

Е Р {Е ПС,} г

CDF ’ где Cг — набор событий, {Е П Cг} — набор минимальных сечений, который включает событие Е. Р — вероятность.

• 2)    Инспекционный показатель значимости. Выражение вероятностного показателя безопасности в линейной зависимости от вероятности события Е с соответствующими параметрами а и Ь:

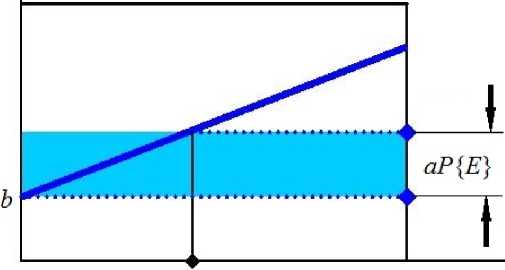
PSI = аР {Е} + Ь.

PSI

Р^

Probability

Рис. 1. Графическое представление контрольного показателя значимости

Контрольный показатель значимости (II) события Е может быть определен следующим образом (рис. 1):

II (Е) = аР {Е}.

• 3)    Линейный показатель значимости. Линейный показатель значимости события Е определен как линейный вклад в вероятностный показатель безопасности.

Линейный показатель значимости события Е может быть определен следующим образом:

ЬН(Е ) =       .

• 4)    Нормированный показатель значимости. Нормированный показатель значимости события Е определен как относительная зависимость вероятностного показателя безопасности от события. Нормированный показатель значимости может быть представлен как

Е Р {Е п с_г}

^NR(B ) = Е Р {Е П С} + Е Р {С, } ’ ^г                             3

где Сг — набор событий, {ЕПСД — набор минимальных сечений, включающий событие Е, С, — набор минимальных сечений, не включающий событие Е, Р — вероятность.

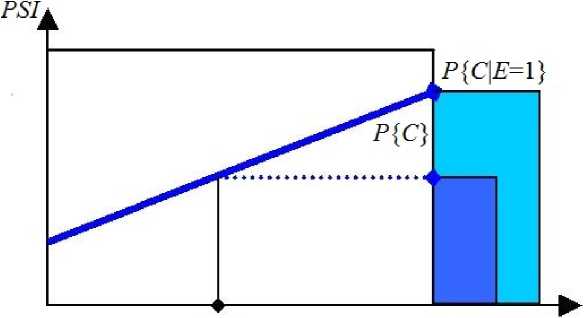
• 5)    Показатель возрастания риска. Показатель возрастания риска события Е определен как вероятность выполнения верхнего события С при отказе события Е. Показатель возрастания риска может быть представлен как (рис. 2):

  RAW (Е) =

  
  

  Р {С |Е = 1} Р {С }

  
  

где С — верхнее событие, Е = 1 — отказ события Е, Р{|} — условная вероятность.

Probability

Р№

Рис. 2. Графическое представление показателя возрастания риска.

• 6)    Показатель снижения риска. Показатель снижения риска события Е определен как вероятность выполнения верхнего события С при условии, что отказа, события нет. Показатель снижения риска, может быть получен следующим образом (рис. 3):

  RRW (Е ) =

  
  

  Р {С }

  Р {С |Е = 0} ’

  
  

где С — верхнее событие, Е = 0 — отказа со бытия нет, Р { } условная вероятность.

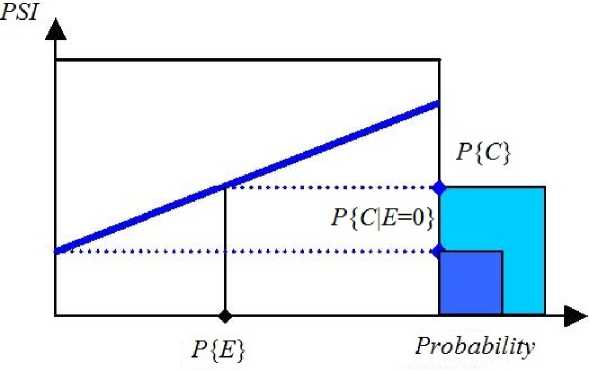
Рис. 3. Графическое представление показателя снижения риска.

Показатели значимости для систем

• 1)    Показатель значимости Fussell-Vesely системы S определен в условиях его влияния на. риск при условии, что все компоненты системы являются или работоспособными или отказовыми. Пусть E q — верхнее событие и Р { E q S = 0} представляет верхнее событие вероятностного показателя безопасности со всеми компонентами в системе S, являющейся работоспособной, и Р { E q S = 1} представляет верхнее событие ВПБ со всеми компонентами системы S в состоянии отказа. Показатель значимости Fussell-Vesely системы определен

  как

  
  

  FV (S) = 1 -

  
  

  Р { E q | s = 0} CDF

  
  

• 2)    Нормированный показатель значимости. Нормированный показатель значимости си

  стемы S определен как

  
  

  NR(S) = 1 -

  
  

£ Р{S = 0 П С} г

ЕРС} г где Сг — набор минимальных сечений, {S = 0 П СW набор минимальных сечений, который включает компоненты системы S, находящиеся в отказовом состоянии.

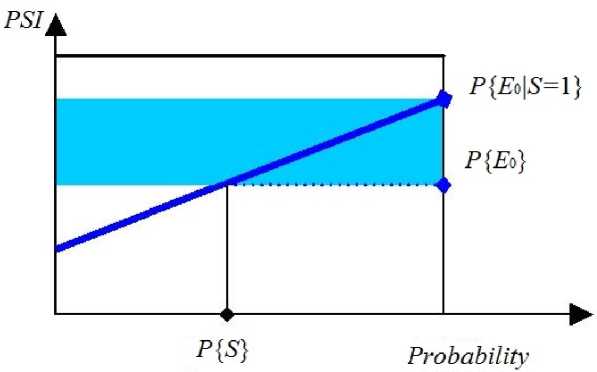
Рис. 4. Графическое представление показателя возрастания риска, для системы

• 3)    Показатель возрастания риска. Показатель возрастания риска системы S может быть определен как (рис. 4):

RAW(S) = Р { E q | S = 1} - Р { E q } .

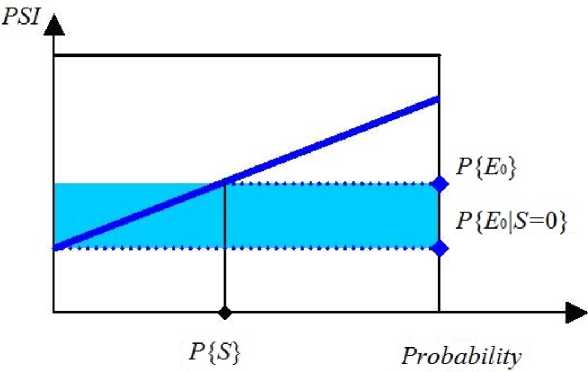
Рис. 5. Графическое представление показателя снижения риска, для системы

• 4)    Показатель снижения риска. Показатель снижения риска системы S может быть определен как (рис. 5):

• 2. Методика анализа чувствительности

RAW (S) = Р{Ео} — Р {Eo|S = 0}.                        (1)

Анализ чувствительности исследует влияние на. конечные результаты ВАБ допущений, сделанных в моделях, и данных по поводу потенциально важных, но точно неизвестных факторов [3].

При анализе чувствительности изменение данных или модели может приводить как к снижению вероятности реализации сечений, так и к ее повышению.

Существует два. основных типа, чувствительности:

— чувствительность к данным и

— чувствительность к модели.

Количественные показатели чувствительности

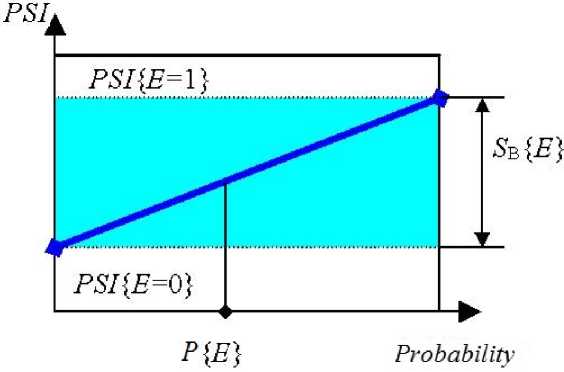
Рис. 6. Графическое представление чувствительности по Birnbaum

• 1)    Показатель чувствительности по Birnbaum события Е определен как скорость изменения вероятностного показателя безопасности относительно вероятности события Е

  (рис. 6):

  
  

  S_B (Е) =

  
  

  dPSI (Е ) dP{Е } "

  
  

• 2)    Показатель чувствительности зависимых отказов или ошибки оператора определен как изменение меры чувствительности из-за изменения вероятности зависимого отказа:

Sd = PSI(P{Е\Ed}, P{Ed}) - PSI(P{Е}, P{Ed}), где P{E|Ed} — вероятность отказа Е, зависящая от отказа, P{Е} — вероятность независимого отказа Е, P{Ed} — вероятность независимого отказа.

• 3)    Показатель чувствительности параметра X может быть выражен как производная функции безопасности относительно X:

  S (X ) =

  
  

  dPSI (X ) dX