Анализирующие свойства электростатического ионного ускороителя

В настоящее время времяпролетная масс-спектрометрия стала незаменимым инструментом исследования во многих областях современной науки, таких как молекулярная биология, протеомика, медицина и др. Разработка и создание вре-мяпролетных масс-спектрометров стало одним из важных направлений современного научного приборостроения. Как известно, высокие значения разрешающей способности и чувствительности в современных времяпролетных масс-спектрометрах типа масс-рефлектрон достигаются путем применения в их ионно-оптических схемах специальных устройств — ионных рефлекторов различных модификаций [1, 2]. Приборы простой конструкции, не содержащие ионных рефлекторов, например [3], имеют сравнительно низкие разрешающую способность и чувствительность. Это обусловлено главным образом тем, что для формирования ионных пакетов используются простые однородные электрические поля, образованные в ускорительном промежутке между плоскими мелкоструктурными сетками. Такие поля не могут обеспечить высококачественную пространственную и времяпролетную фокусировку ионных пакетов на плоскость детектора, а использование мелкоструктурных сеток существенно усугубляет ситуацию. В настоящей работе исследуется ионная оптика времяпролетного масс-спектрометра, в котором высокие значения разрешающей способности и чувствительности могут быть достигнуты без применения ионного рефлектора — путем более полного использования свойств пространственной и времяпролетной фокусировки ионных пакетов в неоднородном электростатическом поле ионного ускорителя.

АНАЛИЗ ВРЕМЯПРОЛЕТНЫХ АБЕРРАЦИЙ

Рассмотрим простой времяпролетный масс-спектрометр (см. рисунок) содержащий электростатический ускоритель ионных пакетов, выполненный в виде системы внешних по отношению к ионному пучку электродов 1–4 с общей осью z вращательной симметрии, источник ионов И, детектор ионов D и бесполевое дрейфовое пространство, определяемое расстоянием между выходной плоскостью 5 ускорителя и входной плоскостью Z D детектора D ионов.

В цилиндрической системе координат ( r,у,z ) источник ионов представляет собой насыщенную ионами область ( r ₀ , z 0 ) в виде диска с радиусом

R >  r и толщиной К | -— h _n<  z _n< — h _n | (область 0 0 0 2 0 0 2 ⁰

экстракции ионов, образованных одним из известных способов ионизации). Начало координат совместим с центральной точкой этой области ( r ₀ = z 0 = 0 ) . В определенные моменты времени эту область пронизывает ускоряющее электростатическое поле, которое извлекает из нее ионы, ускоряет их, формирует короткий по длительности пакет и выталкивает пакет ускоренных ионов в свободное от поля дрейфовое пространство для последующего времяпролетного анализа. Примем, что потенциал ускоряющего поля ф = ф ( r , z ) описывается симметричной относительно плоскости z = 0 функцией координат

ф ( 0, z ) = Ф ( z ) = -Ф ( - z ) , Ф 0 ² n ) = 0, (1) (0 <  n <^), Ф 0 * 0.

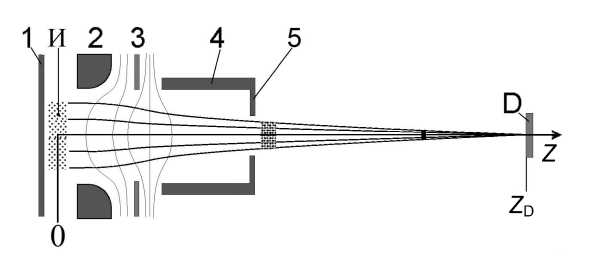
Ионно-оптическая схема времяпролетного масс-спектрометра.

1 — выталкивающий электрод; 2, 3, 4 — система фокусирующих электродов

Это условие, в общем случае необязательное, обычно используется при расчете импульсных ионных ускорителей. В этом случае выталкивающий электрод 1 имеет вид плоскости и формирует вытягивающее электрическое поле в области источника ионов, близкое к однородному полю, что несколько упрощает расчет и практическую реализацию системы.

Необходимо отметить, что в процессе ускорения пакета ионов (с зарядами e и массами m ) к моменту его инжекции в пространство дрейфа, ионы в пакете приобретают разные энергии вследствие двух физически разных причин.

Во-первых, ионы стартуют с разными начальными значениями продольной скорости частиц Z 0 , что приводит к соответствующему разбросу кинетических энергий ионов в пакете, равному

^z 2 ^{+ r 2} = m ( ф ( r , z ) ^— ф ( r „ , z 0 ) + ^£ ) .

Введем обозначение:

m .

£ = — z

2 e

Во-вторых, ионы стартуют из разных точек об-

ласти экстракции при разных начальных значени-

ях z ₀ , и в результате ускорения пакета они в пространстве дрейфа приобретают дополнительный разброс кинетических энергий, равный £ _ф - - z 0 Ф 0 .

Обычно начальный разброс кинетических энергий ионов ε является малой величиной по сравнению с дополнительным разбросом энергий £ _ф , приобретаемым в процессе ускорения пакета ( £ ^ £ _ф| ). Однако, его нельзя исключить из рассмотрения, поскольку именно начальный разброс кинетических энергий ионов ε , как будет показано ниже, в конечном итоге определяет предельное разрешение любого времяпролетного масс-спектрометра, в том числе и масс-рефлектрона.

С учетом сказанного напишем закон сохранения энергии заряженной частицы в виде

^—ф ( ^z 0 , r 0 ) + ^£ = ^—ф ( z , , ^r 0 ) ^{- —ф} 0 ^z 0 ^{+ £} = ^—ф 0 z , ,

откуда получим:

z , = z 0

ε

—

Ф0

.

Рассчитаем время пролета t частицы от точки ее старта ( r ₀, z ₀ ) до референсной плоскости z = z 1 = const, расположенной в дрейфовом пространстве. С учетом равенств (1)–(3) напишем цепочку следующих друг за другом уравнений:

t =

z1    x/1 + r ,2dz    = z0 7ф(z,r) —ф0z£

= f m" z ^£   V1 + r '²dz

’ ^2e = 0   ф ( ^z , ^r ) ^—ф 0 ^z £

m^  V1 + r '²dz   _

’ ^2е=.^ф(,^z , ^r ) ^—ф 0 ^z _E

/

к z ^£

к

■   V1 + r '²d z     =

V ^ ^{( z} , ^{r ) —ф} 0 ^z , _v

^—■ z ^£          1 + r '²d z

0 7 ^ ( z ⁺ z £ , r ) ^—ф 0 z

к ⁰

X

^£ 7

+ r ^,2d z   z_£ 4 1 + r

—

^Ф( 1 + q )   7^ф 1 — ^ф 0 z , /

Здесь Ф 1 = ф ( z 1 , r 1 ) = const — постоянный потенциал дрейфового пространства, а q — малая ве-

личина, равная

q =

ф^ ( ф ⁽ z + Z _E , r ^)-ф 0 Z _E ) ^- 1 ■

Ф'-Ф 0 ф

Ф"[ 2

z +--- z s 2Ф( s

+ ...

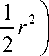
пролетной фокусировки первого порядка z = Z D длительность A t _D пакета ионов определенной массы m описывается суммарной времяпролет-ной аберрацией второго порядка малости относительно разброса энергий вылета ионов ^s ф ^{— — z} 0 ^Ф 0 :

Учтем, что для центральной частицы ( r₀ = z 0 = 0 ) , движущейся вдоль оси z c s = 0, время пролета до референсной плоскости z = z ₁

равно

a t d =^2 m y( ⁼ " ^K -⁽²'+ ^r « K- ' ) ■ r , <  R 0   - 0.5 h 0 <  z 0 <  0.5 h 0 ,

T =

m ^{z 1}    d z

N ² e 0 ^ Ф ( z )

Далее, используя равенства (4)–(5), запишем разность величин T - 1 = A t . Удержав в этом выражении величины не выше второго порядка малости, получим равенство, определяющее время-пролетные аберрации ионного пакета в дрейфовом пространстве в зависимости от его положения z = z_x на оси системы:

A t = T -1 =—.

ФИ e 0

2 е ф ( z s K"" ( z i ) + z 2 K? ( z i ) + Г о ^{2 K}^ ( z i ) ) .

УСЛОВИЯ ФОКУСИРОВКИ ИОННОГО ПАКЕТА

Сначала положим в равенстве (7) s = 0 и рассмотрим времяпролетные аберрации в случае равенства нулю начального разброса кинетических энергий частиц. В этом случае из выражений (4), (5) и (7) следует, что в пространстве дрейфа существует плоскость, в которой имеет место время-пролетная фокусировка ионных пакетов первого порядка по отношению к разбросу энергий вылета частиц s _Ф - - z ₀ Ф 0 . Положение этой плоскости z = Z D определяется равенством K ^¹ ( Z D ) = 0, разрешив которое относительно величины Z _D , найдем

Z

=+

D Ф0

j[^- Аф ) ²

J ф'     I ф j

0 <^Ф 0 УУ ^{Ф y}

^

+ 1 d z .

У

Здесь и в дальнейшем знак да в верхнем пределе интегралов означает, что интегрирование ведется до произвольной точки в свободном от поля пространстве, где подынтегральные выражения становятся равными нулю. В плоскости время-

где K_z ⁽²⁾ и K_r ⁽²⁾ — аберрационные коэффициенты

второго порядка:

K ⁽²⁾ =¹ z 4

[Ф+ v 1

Z _D

J

[ Ф’

Ф

V

-

У

K^ =

Z _D

1 Г [ Ф 2

-  --P + P

2 0 V 4 Ф

d z .

d z , (10)

Здесь p = p ( z ) — частное решение параксиального уравнения

4 Ф p " + 2 Ф‘ p ' + Ф" р = 0

с граничными условиями

p (0) = p 0 = 1, p 0 = 0, p ( Z d ) = 0. (12)

При совместном выполнении условий (8) и (12) обеспечивается одновременная пространственная и времяпролетная фокусировка первого порядка ионных пакетов на входную плоскость z = Z D детектора ионов D. При этом, как видно из выражения (9), коэффициент K_z ⁽²⁾ определяет рассеяние регистрируемых ионов по ширине пакета в направлении его движения, а коэффициент K_r ⁽²⁾ — искривление переднего фронта ионного пакета.

Отметим, что коэффициенты времяпролетных аберраций K_z ⁽²⁾ и K_r ⁽²⁾ легко могут быть сведены к нулю специальным выбором осевого распределения электростатического поля Ф = Ф ( z ) . Это вытекает из следующих соображений. Вследствие обратимости траекторий заряженных частиц в электростатических полях рассматриваемая ионно-оптическая система (рисунок) по своему фокусирующему воздействию на пакеты ионов подобна фокусирующему воздействию осесимметричного электростатического ионного зеркала на пакеты отраженных им ионов. Это обстоятельство, позволяет при расчете рассматриваемого времяпро-летного масс-спектрометра использовать (естественно, с соответствующими модификациями) известные многочисленные расчетные данные [4–7]

о пространственных и времяпролетных характеристиках ионных зеркал. Из этих данных, в частности, следует, что существуют сравнительно простые четырехэлектродные системы [6], в которых коэффициент времяпролетной хроматической аберрации может быть сведен к нулю вплоть до величин четвертого порядка малости относительно разброса энергий £Ф, приобретаемого в процессе ускорения пакета. В таких системах одновременно с пространственной фокусировкой первого порядка может быть достигнута время-пролетная фокусировка по энергии четвертого порядка, а времяпролетная хроматическая аберрация AtD определяется малой величиной лишь пя того порядка относительно величины £ф

Тогда предельное разрешение масс-спектрометра R , связанное с величиной ε , будет

R -

D m

A t

- R о

Здесь R ₀ — безразмерный коэффициент, характеризующий предельное разрешение прибора, равный

Ro -1 02

1I: J

2 Ф 1 ¹ V

(Ф0

VФ0 V

- 1

A

d z . (17)

7 7

A t _D

- х<«

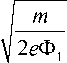
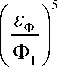
С учетом сказанного можно утверждать, что начальный разброс кинетических энергий ε , несмотря на его сравнительно малую величину £ ^ £ _ф|, оказывает наибольшее влияние на величину времяпролетной аберрации A t . Как следует из уравнения (7), в случае равенства нулю время-пролетных хроматических аберраций, связанных с коэффициентами K_z ⁽²⁾ и K_r ⁽²⁾ , суммарная времяпро-летная хроматическая аберрация пакета определяется равенством

При выводе последнего соотношения использованы равенства (6), (8), (14) и (15).

Для упрощения вычислительных процедур, а также для решения задач оптимального синтеза системы целесообразно ввести вместо перемен-

Ф0

ной z безразмерную переменную x - —- z . Рас-

Ф1

A t = —

Ф0

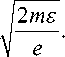
пределение потенциала на оси системы также целесообразно характеризовать безразмерной функ цией переменной x: U (x)-—Ф — x . В без-v ' Ф1 £ф0 7

размерных переменных основные формулы (8) и (17), характеризующие линейный размер масс-спектрометра и величину его предельного разрешения, упрощаются и принимают следующий вид:

Из последнего равенства видно, что величина времяпролетной хроматической аберрации, связанная с начальным разбросом кинетических энергий ε , не зависит от выбора положения z = Z _D плоскости детектирования ионных пакетов.

xD

со

- ² + 1

L .   .3 A

( U '-1 ) U ² + 1 d x ,

V              7

R -1 +1J(1 - и)(u' -1)и~2dx.

ПРЕДЕЛЬНОЕ РАЗРЕШЕНИЕ

Определим предельное разрешение масс-спектрометра, связанное только с наличием разброса начальных кинетических энергий ионов £ ^ 0. Времяпролетную дисперсию прибора найдем, используя равенство (6), в котором положим z = Z d :

D

m

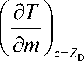
= ¹ T_{z z}

2 ^{z - Z} D

1 / m ^Z D ^D    Ф.

¹ d z .

2P e Ф 1 ^Jo Wz )

Штрихами обозначено дифференцирование функции и ( x ) по безразмерной переменной x .

Из выражений (18) видно, что, варьируя осевым распределением поля U - U ( x ) , можно по-разному влиять как на линейный размер ионно-оптического тракта, так и на величину разрешающей способности рассматриваемого масс-спектрометра. Это обстоятельство дает достаточно широкие возможности выбора конкретных систем и, в частности, позволяет поставить задачу оптимального синтеза вре-мяпролетного масс-спектрометра по критерию наибольшей величины отношения предельного разрешения к протяженности ионно-оптического тракта прибора.

ЗАКЛЮЧЕНИЕ

В заключение отметим, что описанный время-пролетный масс-спектрометр несложен в исполнении, его детали и узлы технологичны. В этом приборе электростатический ускоритель осуществляет пространственную и времяпролетную фокусировку ионных пакетов непосредственно на входную плоскость детектора ионов. При этом для достижения высокой разрешающей способности и чувствительности нет необходимости в применении дополнительного устройства — рефлектора ионов, что значительно упрощает конструкцию прибора, уменьшает влияние аберраций, связанных с конструктивными погрешностями и упрощает настройку и юстировку прибора в целом.

Отметим также, что проведенное рассмотрение пространственно-времяпролетной фокусировки выполнено для систем с вращательной симметрией, однако его легко распространить и на системы другого типа симметрии, в частности, на планарные системы [8], естественно, с соответствующими модификациями.