Аналог интеграла Рэлея-Зоммерфельда для анизотропной и гиротропной сред

Всё больший интерес с практической точки зрения вызывают оптические устройства, позволяющие преобразовывать свойства электромагнитного излучения. Среди наиболее просто реализуемых – поляризационные и модовые преобразования.

Распространение лазерных мод высокого порядка в среде с сильной анизотропией приводит к сложным поляризационно-модовым преобразованиям [1 –4]. Причём для анализа таких явлений часто используется параксиальная модель распространения [5,6].

Заметим, что взаимодействие поляризации и пространственного распределения электромагнитного поля происходит также в изотропной среде в непараксиальном режиме, в частности, при острой фокусировке [7–9].

Непараксиальный режим в анизотропной среде позволяет обнаружить более тонкие эффекты [10 – 13]. Как правило, в этом случае используется разложение по плоским волнам [14 – 16], которое в общем случае при численной реализации требует четверного интегрирования по пространственным и спектральным переменным. Для уменьшения времени расчёта двойной интеграл по спектральным переменным можно асимптотически вычислить методом стационарной фазы [17]. Причём такая асимптотика позволяет получать достаточно точные результаты уже на расстоянии нескольких длин волн [18].

В данной работе рассмотрен непараксиальный интегральный метод расчёта распространения электромагнитных волн в анизотропных и гиро-тропных средах. Интегральное выражение для сред с разделимостью продольных и поперечных компонент записано в завершённой аналитической форме. В частных случаях данное интегральное преобразование сведено к аналогу интеграла Рэлея–Зоммерфельда.

1. Монохроматическое поле в анизотропной среде

Уравнения Максвелла для области, свободной от источников, записываются в виде (в системе СГС)

^V B = 0,

V D = 0.

В однородной анизотропной среде, описываемой тензорами диэлектрической и магнитной проницаемости

ε=

⁸ xx

⁸ yx

г

^ zx

ε xy ε yy ε zy

8 xz zz j

,

(2а)

Ц xx

Д = Ц yx

, Ц zx

xy

yy

)

xz

yz

,

(2б)

^µ zy

Ц zz J

имеется следующая зависимость:

B = ц H ,

D = e E .

Для монохроматического поля

E ( x , y , z , t ) = E ( x , y , z )exp ( - i ω t ) , H ( x , y , z , t ) = H ( x , y , z )exp ( - i ω t ) .

уравнения Максвелла (1) –(3) принимают следующий вид:

Vx E = ik ₀jI H , Vx H = - ik ₀ e E , V ( p i H ) = 0, ^V ( ^e E ) = 0,

где k ₀ = ω / c = 2 π / λ ₀ , λ ₀ – длина волны в вакууме.

Из первых двух уравнений системы (5) получаем 6 уравнений для 6 компонент:

^∂ _∂ ^E _z ^x = ^∂ _∂ ^E _x ^z + ik 0 ( µ yx H x + µ yy H y +µ yz H z ) ,

∂ E y ∂ z

_{∂ y} - ik 0 ( µ xx H x +µ xy H y +µ xz H z ) ,

Систему (6) можно свести к 4 уравнениям для 4 поперечных компонент. При использовании разложения по плоским волнам

H z =

-

i

k ₀ µ _zz

∂ E y ∂ x

-

∂ H x ∂ z

∂ H y ∂ z

∂ H z ∂ x

^d E ^L | - —( Н zx H x +Н zy H y ) , _∂ y     _µ zx x zy y

^J zz                      (6)

- ik ₀ ( ε _yxE_x +ε _yyE_y +ε _yzE_z ) ,

= ^z + ik ε E + ε E + ε E

_∂          0 xx x xy y xz z ,

i fdHy _^Hl z    k0 ezz I dx      dy I e ( zx x zy y).

0 zz                              zz

αε βµ

-

αβ

--

ε _zz     µ _zz

ε _zz

yx

-

ε zz

^µ zz

ε zz

^µ zz

β ²

-   + µ _xx

ε zz

αβ

+ε µ _zz

yx

-

εε yz zx

-

β ²

-

^µ zz

ε

xx

ε _zz

α ²

+ε µ _zz

yy

-

εε yz zy

ε _zz

εε

₊ xz zx ε zz

αβ

--

^µ zz

ε

xy

₊ ε xz ε zy ε zz

∞

F ( x , y , z ) = j| f ( а , в ) х

-∞ х exp |^ ik0 (аж + вy + Y(а, в) z)] dа dв

эта система в пространственно-частотном представлении будет иметь следующий вид:

+

-

^µ yz ^µ zx

µ _zz

^µ xz ^µ zx

^µ zz

γ + α^{µ zx} + ^βε ^yz µ _zz ε _zz

-

α ²

ε _zz

-

µ yy +

^µ yz ^µ zy

µ _zz

^µ zz

ε zz

где e_{x , y} ( α , β ) , h_{x , y} ( α , β ) – коэффициенты разложе-

ния (7) поперечных магнитного поля.

Далее систему (8)

компонент электрического и

можно решить численно, оп-

ределяя собственные значения γ _j ( α , β ) , j = 1,4 из равенства нулю определителя матрицы. Линейная комбинация 4 поперечных собственных векторов обеспечивает общее решение задачи распространения в среде, заданной тензорами (2). Продольные компоненты выражаются через поперечные из (5).

2. Интегральный оператор распространения электромагнитных волн в анизотропной и гиротропной среде с разделимостью компонент

Рассмотрим тензорами:

среду, описываемую следующими

ё =

ε xx

<

ε _yx 0

ε _xy ε yy 0

,

(9а)

µ xx

Заметим,

^µ xy ^µ yy 0

что

^е zz у

.

(9б)

Н zz J в общем случае значения в (9) мо-

гут быть комплексными и ε ≠ ε , µ ≠ µ , что xy yx xy yx

позволяет описывать различные типы сред, в том числе гиротропную среду [19].

В этом случае система (8) разбивается на 2 подсистемы [20]:

αβ

+µ ε zz

-

^µ xz ^µ zy

xy

^µ zz

αµ αε zy yz

-

µ _zz     ε _zz

^βµ zy   αε

γ +     + ^xz

^µ zz     ε zz

γ e _⊥ = Ah _⊥ , γ h ⊥ = Be ⊥ ,

где e _⊥

A =

B =

e x ^(а , ^в) e y ( а , в ) *Р ) ( h y ( а , в ) J

= 0,

e x ^{( а} , ^{в )} 1 h = f h x ^{( а} , ^{в )} 1

ey(а,в) J’ ± (hy(а,в) J’ а2 i

ε _zz αβ

Г ав — + Н

ε _zz β ²

yx

-

,

-

I ^е zz г ав

xx

--

ε _zz

--

ε

α ²

Н zz ■

-jl+e l Н zz

yx

xx

-

^µ zz

Н е yy

ав

^+е xy

^Н zz      у

.

Подставляя в (10) первое уравнение во

второе,

получим уравнение относительно только поперечных компонент электрического поля

из которого, обозначая M = AB , следует уравнение на собственные значения:

M ₁₁ -γ ²

M 21 Решением

выражения:

γ 1,2 ⁼

где

M 12 M ₂₂ -γ ²

= 0.

уравнения (12) являются следующие

( M 11 + M 22 ) ± ( M 11 - M 22 ) ² + 4 M 12 M 21

2                     ,(13)

M 11 =       [- ( ар + е _zz ц yx )( ар + ц _zz г yx ) ⁺ ( ^{а 2} - г _zz ц )( р ^{2 -}ц _zz г x ) ^] ,

Е zz Ц zzL г zz Ц zzL'

г zz Ц zzL г zz Ц zzL'

Будем далее рассматривать только положительные значения собственных значений (13), которые соответствуют распространению волн в положительном направлении оптической оси (вправо).

Из уравнения (11) получается связь поперечных электрических компонент для каждого собственного значения, в частности:

^M 12

При этом один из векторов в паре выбирается произвольно, например, можно положить [20]:

ejx (°, в) = M12, ejy (а,Р) = у2(а,в)-Mп.

(16а)

Также можно использовать другое соотношение:

(16б)

или суперпозиции полученных векторов.

Из второго уравнения (10) получаем выражение для поперечных магнитных компонент, а из уравнений (5) - для продольных компоненты электромагнитной волны ( j = 1,2):

h jx ( ^а , ^в ) =

h jy ( а , в ) =

Ц zz Y j ( ^{а , в} )

,

^Е zz Y j ( ^{a , в} ) в e jx ( а , в ) -а e jy ( а , в )

,

Ц zz

■

Две волны в (15)-(17) соответствуют обыкновенной ( /' =1) и необыкновенной ( /' =2) волнам.

Следуя работе [20], рассмотрим общее решение, используя линейную комбинацию поперечных компонент электрического поля:

Из (18) и (19) получаем:

Г c ( а , в ) ) =

( c 2 ( а , в ) 7

P x ( а , в ) ) = P y ( а , в ) 7

T¹ Г P x ( а , в )⁷

IPy (а,в)7’

= c ( ^а , ^в )

Г e x ( а , в ) 7

I e y ( а , в ) 7

+ c 2 ( а , в )

где функции c ( а , в ) , c ₂ ( а , в ) подлежат определению.

Получить значение этих функций можно из заданного распределения поперечных компонент электрического вектора в плоскости z=0:

где f Px (а,в)7 =

I P y ( а , в ) ⁷

1 fCEE x ⁽ x , y ^{,0) 7} Г Z Г О 11 д д ‘I⁷ И( E , ( x , y ,0) 7 ^СХР<" i ^{k [а} * ^{+ в} y В d x d y .

+

( e 2 y ( а , в )

(19) exp { ik [ o x + в y ] } О а О в .

Таким образом,

Г c ( ^а , ^в ) 7 = ( c 2 ( а , в ) ⁷

= XГ e 2 y ( а , в ) P x ( а , в ) А ( e x ( ^а , ^в ) P y ( ^а , ^в )

во

2x e1 y

^{- e} 1 y

_; ( а , в ) P y ( а , в ) ) . ( ^а , ^в ) P x ( ^а , ^в ) 7 , ( ^а , ^в ) e 2 x ( ^а , ^в ) ■

С учётом полученных выше выражений интегральный оператор распространения записывается следующим образом:

( E ( u , v , z ) j =

V H ( u , v , z ) J

x exp | ikz Y 1 ( a , в ) ] + c 2 ( a , в )

x e _{2 ±} ( a , в ) exp [ ikz Y 2 ( a , в ) ] } х

X exp | ik ( a u + в v ) ] d a d e ,

где

A

G e ( a , в ) =

a£ +в£„ xx yx

^a£ xy ^+в£ yy

,

V

j = 1,2,

G h ( a , в )

£ zz Y j ( a , в )	£ zz Y j ( a , в ) J
( aв + £ yx ц zz	a 2 -£ yy ц zz
Y j -( a , в )	Y j ( a , в )
-в 2 +£ xx ц zz	aв+£ xy ц zz

A

ц zz

Y j -( a , в )

-в

Y j ( a , в ) a

V

J

E ( u , v , z )

H ( u , v , z )

X

+

= ^ffff

A- j = 1

( e j ( a , в ) j v h j ( a , в ) j

X

| w j ( a , в ) T E _± ( x , y ,0) ] exp { ik |a ( u - x ) +     (28)

■ в( v - y ) + Y j ( a , в ) z ] } d a d в d x d y .

Внутренний интеграл можно вычислить методом стационарной фазы [17].

3. Аналог интеграла Рэлея–Зоммерфельда для анизотропной среды

Рассмотрим наличие только диэлектрической анизотропии, т.е. ц xy = ц yx = ⁰ , ц xx = ц yy = ц zz = ц . Заметим, что для анизотропных кристаллов тензоры вида (9 а ) имеют действительные значения и должны удовлетворять условию симметрии: £ x _y = £ _y x . Кроме

того, такие виду

ё =

V

^£ 1

тензоры приводятся к диагональному

^£ 2

^£ 3 J

поворотом на угол ^ [21] tan2 y=    2 ^{£ xy}   ,

( ^£ yy ^-£ xx )

^£ 1

( ^£ xx ^+£ yy )      £ xy

^£ 2 =

( ^£ xx ^{+ £} yy 2

sin 2y ’

) ,     ^£ xy

+         , sm2y

j = 1,2.

Выражения (23)-(25) можно виде:

записать

в

другом

£ = £„

3 zz

.

E ( u , v , z ) j = 2

H ( u , v , z ) J "  £ JJ

⁽ e j ( a , в ) V h j ( a , в ) J

X

X|^Wj(a, в)T P±(a, в)]X xexp|ik(au + вv + Yj (a, в)z)]dadв, где wj-(a,в)T P±(a,в) = Cj (a,в), P±(a,в) тральный вектор из (21),

Wi (a,в)T = A-1 (e2y (a,в),-e2x (a,в)), w2 (a,в)T =A-1 (-e1 y (a,в),e1 x (a,в)),

Для тензора вида (29) при изотропной магнитной проницаемости элементы матрицы M примут следующий вид:

M 11 =£ 1 ц-1 в ² + a ² — I ,

V ^£ 3 J

M ₁₂ = aв 1 1 -^ 2 I , V ^£ 3 J

спек-

( e j ( a , в ) )

– собственные (поляризационные) век-

Vhj(a, в) J тора, определённые в (17).

Подставляя в (26) выражение (21) и меняя порядок интегрирования, получим:

M ₂₁ = aв1 1 -■^£l I , V ^£ 3 J

M ₂₂ = £ ₂ ц-1 a ² + в ² —

V         ^£ 3 J

Собственные значения:

2       11      2( 1     £i

Y 22 =-^-a ² 1 + —

^1,2 2 I V £ 3

e ² | i +-

V ^£3.

.

где

T. = а ² 1 1 -^- I + в ² 1 1

_ V ^Е з ) V

₽ 12 52-1 Ез )

+

а ²

Выражения для поперечных электрических векторов:

I Е, I е (а,в) = ав| 1 —2 I,

V Е з )

(34а)

e jy ( а , в ) = У 2 ( а , в ) +1 в 2 + а ² — I -Е 1 ц V        Е _з )

или

f         Е. I e,x (а,в) = ав| 1 —L I, V Ез )

(34б)

е ejy

Для остальных компонент:

h jx ( ^а , Р ) =

-ав e ,x ( а , в ) + ( а²-^ ) e jy ( а , в )

hy (а,в) =

ЦуДа , в )

- ( в ² - цр ) e ,x ( а , в ) + ав e jy ( а , в )

,

e jz ( ^а , ^в ) =

ЦуДа , в ) ар е ,^ ( а , в ) + в^ 2 e jy ( а , в )

,

h jz ( ^а , Р ) =

е

Е з 7 _у -( а , в ) в e jx ( а , в ) -а e jy ( а , в )

,

Ц

.

Заметим, что выражение для собственных значений (32) значительно упростится, если под корнем можно выделить полный квадрат, а также если M ₁₂ = 0 или M ₂₁ = 0. Такие ситуации возникают, когда анизотропная среда является одноосной, т.е. два из трёх значений диэлектрической проницаемости совпадают.

В общем же случае применить метод стационарной фазы к выражению (32) затруднительно, однако в параксиальном приближении, т.е. когда а , в малы, также можно получить более простой аналитический вид.

Во всех этих случаях собственные значения сводятся к виду

у ( а , в , d, s, t ) = 4d - s а ² - t в 2 ,

где d, s, t – константы, зависящие от значений тензора (30).

Таким образом, вид для быстроосциллирующего члена в (29):

exp { ik [а p + в q + z^d - s а ² - t в ² J } ,

где p = u - x , q = v - y .

Из уравнения

—[ а p + в q + z^d - s а ² - t в ² 1 = 0

[ дв L '                J

получаем выражение для стационарной точки

r в c

tp2d s (tp2 + sq2 + stz2) sq2d

t (tp2 + sq2 + stz2)

Тогда внутренний интеграл в (28) можно приближённо заменить подынтегральным выражением в стационарной точке [17]:

2 n

x

где

( t ( u - x ) 2 + s ( v - y ) 2 + stz ² )

stdz ²

.

В стационарной точке exp{ik[аcp + вcq + z^d - sаc2 -1вc2 ]} =

= exp

² + sq ² + stz²

.

Тогда выражение (28) можно записать похожем на интеграл Рэлея–Зоммерфельда:

f E ( u , v , z ) I = 2 n z Л rr

V H ( u , v , z ) )        ^j = 1

e j^jc , в е ) V в ( а,, в, ) )

x

в

виде,

^x[ w j ^^ c ,в- c ) ^{T E} ± ⁽ x , y ^{,0) ]x}

x

ik ——R, Г dx d y , ^j

s j t j

где

R j = Jt j ( u - x ) 2 + s j ( v - y ) ² + s j t j z² ,            (44)

в.

d j t j ( u - x ) s_j    R_j

$ ^dj^sj ^{( v - y} )

t j R j

Рассмотрим конкретные частные случаи и определим для них параметры выражения (43).

3.1. Одноосный кристалл, ось которого направлена вдоль оси распространения Oz

В этом случае 8 1 =8 2 =8 0 , 8₃=8 e . Такая конфигурация рассматривалась в [22], однако непараксиаль-ность учитывалась как дополнительные члены к параксиальному оператору распространения. В нашей работе непараксиальность сразу учитывается в выражении (43), представляющем собой аналог интеграла Рэлея-Зоммерфельда.

Элементы матрицы M :

I                е I

M 11 = е о ц-I в ² + а ²- ° - I ,

I        ^е e )

_п L е

M ₁₂ = M ₂₁ = ав| 1 - —

I ^е e )

M ₂₂ = е _о ц-I а ² + в ² — I            е_

Собственные значения:

Y 1 ( а , в ) = ^ е о ц- ( а ² + в ² ) ,

Y 2 ( а , в ) =

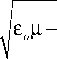
—( а ² + ^е e

в ² ) .

Первое собственное число соответствует обыкновенной волне, а второе - необыкновенной.

Первая пара собственных векторов:

e 1 X

( а , в ) = ав I 1 -

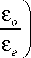
„ I е e у (а,в) = -а I 1 —-

I е_

которая с учётом общих множителей может быть записана в виде:

e 1 X =в , e 1 у = ^-а .

Аналогично для второй пары:

e 2 x ^а , e 2 у = ^в .

Используя (35), получим остальные векторы:

(е Г e 1 X	I вц I
e 1 у	-ац
e 1 z       1	0 . .
h 1 X "ц	аY 1 ( а , в )
h 1 у	вY 1 ( а , в )
V h 1 z )	V - ( а 2 +в 2 ) у

Ге Г e 2 X

e2 у e2 z

h h

⁽2 х

¹2 у

Y 2 ( а , в )

' ^аY 2 ( ^а , ^в )

вY 2 ( а , в )

А

^ ( а ² + в ² ) ^е e

ае -

.

)

Из (50) видно, что обыкновенная волна является

TE-волной ( e 1 _z = 0), а необыкновенная - ТМ-волной

( h 2 _г = 0).

Векторы (27) принимают следующий вид: W 1 ( а , в ) T = ( а ² + в ² ) ¹ ( в , -а ) , w 2 ( а , в ) T = ( а ² + в ² ) ¹ ( а , в ) .

Т.к. d 1 = d ₂ = е _о ц , 5 1 = t 1 = 1, 5 ₂ = t ₂ = е _о / е e , то ста

ционарные точки в (43) будут иметь следующий вид:

1------------ ас хе о ц в. = 7^

( и - X ) R j ⁽ v ^- у ) R j

где

R = V ⁽ u ^{- X )2} + ⁽ v ^- у ⁾² + ^{z 2} ,

R ₂ = р ( и - X ) ² + ( v - у ) ² +^е ° z ² .

\ е eV                        е e

3.2. Одноосный кристалл, ось которого направлена перпендикулярно оси распространения и совпадает с осью Oy

В этом случае е 1 = е ₃ = е _о , е ₂ = е _e . Такая конфи

гурация рассмотрена в [23], однако непараксиальный интегральный оператор распространения не был выписан.

Элементы матрицы M :

M 11 =е о ц-а ² -в ² ,

M ₁₂ = ав I 1 -— I , I ^е о )

M 21 = 0,

M ₂₂ = е _e ц-а ² -^ e ^-. е _о

Собственные значения:

Y 1 ( а , в ) = 7 е о ц-а ² -в ² ,

Y 2 ( а , в ) = /е e ц-а ² -^ в ² .

Первая пара собственных векторов:

в 1 x ( а , в ) = авf 1 -^ e ¹ , \ ^е о )

6 1 у ( а , в ) = 0

показывает, что теперь ось кристалла направлена вдоль оси Оу , и разделения на обычные TE- и TM-моды не произойдёт.

Учитывая равенство нулю электрической у -ком-поненты, можно выбрать первую пару в виде:

elx А в) = 1

e 1 у ^(а , ^в) = ⁰ '

Вторая пара с учётом сокращения общих множителей имеет следующий вид:

e2 x (а, в) = ав, e2 у (а, в) = в2 —£ о .

Используя (35), получим остальные векторы:

T =ц(£1 —£2)

а ² 1 1

£

^£ 3

в ² 1 1 —-

А ^£ 3

, (62)

и тогда собственные значения примут следующий вид:

Y1 ==№

а ² ”- — в ² , £ ₃

Y 2 = ц£ ₂ а ² в 2 —• £ ₃

Из (34) можно получить 2 набора собственных векторов для поперечных электрических компонент:

(е ) e1 x e1 у e1 z

'Ц7 1 ^(а , ^в) '

e1 x (а, в) = 1, e1 у (а, в) = 0, e2 x (а, в) = ав(£3 —

^£ 2 ) ,

А

( I

h 1 h 1 h1:

x

y

I z У

e 2 x e 2 у e 2 z

^h h

¹ 2 x

¹2 у

А h 2 z У

Ц71 (а, в)

ав

—I

—I

ац ав

,

£ оЦ —в2А—в71 (а, в) У

^— ( ^£ о ^{ц —в} 2 ) в? 2 ( а , в ) ^£ o Y 2 ( ^а , ^в ) 0

А^—а£ o

.

У

Векторы (27) принимают следующий вид:

Г ^w 1 ( ^а , ^в ) T = 1, (

Г w 2 ( а , в ) T = 0,

А

ав

(£ оЦ—в2) У’

(”оЦ в ) У

Т.к. d 1 = £ o ц , s 1 = t 1 = 1, d ₂ = £ e ц , 1 ₂ = £ e / £ o , то стационарные точки в (43) иметь следующий вид:

s 2

= 1,

будут

<

( и — x )

^{( v —} у )

R 1

,

,

<

( и — x ) ”r T ^{( v —} у ) R 1

,

,

e2у (а,в) Ц£ (” — £2) + а2 (£3

-

^£ 1 ) ^-в 2 ( ^£ 3

£2 ) ,

остальные векторы можно получить, используя (35).

Векторы (27) имеют следующий вид:

W 1 ( ^а , ^в ) T =

= 1, А

ав ( £3 -

Ц£3 (£1 — £2 ) + а2 (£3 —

w2 (а, в)T =

= 0, А

где

^R 1 = У ⁽ u ^— x ⁾² + ^{( v —} у ⁾² + z ² ,

R 2

।² + — ( v — у ) ² + z ² . ^£ e

Аналогичные результаты можно получить, если ось кристалла будет направлена вдоль оси Ox .

3.3. Двуосная анизотропия в параксиальном приближении

В параксиальном случае в (32):

£2)

£1 ) -в2 (£3

А

£2) У

^У (65)

А

Ц£3 (£1 —£2 ) + а2 (£3 —£1) —в2 (£3

” ) У

Т.к. d 1 = £ 1 Ц , s 1 =£ 1 / £ ₃, t 1 = 1, d ₂ = £ ₂ Ц , s ₂ = 1, t ₂ = £ ₂ / £ ₃, то стационарные точки в (43) записываются следующим образом:

<

R

R 2

( и — x ) R 1 ^{( v —} у ) R 1

,

,

<

£₂Ц ( и — x ) ^а 2 c⁼к— ,

^{( v —} у )

R 2 ’

^{12 + £} 1^{( v —} у ^{)2 + £} 1 z ²,

¹ + £ 3 ( v — у ) + £ 2 z .

Заметим, что, несмотря на параксиальное

при-

ближение, мы сохранили зависимость собственных значений и векторов от пространственных частот вплоть до второй степени. Таким образом, в (43) остаётся условно непараксиальная зависимость расстояний между точками в пространстве вида (67).

4. Интегральные операторы распространения электромагнитных волн в гиротропной среде

Частным случаем сред, описываемых тензорами (9), являются гиротропные среды. В этом случае тензоры имеют следующий вид [19]:

	I e хх  - ig   0 )
- e_	ig e уу 0	,                               (68а)
	0    0 e
	V                  zz J
	I ц„ - iw  0 xx	)
ц _	iW ц уу 0	,                              (686)
	1 0     0 ц zz.
	M" _ 7^-1	- ( ар+ iw e zz )( ар + ig ц zz ) + ( а 2

' zz ^ц zz

где g и w – параметры электрической и магнитной гирации, соответственно.

Гиротропные свойства проявляют некоторые среды (в том числе вода, стекло, алмаз, фосфор), помещённые в постоянное магнитное поле [14].

Используя (14), запишем матрицу M для (68):

-г zz цу, )(р2 -ц zz гхх)],

^г zz ц zz                                                                      ^J

Собственные значения:

Y 1,2    ------- ^Х

^{2 г} zz ц zz

х{ AB2 + A2 B - 2 i ар( we zz + gц zz )± T} },

^{+ 4} ( wg ^г zz ц zz ) ( ^A 1 ^B 2 ^{+ A} 2 ^B 1 ) ^{- 4 A} 2 ^B 2 ( w E zz ) 2 ^-

^{4 A} 1 ^B 1 ( g ц zz ) ^{2 +}

В этом случае собственные значения действительные и соответствуют двум распространяющимся с различными скоростями волнам.

Собственные вектора вычисляются из (73) с использованием (16) и соответствуют эллиптической поляризации.

Так как собственные значения и вектора не зависят от пространственных частот (отсутствует дифракция), то выражение (28) принимает следующий вид:

+4(ар)2 [(A2 - A)(B2

-

где

A 2 = ( ^а 2 ^-ц zz ^E уу ) ,

^B 1 = ( P ^{2 -E} zz ц хх ) ,

^B 2 = ( P ^{2 -}ц zz ^E хх ) .

^Ех ⁽ u , v , ^z ) | _

^Еу ⁽ u , v , ^z ) J

1^ ? e ^ejх )    ( ^Ех ( ^х , у ^,0) )

■ %² ^ Д e jy J w4 Е у ( х , у ,0) J

Х exp (ik уjz )8( u - х, v - у) 8х dу _

Выражение (71) является действительным, а собственные значения (70) – комплексными, что соответствует частично поглощающей среде.

Рассмотрим нормальное падение электромагнитной волны, пренебрегая слагаемыми, содержащими пространственные частоты:

^M 12 - i ( W E уу ⁺ g ц уу ) , M 21 ^- i ( w e хх ⁺ g ц хх ) , ^M 22 ^- ( wg ^{+ г} уу ц хх ) .

I ----------------------2------------------------------------------- 1 ( ⁷⁴ )

1 II e 1 х^е 2 у % Л j ^ ^e 1 у^е 2 у

+ | e 2 х^е1 у ( ^- e 2 у^е 1 у

—p P- I e 1 x e 2 x

I exp (ikY z) + e1 уе2х J

e2xe1x e2ye1x

exp ( ik Y 2 z ) >

E_x ( u , v , 0)

E_y ( u , v ,0)

Для каждой из поперечных электрических компонент происходит свой набег фазы:

^Ех ⁽ u , v , z ) = % 1 Д { ^{[ е} 1 х^е 2 у exp ( ^ik Y 1 z ) ^-

^{- e} 2 х^е1 у exp ( ^ik Y 2 z ) ] ^Ех ⁽ u , v , ^{0) +}

^{+ е} 1 х^е 2 х ^[ exp ( ik Y 2 z ) ^- exp ( ik Y 1 ^z ) ^{] Е}у ⁽ u , v , ⁰⁾ } ,

1                                  (76)

^Еу ⁽ u , v , z ) ^_ % 2 ^ { ^{[ е} 1 х^е 2 у exp ( ^ik Y 2 z ) ^-

^{- е} 2 х^е1 у exp ( ^ik Y 1 ^z ) ] ^Еу ⁽ u , v , ^{0) +}

^{+ е} 1 у^е 2 у ^[ exp ( ^ik Y 1 ^z ) ^- exp ( ik Y 2 z ) ^{] Е}х ⁽ u , v , ⁰⁾ } .

В частном случае, когда e _хх = e _уу , ц _хх = ц _уу , поляризация будет круговой:

Y 2 ^- ( w ⁺ M x- )( g ^{+ e} x- ) , ^{Y 2 -(} w -Ц xx ⁾⁽ g -E xx ) . e ix ( ^a , P ) = 1, e iy ( a , P ) = - i , e 2 x ^(a , P ) ~ 1, e 2 y ( ^a , P ) = i , A = 2 i .

E x ⁽ u,v,z) =

Если предположить, что изначально поле было линейно-поляризовано вдоль оси x , т.е.

E x ( u , v ,0) = i,

Ey (u, v ,0) = 0, то с учётом (82) распределение компонент на различных расстояниях будет выглядеть следующим образом:

E x ^{( u} , ^v , ^z ) =

^^ j r exP ( ^ikE ^e xx M xx ^z ) ^COS

= 2? { - exP ( ik Y i z ) ⁺ exP ( ik Y 2 z^ Ex ⁽ u ’ v ,0) —

- i - exp ( ik Y 2 z ) - exp ( ik Y i z ) ] E y ( u , v ,0) } ,

E y ⁽ u , v , z ) =

^Ey ⁽ u , v , z ) =

= ^-% 2 e ^xP

= 2? { - exP ( ik Y i z ) ⁺ exP ( ik Y 2 z ) ] E y ⁽ u ’ v ^{,0) +}

+ i - exp ( ik Y ₂ z ) - exp ( ik Y _i z ) ] E_x ( u , v ,0) } .

Как видно из выражения (79), на различных расстояниях z поперечные компоненты будут представлять собой различные суперпозиции исходных распределений этих компонент, в том числе могут пе-

реходить друг в друга.

Для наглядности не будем учитывать магнитную гирацию, тогда собственные значения (77), соответ-

ствующие распространяющимся вправо волнам, принимают следующий вид:

Y i = 7M XX V e xx + g ,

^Y 2 ~ V^M xx л) ^e xx ^— g .

При малом значении гирации:

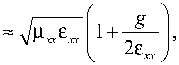
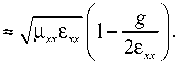
Тогда выражение (79) можно переписать в сле-

дующем виде:

E x ⁽ u , v , z ) = ^r exP ( ^ikE ^e xx M xx z ) ^X

x < cos

k

V

g v^ x r 2л ET xx

)

E x ( u , v ,0) +

+ sin

(

7 g \M xx k  ,— z

2л ET

V V xx 7

E y ( u , v ,0) - ,

^Ey ⁽ u , v , z ) = Z ; exP ( ^ikE ^E xx M xx z ) ^X

X л COS

(

k

V

g v^ x r 2 JEE xx

)

-

E y ( u , v ,0) -

- sin

( k^E xx 2л /e7

V v xx

)

z E x ( u , v ,0) - .

7 J

(

k

V

gjEEE 2 EEE xx

)

z■

( ^ikE ^e xx M xx ^z ) sin

(

k

V

g j^xx 2 ЕЁЕ

)

z

что соответствует повороту плоскости поляризации

на угол

ф= k

g 'j^xx

z

2J E^

xx

в частности, поворот на 45 ° произойдёт на расстоя-

нии, пропорциональном четверти длины волны:

^z 45 °

X Te XX

⁴ g E^ XX ’

а на 90 ° - на расстоянии, пропорциональном поло-

вине длины волны

z 90 °

x E XXE

² g E^ XX

Этот эффект вращения плоскости поляризации при распространении носит название эффекта Фарадея [14, 15, 21].

Заключение

В работе рассмотрен непараксиальный интегральный метод расчёта распространения электромагнитных волн в анизотропных и гиротропных средах. Интегральное выражение для сред с разделимостью продольных и поперечных компонент записано в завершённой аналитической форме. В частных случаях данное интегральное преобразование сведено к аналогу интеграла Рэлея–Зоммерфельда.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, ФЦП «Исследования и разработки по приоритетным направлениям развития научнотехнологического комплекса России на 2007-2013 годы» (Государственный контракт №07.514.11.4055), а также грантов РФФИ 10-07-00109-а, 10-07-00438-а и гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9.