Аналогия перемагничивания обменно-связанной магнитной структуры и изгиба упругого стержня со сжатием

Задачи о перемагничивании магнитомягкого слоя на магнитожесткой подложке с закрепленным и свободным магнитным моментом на поверхностях в постоянном магнитном поле, параллельном плоскости слоя, решались на основе аналогии с потерей устойчивости эйлерова гибкого стержня под действием продольной силы постоянного направления [1]. Уравнение Ландау–Лифшица в статическом случае сводилось к уравнению типа нелинейного маятника и решалось с указанными граничными условиями. В [1] также были найдены распределения магнитного момента и пороги перехода магнитомягкого слоя в веерное состояние в зависимости от магнитного поля, приложен- где ф - угол, зависящий от координаты z по толщине слоя в плоскости этого слоя между вектором намагниченности и осью x, совпадающей с осью легкого намагничивания; a - постоянная обмена ферромагнетика; h = const -внешнее поле; р - константа одноосной анизотропии, Р < 4л.

В [2] было найдено точное решение уравнения (1) в виде дробно-нелинейных комбинаций эллиптических функций, зависящих от одного параметра, определяемого величиной внешнего поля. Эти дробные выражения затем были приближенно представлены в виде полиномов, что позволило найти среднюю по толщине слоя на- ного антипараллельно направлению закрепления.

В работе [2] рассматривалось перемагничивание такого слоя с учетом одноосной анизотропии в плоскости слоя, что привело к уравнению типа нелинейного маят-

магниченность и показать наличие гистерезиса при пе-

ремагничивании. Порог перемагничивания был найден в виде h u + р , где h u = ( n /2)² a / d 2 , здесь d - толщина слоя.

Рассмотрим точное решение этой задачи в виде дроб-

ника с дополнительным членом:

α

' d 2ф'

₄ dz 2 v

+ h sin ф - в sin Ф cos Ф = 0,

но-нелинейных комбинаций эллиптических функций

cos ф =

- 1 + 2 к ² 5 ² - ^ ² 5 ²

2 5 - ( к ² - У )( 1 - к ² 5 ² ) 1 ^sin Ф = —^-------- у^ ----^-—

1 - , 2 5 ²

где 5 ^ sn( Kz I d , к ), здесь функция sn - эллиптический синус Якоби, K ( к ) - полный эллиптический интеграл пер-

вого рода.

Зависимость модуля к эллиптического интеграла K от магнитного поля h определяется уравнением

| | K2 (к)-А(2к02-1) = _,        (4)

πuu эффективное поле однонаправленной анизотропии -

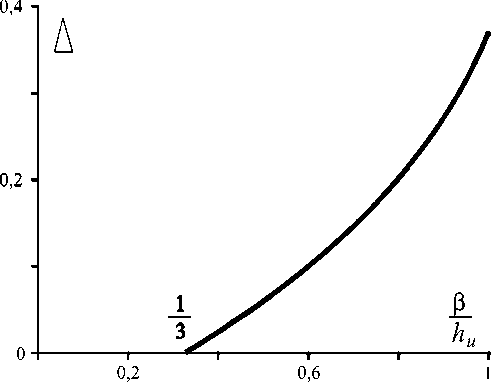
роговым значением постоянного внешнего поля, после которого происходит разворот веера намагниченности, и пороговым значением параметра одноосной анизотропии, при котором начинается раскрытие петли гистерезиса. Правый край этой петли совпадает с пороговым значением постоянного внешнего поля h + 0 , при котором намагниченность меняется скачком. Отметим, что зависимость ширины петли гистерезиса А от величины одноосной анизотропии при значениях 0 I h u > 1 имеет практически линейный характер (рис. 4).

уравнением

hu

2 п i _а_ 2 ) d ’

а параметры - уравнениями

² п к о

, 2 = Р

hu - 2 K (к)_ ’

к о ² =

к ² - у

1 - ,2 '

Выражение (4), в зависимости от величины 0 I h , может иметь минимум по к . Продифференцируем это вы-

ражение по к :

А = hu

4 K ² ( к ) [ E ( к ) + K ( к ) к ² - K ( к )] п² [ - K ( к ) к ² + 2 к ² E ( к ) + K ( к ) - E ( к )] ’

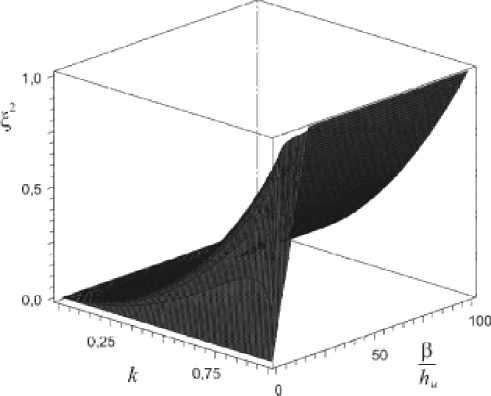
Рис. 1. Зависимость ^ 2 от модуля к и 0 I h u

где E ( к ) - полный эллиптический интеграл второго рода.

Разложение правой части выражения (8) в ряд Тейлора при к ^ 0 дает значение 0 I h u « 1I3.

Подставив к ₀² из (7) в выражение (6), получим явную зависимость с,² от к ² и 0 I h u в виде

, 2 = ^{1 + X} 2

1 - 1 -

А 12

4 X к ²

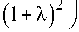
где

х = A I ^п I .                (10)

h 2 K u

Параметр ^ ² при к ² = 0 равен нулю, а при к ² = 1 он имеет максимум, при этом ^ ²< 1 независимо от величины Р ¹ h u ⁽рис. 1).

Построим зависимость внешнего магнитного поля от модуля к и 0 I h u согласно выражению (4) (рис. 2). Эта зависимость при 0 I h u < 1I3 имеет монотонный характер роста, при 0 I h u = 1I3 появляется минимум, а при дальнейшем увеличении 0 I h зависимость становится двухзначной и появляется гистерезис.

Решение (2) усредним по толщине слоя. В результате получим зависимость средней по толщине слоя намагниченности m от постоянного поля h I h , которая обнаруживает гистерезисный характер, начиная с некоторых значений параметра одноосной анизотропии (рис. 3).

Перемагничивание магнитомягкого слоя на магнитожесткой подложке характеризуется двумя порогами: по-

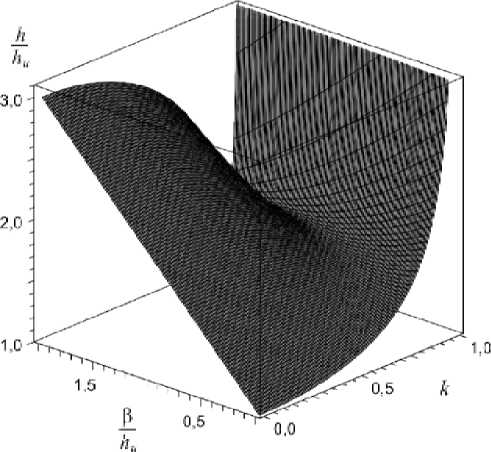
Рис. 2. Зависимость внешнего магнитного поля от модуля к и в I h u

В работах [1; 3; 4] использовался единый статический критерий устойчивости магнитных и упругих систем и была развита нелинейная теория устойчивости этих систем при внешнем воздействии. В частности, в [3] аналитически найдены и систематизированы формы изгиба стержня при различных нагрузках постоянного направления и способах закрепления концов стержня. Полученные решения записаны в едином параметрическом виде и выражены через эллиптические интегралы и функции Якоби, зависящие от одного параметра - модуля эллип-

тических функций, определяемого граничными условиями и внешней действующей силой.

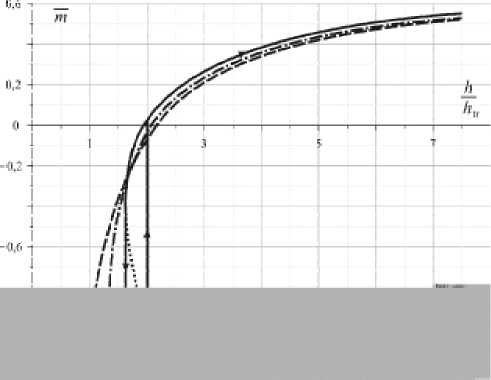
Рис. 3. Зависимость средней намагниченности m от постоянного поля h / h_u (точками показана нефизическая область решения)

вид

Рис. 4. Зависимость ширины петли гистерезиса от величины В / h u

Перемагничивание магнитной системы, рассматриваемое в данной статье, аналогично нелинейному изгибу со сжатием тонкого упругого стержня, закрепленного на одном конце, под действием продольной сосредоточенной нагрузки на свободном конце.

Для описания такого изгиба авторами было получено нелинейное уравнение, аналогичное уравнению (1), для угла наклона касательной в текущей точке к линии стержня с коэффициентами, которые определяются внешней нагрузкой и материальными параметрами стержня:

d ²γ PL ²

—^ +   sin y - dt2 EI

P ² L ² EIE _τ S

sinγcosγ

= 0,

где P - нагрузка; E и Eт - упругие модули; I - момент инерции; L и S - длина и сечение стержня; у - угол наклона касательной в текущей точке к линии стержня; l – длина вдоль линии стержня; t = l / L – безразмерная длина, изменяющаяся от 0 до 1; Pc = (р /2)2 E I / L2 – эйлерова критическая сила. Граничные условия

Y (0) = 0, dYtL 0.           (12)

Уравнение (11) имеет точное аналитическое решение. Построенные зависимости от нагрузки прогиба свободного конца стержня – аналога средней по толщине слоя намагниченности – имеют гистерезисный характер в зависимости от значения безразмерной величины р = (2/ п )² P ² L ² / EIE _т S (рис. 5).

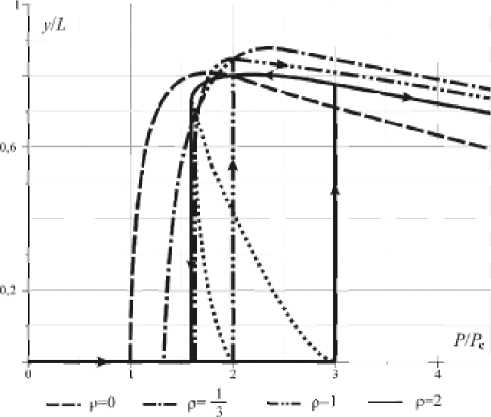
Рис. 5. Зависимость прогиба свободного конца стержня от нагрузки (точками показана нефизическая область)

Система уравнений в параметрической форме, определяющая произвольные точки профиля стержня, имеет

x

L

y

L

tt

J cos y dt - n J cos² Y dt , 00

tt

J sin Y dt - n J cos Y sin Y dt , 00

где параметр n = P / E _T S .

Если положить n = 0, то получим известные выраже- ния для задачи о чистом изгибе тонкого нерастяжимого стержня под действием продольной нагрузки [3].

Изгиб со сжатием упругого стержня характеризуется двумя порогами: пороговым значением продольной сосредоточенной нагрузки, после которого начинается изгиб, и пороговым значением параметра р > 1/3, при котором происходит раскрытие петли гистерезиса. При достижении этого порога упругий стержень под действием продольной нагрузки испытывает прощелкивание.

Таким образом, магнитная и упругая системы имеют одинаковый порог раскрытия петли гистерезиса. При этом при достижении данного порога в магнитной системе под действием поля скачком устанавливается некоторое распределение намагниченности по толщине слоя, а упругий стержень при нагрузке испытывает прощелки-вание.