Analysis of Net Causal Flows in Circuit of Premotor Control during Left Hand’s Movement Readiness State

Published Online February 2011 in MECS

The movement-readiness state defined as a premovement phase, which involved evolvement of cerebral networks from the resting state to movementexecution state, has been studied intensively for years using brain imaging techniques [1-3]. The previous study on monkey in right hand’s movement readiness revealed a circuit of motor control passing through anterior cingulated cortex (ACC), posterior cingulated cortex (PCC), upper precuneus (UPCU), caudate nucleus (CN), cingulated motor area (CMA), left supplementary motor area (LSMA) and left primary sensorimotor area (LS1M1) in turn [4]. The movement-readiness state has been confirmed to involve in motor preparation, anticipation, restraint, execution and learning [4, 5]. So, we assumed that widely interactions in model of motor control were employed for future movement in human brain, and we also assumed that there was a similar circuit in human brain during left hand’s movement readiness state.

Using functional correlations analysis method, Newton et al. revealed significantly increased correlations within the sensorimotor networks (SMN) [1]. Fox and Raichles et al. found that default model network (DMN) and SMN were completely separated in resting state but anti-correlated in movement execution [6, 7]. Furthermore, Treserras et al. found that PCC were aroused prominent functional coupling with UPCU, right supplementary motor area (RSMA) and right primary sensorimotor cortex (RS1M1); however ACC delivered the prominent functional coupling to LS1M1 in right hand’s movementreadiness state [3]. These results just revealed the functional coupling in model of motor control in human brain; however, the directional causal flow in model of motor control is still lack.

Recently, there was a growing concern for interactions in model of motor control from the causal point of view. Using structural equation modeling (SEM), Solodkin et al. found that the input from supplementary motor area (SMA) to primary sensorimotor area (S1M1) was facilitated during movement execution (ME) [8]. Using dynamic causal modeling (DCM), Grefkes et al revealed enhanced neural coupling towards the contra lateral S1M1 but reduced towords ipsilateral S1M1 during unimanual ME [2]. There were some limitations in SEM and DCM methods, such as the requirement of prior directional connectivity information and low effects for multi-nodes situation. However, Granger causality (GC) method can effectively overcome these shortcomings. [9, 10]. Using GC method, Uddin et al found that PCC exerted greater influences on its anticorrelated networks [9]. Using GC method, Chen et al. found the forward and backward causal influences among SMA, the bilateral dorsal premotor area (PMd), the contra lateral primary and secondary somatosensory cortex (S1) and the primary motor cortex (M1) during motor imagery (MI) [10]. The GC method was just suitable for bi-variation situation. So, conditional Granger causality (CGC) method, which was an extend GC method, was proposed for multi-variation situation [7, 11-13]. Using CGC method, Liao et al found that self-referential network (SRN) exerted the strongest causal influences to other networks; however DMN was affected by other networks [14, 15]. These studies explored causal influences in model of motor control in ME or MI; however, the estimation of causal influences was still lack during movement-readiness state, and the existence of the whole dynamic circuit wasn’t validated in human brain during left hand’s movement readiness.

In the present study, CGC method was employed to resolve the aforementioned problems. Firstly, ACC, PCC, UPCU, left caudate nucleus (LCN), right caudate nucleus (RCN), CMA, LSMA, LS1M1, RSMA and RS1M1 were acquired by independent components analysis (ICA). CGC method was then employed to analyze the directed influence among these regions. Subsequently, the net CGC flows were acquired by subtracting bi-directional CGC values. Finally, the nonparametric bootstrap methodology was applied to assess the statistically significant threshold.

• II.    Material and methods

• A.    Subjects

Sixteen healthy subjects (8 female and 8 male, mean ages 24.8) without history of neurological and psychiatric disorder participated in the fMRI experiment. All participants were confirmed as right-handed using the Edinburgh Handedness Inventory and had normal or corrected-to-normal vision. Written informed consent was given prior to scanning. The experiments were approved by the local ethics committee.

• B.    Scanning procedures and tasks

  The experiment was performed on SIEMENS Trio 3T scanner, in Huaxi MR Research Center, Chengdu, China. The gradient-recalled echo planar imaging (EPI) sequence was employed for fMRI scanning and the parameters were as follows: 30 transverse slices, TR = 2000ms, TE = 30ms, FOV = 24cm, matrix = 64 X 64, voxel size = 3.75 X 3.75 X 5mm (without gap), flip angle = 90 ° . Subjects were required to remain still and relax with keeping their eyes closed until heard an oral signal ("ready"); then waiting for an oral signal ("move") before executing task (left hand grasping with ratio of 2 Hz); and finally, subjects were required to execute the sensorimotor task until heard the oral signal ("stop"). The whole tasks would also last 6 min 40 sec.

C. Data preprocessing and choosing region of interest(ROI)

The realignment was employed to reduce the effect of head motion. All realigned images were spatially normalized to the EPI template using registration. Spatial smoothing was employed to enhance the signal-to-noise ratio using a 6mm cubic Gaussian kernel with a full width half-maximum (FWHM). All these operations were completed in SPM8 (. The group ICA of the smoothed datasets of movementreadiness of all subjects was carried out in GIFT (Group ICA of fMRI Toolbox) [16]. Based on previous published results, 10 components were chosen, which were corresponded respectively to LSMA, RSMA, CMA, LS1M1, RS1M1 PCC, UPCU, ACC, LCN and RCN [3, 5].

D. CGC method

Based on the mathematic description of the CGC, a measure of linear dependence was proposed, which could effectively calculate GC in light of vector autoregressive models [7, 17, 18]. Consider three time series Xt ,Yt and Zt. Firstly, the joint autoregressive representation for Xt and Zt can be written as follow:

pp

X. = E a 1 j X t - j + E b j Z t - j + £ 1 j = 1                j = 1                                  (1)

pp

Z . = E ^c 1 j X t - j + E ^d 1 j Z t - j + ^£ 2. j = 1                 j = 1

where the covariance matrix of the residual noise terms is:

₄ cOv ( ^£ _{2 1} , £ ₁ )

c^oV ( ^£ 1 1 , ^£ 2 1 ) var ( ^£ 2 1 )

Then we consider the joint autoregressive representation of all three time courses Xt, Yt and Zt:

ppp

X1 = E a2 jXt-j + E b2 jY-j + E c2 jZt-j + £31 j=1                 j=1

ppp

Y =y d.X, ,+y e2Y ,+y fZ ,+ £ t           2 j 1 - j          2 j 1 - j         2 L j t - j4

j=1                 j=1

ppp t ° 2 j t - j           2 j t - j           2 j t - j 51

j = 1                  j = 1                j = 1

where the covariance matrix of the residual noise terms is:

E 2 =

" ^var ( ^£ 3 t ) COv ( ^£ 4 t , ^£ 3 t )

_v ^cov ( ^£ 5 , , ^£ 3 , )

COV ( £31, £41 ) COV ( £31, £51 Г var (£41)     cov (£41, £51 )

COV ( £51, £41 )     ^ ( £51 ) ,

where p is the order of the autoregressive model; and _£ i_t , i = 1,2,3,4,5 are the uncorrelated prediction error over time. From these two sets of equations, we define the conditional Granger causality from time-course Yt to Xt conditional on time-course Zt as:

F

Y ^ X | Z

= ln

var

var

(£11)) ( £31 )J

When the causal influence from time-course Yt to Xt is

entirely due to other time course Zt , the coefficients b2 j in Eq.3 are uniformly zero, and var ( £ 1 ₁ ) = var ( £ _{3 1} ) . So, F Y ^ XZ = 0 meaning that no further improvement in the

predication of time-course Xt can be expected by including past measurements of time-course Yt conditioned on the other time-course Zt. In contrast, when a direct influence from time-course Yt to Xt exists, the inclusion of past measurements of time-course Yt in addition to that of time-course Xt and Zt should result in better predictions of time-course Xt, leading tovar ( ^ 1 ) > var ( ^ 1 ) , and F _Y ^ X_XZ >  0^[12]

The order of the autoregressive model was set to 6 using the Schwarz criterion (SC). The coefficients of the models were calculated using a standard least squares optimization.

TABLE I.

T he detail information of ten ROI s

Node’s name	Brodmann area	Coordinate
ACC	10,24,32	-2,55,1
CMA	6,24,32	1,15,39
LCN	/	-12,15,6
LS1M1	2,3,4	-38,-19,65
LSMA	6	-10,2,60
PCC	23,30	-1,-50,20
UPCU	7	-1,-67,58
RCN	/	12,13,10
RS1M1	2,3,4	35,-34,68
RSMA	6	4,10,49

• E. Calculating net Causal flows among ROIs

The time course of each ROI was generated by averaging time courses of all voxels in ROI. Linear drift and linear regression were employed to eliminate the gross signal drifts, gross physiological changes, the artifacts of head moving, the interference from the signal of cerebrospinal fluid (CSF), white matter and individual response component, aiming to the state of movementexecution. CGC were employed to calculate the net causal flows among chosen ROIs during movement readiness state, using our programs coded in MATLAB (The Mathworks, Natick, MA) in terms of previous studies [17, 18]. The net direct flows as follow:

^FNET\Z = F Y ^ X | Z - ^FX ^ Y | Z ⁽⁶⁾

To assess the statistical significance of CGC results, a nonparametric estimation based on the bootstrap methodology was applied to obtain the null distribution [19].

• III.    Results

• A.    Choosing ten nodes

The Fig.1 revealed the spatial distribution for ten ROIs with a statistic threshold. The Table.1 enumerated the Brodmann area and the Talairach coordinates of peak voxels of ten nodes chosen by group ICA.

• B.    Net causal flows in left hand’s movement-readiness state

The Fig.2 revealed the map for CGC in left hand’s movement-readiness state. The Table.2 enumerated the detail of the mean of CGC across sixteen subjects. Each row meant F x ^ y\z and each column meant F y ^ x\z . Some nodes (especially CMA and UPCU) revealed lateralization of interaction in left hand’s movementreadiness state. CMA revealed net causal influences with RCN and RSMA, UPCU exerted net causal directional influence to RCN at the same time.

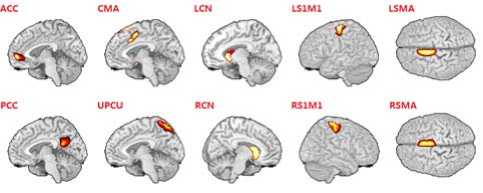
Figure 1. The location map of ten ROIs.

TABLE II.

T he values of CGC during left hand ’ s movement - readiness

	1	2	3	4	5	6	7	8	9	10
1	/	/	/	/	/	.007	/	/	/	/
2	/	/	/	/	/	/	/	/	/	.008
3	/	/	/	/	/	.005	/	/	/	/
4	/	/	/	/	/	/	/	/	/	/
5	/	/	/	/	/	/	/	/	/	/
6	/	/	/	.004	/	/	.01	/	/	/
7	/	/	/	/	/	/	/	.007	/	/
8	/	.007	/	/	/	/	/	/	/	/
9	.004	/	/	.006	/	.006	/	.01	/	/
10	/	/	/	.004	/	/	/	/	.004	/

1=ACC, 2= CMA, 3=LCN, 4=LS1M1, 5=LSMA, 6=PCC, 7=UPCU, 8=RCN, 9=RS1M1, 10=RSMA

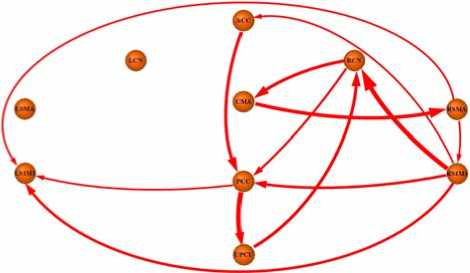
Figure 2. The map of net causal influences in left hand’s movementreadiness state

• C.    Out-In degrees of ten nodes in left hand’s movement readiness state

The Fig.3 revealed the map of Out-In degrees of ten nodes in left hand’s movement-readiness state. In the Fig.3, RS1M1 revealed highest positive Out-In degrees, however, LS1M1 revealed highest negative Out-In degree

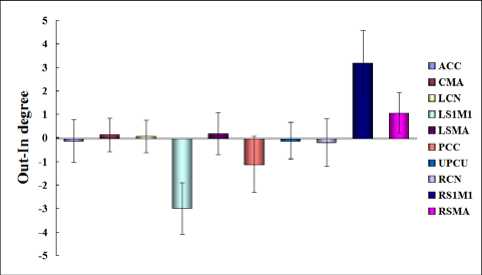
Figure 3. The map of net causal influences in left hand’s movementreadiness state

• D.    A circuit in left hand’s movement readiness state

The Fig.4 revealed a circuit during left hand’s movement readiness state, which was consisted with the circuit in monkey’s brain and was similar but mirrorimage as that found during right hand’s movement readiness state. The circuit passed through seven nodes as follow:

ACC → PCC → UPCU → CN → CMA → SMA → S 1 M 1 → ACC

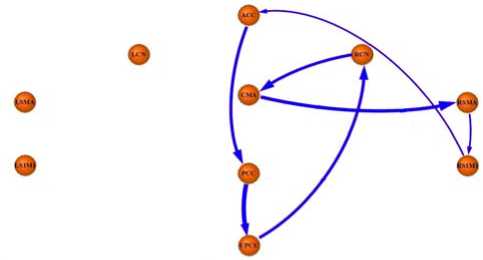
Figure 4. The map of a circuit during left hand’s movement readiness state

• IV.    Discussion

In the present study, the CGC method was applied successfully to investigate the interactions among ten nodes involving motor control in left hand’s movementreadiness state. Our result showed that CMA revealed net causal influences with nodes in right SMN and in right corpus striatum, UPCU revealed net causal influence with node in right corpus striatum. Based on net causal flows among nodes, we found a circuit which was similar but enantiomorphous to that found in right hand’s movement readiness state. Moreover, the results of Out-In degrees indicated that RS1M1 preferred modulating other nodes, in contrast, LS1M1 preferred being affected by other nodes in circuit of motor control during left hand’s movement-readiness state.

• A.    Net causal influences during left hand’s movement readiness state

  The net uni-directional influence from UPCU to RCN was consisted with the previous research in monkey corticocortical connections [3, 5, 20, 21]. The limbic system upstream was anatomically connected by UPCU with the sensorimotor system downstream which involved in hand motor representation [5, 22]. Moreover, UPCU was also related to mental motor imagery, spatial control of hand movement, generating successively underway movement in terms of buffered memory [2326]. Treserras et al assumed that the UPCU devoted to multimodal sensory integration [3]. CN was an authorization structure for motor control which received the information of premotor processed sent by limbic system, and then processed the information at highest cognitive level [4, 27-29]. So, in the present study, net causal influence from UPCU to RCN indicated that RCN collected initiatory messages sending by UPCU during left hand’s movement-readiness [4, 30]. The net unidirectional influence from RCN to CMA and that from CMA to RSMA were consisted with the previous research in monkey corticocortical connections [3, 5, 20, 21]. In fact, CMA was a key region associating with response and choice of optimal planning and task control function [4, 27, 30, 31-33]. The potential mechanism was that CMA received numerous optimal plans for movement from RCN; then generating a reasonable response selection for left hand’s movement; and finally sent a facilitated signal to RSMA during left hand’s movement-readiness [4, 20, 21].

• B.    A circuit in left hand’s movement readiness state

Firstly, our results revealed that net causal flows could construct a circuit as follow:

ACC → PCC → UPCU → RCN → CMA → RSMA → RS1M1 → ACC . The circuit was similar to that found in monkey cortico-cortical connections and was also similar but mirrorimage as that found in right hand’s movement readiness [3, 5]. So, the circuit confirmed our hypothesis in previous research from view of dynamic causality. The ACC as part of the rostral limbic system was a key region generating behavior predictions and guiding our actions, playing emotive and motivational role in motor behavior [20, 21, 34-36]. Hence, ACC transmitting net causal flow to PCC suggested that ACC generated initialized information flowing to the PCC [37-40]. PCC was a centre which play important role in reviewing past knowledge [5, 41]. The potential mechanism for the net causal flow from PCC to UPCU might be that PCC reviewed fix behavior pattern and sent an initialization to UPCU for movement readiness. The UPCU was an intermedia region which connects anatomically with the limbic system upstream and with the sensorimotor system downstream treating of hand motor representation [5, 22]. Moreover, UPCU involved in mental MI, spatial control of hand movement, generating successively underway movement in terms of buffered memory [23-26]. Treserras et al. thereby suggested that UPCU devoted to multimodal sensory integration and found UPCU aroused functional connectivity with PCC [3]. In the present study, the net causal flow from UPCU to RCN suggested that RCN collected initiatory messages sent by UPCU [5, 30]. The caudate nucleus (CN) was an authorization structure for motor control which received the information of premotor processed by limbic system and then processed the information at highest cognitive level [5, 27-29]. The net causal flow from RCN to CMA suggested information communication for response and choice of optimal planning [5, 27, 30]. CMA was a key region associated with task control function [31-33]. The potential mechanism of net causal flow from CMA to RSMA was that CMA received numerous optimal plans for movement from RCN, then generating a reasonable response selection for left hand’s movement, and finally sent a facilitated signal to RSMA [5, 21]. Due to the SMA was related to motor output, the net causal flow from RSMA to RS1M1 was regarded as the facilitation during left hand’s movement readiness [2, 42, 43]. Finally, the net causal flow from RS1M1 to ACC implied that the initial information sent by ACC was returned to ACC by passing through upmentioned closed circuit in the present study. This feedback might suggest a reinforced process for the currency of information flow in the circuit. In general, this circuit was consisted with most parts of circuit in monkey study and was similar but mirrorimage as that found in human brain during right hand’s movement readiness. This result suggested that there was an intrinsic circuit for motor control during either right hand’s or left hand’s movement readiness. The intrinsic circuit can be described as follow:

ACC → PCC → UPCU → CN → CMA → SMA → S 1 M 1 → ACC .

In addition, there were other causal flows which could be regarded as an inhibitory role for task demand in the present study. The net causal flow from RSMA to LS1M1, which was consisted with the previous results, might imply an inhibitory process from RSMA to LS1M1 during left hand’s movement readiness [2]. At the same time, the previous functional connectivity research indicated that coupling between RS1M1 and LS1M1 decreased, whereas coupling between RS1M1 and RSMA increased during left hand’s movement-readiness state [1, 3]. Our net causal flow revealed that RS1M1 received net causal flow from RSMA and transmitted net causal flow to LS1M1, suggesting potential modulations of coupling between RS1M1 and RSMA during left hand’s movement readiness [10, 44-47]. The previous results suggested that PCC aroused enhanced functional connectivity with RS1M1, implying some interactions among two nodes in right hand’s movement readiness state [3, 48]. Our results showed that PCC received significant net causal flow from RS1M1 and transmitted significant net causal flow to LS1M1 in left hand’s movement readiness state, providing an indirectly evidence for the upmentioned suggestion. In addition, these results also indicated that PCC as a relay station transmitted the inhibitory information from one side of SMN to another side during unimanual behaviors. This suggestion might imply the potential mechanism that PCC mediated the coupling between SMN in two hemispheres for task demand. In general, based on net causal flows among nodes, we found a circuit which was similar but mirrorimage as that found in right hand’s movement readiness state. The result suggested that there was an intrinsic circuit for motor control during either right hand’s or left hand’s movement readiness. In additional, our findings revealed more interactions among nodes in human brain than in monkey brain. The potential mechanism might attribute to more complex cognitive processing and more modulation among nodes in the circuit for robusticity of the circuit [3, 9, 26, 35, 36, 49, 50].

• C.    Out-In degrees of ten nodes in left hand’s movementreadiness state

In the Fig.3, highest negative Out-In degrees indicated that LS1M1 preferred being affected by other nodes in circuit of motor control during left hand’s movementreadiness. In the present study, LS1M1 was exerted net uni-directional influence by RS1M1, RSMA and PCC. The net influences from RSMA and from RS1M1 to LS1M1 were consisted with the previous results, implying inhibitory modulations from right SMN to LS1M1 during left hand’s movement-readiness [2]. The net influence from PCC to LS1M1, which was consisted with the inference of the previous study on functional connectivity between PCC and RS1M1, suggested that PCC mediated the coupling between SMN in two hemispheres for task demand in the present study [3]. In the Fig.3, highest positive Out-In degrees indicated that RS1M1 preferred modulating other nodes in circuit of motor control during left hand’s movement-readiness. In the present study, RS1M1 exerted net uni-directional influences to LS1M1, ACC, RCN and PCC. The net influence from RS1M1 to PCC suggested that RS1M1 suppressed PCC for task demand in the present study [3]. The previous research revealed that RCN functionally coupled with RS1M1 during the resting state [51]. In the present study, the net influence from RS1M1 to RCN could be regarded as a part of a closed local circuit as follow RCN → CMA → RSMA → RS 1 M 1 → RCN . This result might suggest that RS1M1 exerted facilitated modulation to RCN for the currency of the circuit during left hand’s movement-readiness.

• V.    Conclusion

In the present study, fMRI and CGC were adopted successfully to investigate the interactions among ten nodes involving motor control in left hand’s movement readiness state. Our result revealed that a net causal flow passed through UPCU, RCN, CMA and RSMA in turn during left hand’s movement-readiness. Based on net causal flows among nodes, we found a circuit which was similar but enantiomorphous to that found in right hand’s movement readiness state. The result suggested that there was an intrinsic circuit for motor control during either right hand’s or left hand’s movement readiness. Moreover, the results of Out-In degrees indicated that bilateral primary sensorimotor areas revealed competitive relationship during unimanual movement-readiness.

Acknowledgment

This work is supported by the Natural Science Foundation of China (61035006 , 30900326 and 90820006 ). And supported by Program for Chang jiang Scholars and Innovative Research Team in University