Analysis of spacecraft orbital motion stability of Gonets-M No 37152

Introduction. The flatness of the Earth leads to the displacement of the satellite orbit perigee [1]. However, after consideration of the orbit group parameters of Gn-M, it was observed that the orbit apsidal line of SC No 37152 vice versa practically retains its position. Despite the fact that the orbital plane inclination of Gn-M is different from the critical value (the critical inclination equal to 63.43 degrees and 116.57 degrees).

It was found out that after the reduction correction Gn-M No 37152 hit the target orbit at a height of 1500 km with an inclination of 82.5 degrees with special laws changes in the orbit parameters – frozen orbit.

The study of the evolution of the orbital parameters e and w of Gn-M. A frozen orbit is an orbit whose mid elements, particularly the eccentricity e and the perigee argument w , for a long period of time can take almost constant or within a limited range enclosed values [2–4].

Analysis was studied by measurements of current navigation parameters (MCNP) of SC’s No 37152, No 38736, No 38734 which are located in the same orbital plane. Special attention was paid to the following SC orbit parameters: e , w and the nodical period T nd .

Due to the analysis it turned out that the parameters, obtained after processing MCNP of SC’s No 38736, No 38734 behave in the following way: w changes in the range from 0 degree to 360 degrees, i. e., it has secular changes, e changes in the range from 0.001 to 0.003. The nodical period Tnd in addition to the secular component has got a long-period one. On the other hand, orbit parameters w and e of SC No 37152 change in a completely different way (tab. 1).

It must be noted that SC No 37152 is different in behavior of the considering orbital motion elements according to its own points A1–A5 (tab. 1) in comparison with parameter values at points B1–B5 and C1–C5 of other SC’s and in addition to this its secular component of the perigee argument change disappeared.

Therefore, further for the study, we take the values obtained by MCNP, orbit parameters e and w of SC’s No 37152, No 37836 and No 38734 over a period of one year (tab. 1) and compare these values with the predicted values of e and w . The forecast will be carried out taking into account the influence of the Sun, moon and the resistance of the atmosphere over a period of one year. All the corresponding values will be presented in one graph (fig. 1–3).

Table 1

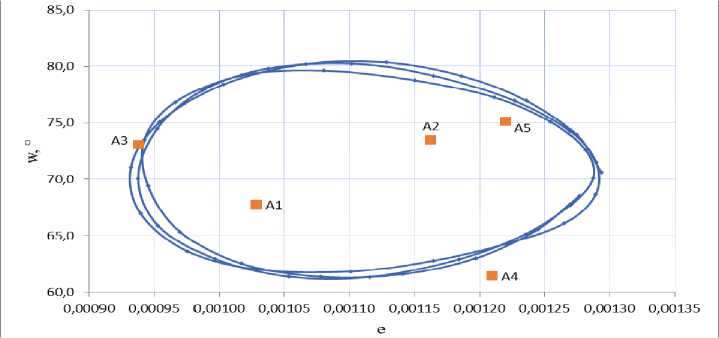
Fig. 1. e , w orbit parameters change of SC No 37152 over a period of one year

The MCNP results of SC’s No 37152, No 38736, No 38734

SC No 37152

№	Date	Т nd , с	e	w , °	i , °
А1	04.06.16	6955.066	0.0010284	67.778	82.460
А2	06.07.16	6955.067	0.0011624	73.497	82.460
А3	06.11.16	6955.046	0.0009379	73.050	82.459
А4	06.03.17	6955.042	0.0012092	61.417	82.461
А5	07.07.17	6955.019	0.0012199	75.115	82.463
SC No 38736
№	Date	Т nd , с	e	w , °	i , °
B1	29.06.16	6955.032	0.0032782	70.250	82.484
B2	22.09.16	6954.957	0.0010319	238.830	82.484
B3	16.11.16	6954.955	0.0028615	107.508	82.487
B4	17.03.17	6954.950	0.0011888	197.741	82.488
B5	17.07.17	6954.914	0.0019047	349.824	82.486
SC No 38734
№	Date	Т nd , с	e	w , °	i , °
С1	29.06.16	6954.913	0.0030670	69.888	82.479
С2	21.08.16	6954.883	0.0017654	177.554	82.475
С3	26.11.16	6954.899	0.0028563	91.390	82.482
С4	27.03.17	6954.905	0.0014133	163.996	82.484
С5	05.05.17	6954.892	0.0027339	99.380	82.483

Рис. 1. Изменение параметров е , w на орбите КА № 37152 на интервале одного года

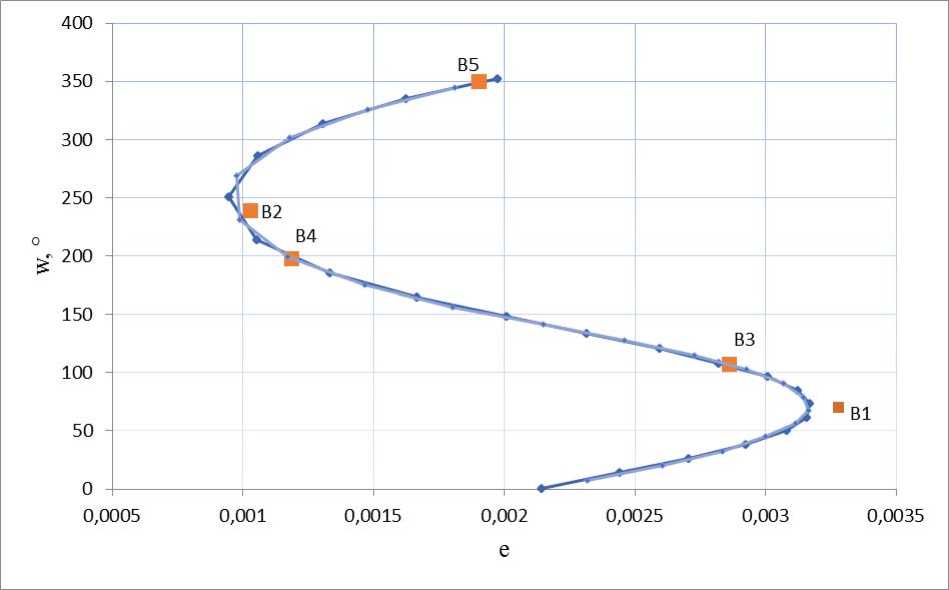
Fig. 2. e , w orbit parameters change of SC No 38736 over a period of one year

Рис. 2. Изменение параметров е , w на орбите КА № 38736 на интервале одного года

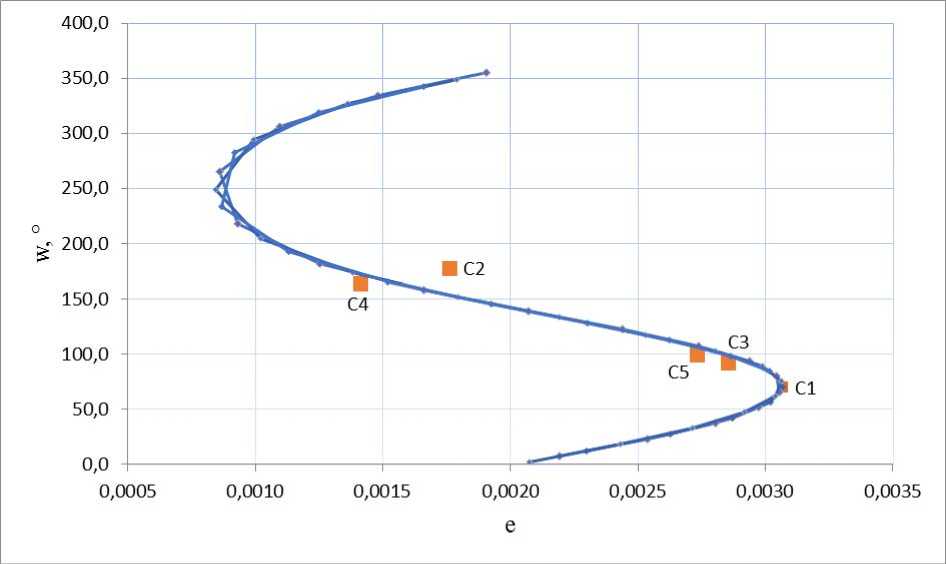
Fig. 3. e , w orbit parameters change of SC No 38734 over a period of one year

Рис. 3. Изменение параметров е , w на орбите КА № 38734 на интервале одного года

At the fig. 1, 2 and 3 it can be seen that the values obtained by MCNP are in good agreement with the values calculated by the forecast of SC orbit motion.

Looking at tab. 1 and fig. 1 it can be concluded that in a frozen orbit parameters e and w of SC No 37152 are changing in the following intervals of values

0.0009 <  e < 0.0013; 60.0° <  w < 80.0° (1)

The obtained inequalities of e and w changes are assumed as a condition for SC being in a frozen orbit at an orbit height of 1500 km with an inclination of 82.5 degrees.

The orbit period changes of Gn-M. Consideration should be given to the nodical period T nd of Gn-M. The observation of the T nd secular changes according to the NORAD database [5] shows that SC No 37152 has significant decreasing of the amplitude of the long-period component in the nodical period, compared to SC No 38736 and SC No 38734 of the same orbital plane and of the same location in a non-frozen orbit (fig. 4).

It is necessary to pay attention to one more feature of carrying out calculations by T nd using. It is talked about the influence of TGF tesserial harmonics on the average anomaly. These harmonics cause secular perturbation in the average anomaly, what corresponds to the SC secular drift along the trajectory. This secular drift should be taken into account in project calculations where the initial conditions are the use of the sculating orbital elements at some point. If T nd is used as initial conditions, this perturbation should not be taken into account, since it is included as a component of nodical period initial value [6; 7].

The analysis of the secular change in T nd circulation period by all three SCs Gn-M shows that every SC T nd value over a period of one year, starting since 01.06.2016, decreased an average of ~ 0.04 s.

Considering fig. 4 in greater detail, the significant amplitude decreasing of the long-period component can be noted in the nodical period of Gn-M No 37152. The changing nature of treatment period became smooth over time.

The difference in T nd values changes of SC No 37152 and T nd of other orbit group SCs can be explained due to the influence of long-period perturbations [8].

The oscillation amplitude changes of Gn-M sidereal period in orbit. The long-period component is generated by the long-period oscillations of the nodical period, which have an amplitude [9–11]

А т = 3- C 2^ (R _э/ a ) 2 T nd (2 - (5-sin 2 ( i ))/2)- e , (2)

where C _2.0 = –1082.627∙10^–6 – dimensionless constant characterizing the shape of the Earth; R _э = 6378.16 km -the equatorial radius of the Earth [12; 13]; e – the eccentricity of orbit turn; a = 7878.16 km – a large orbit axis; T nd = 6955.0 s – the initial value of Gn-M orbit nodical period [14]; i = 82.5 degrees – the inclination of orbital plane.

On substituting values into expression (2), the following formula is obtained

А Т = 6.8∙ e . (3)

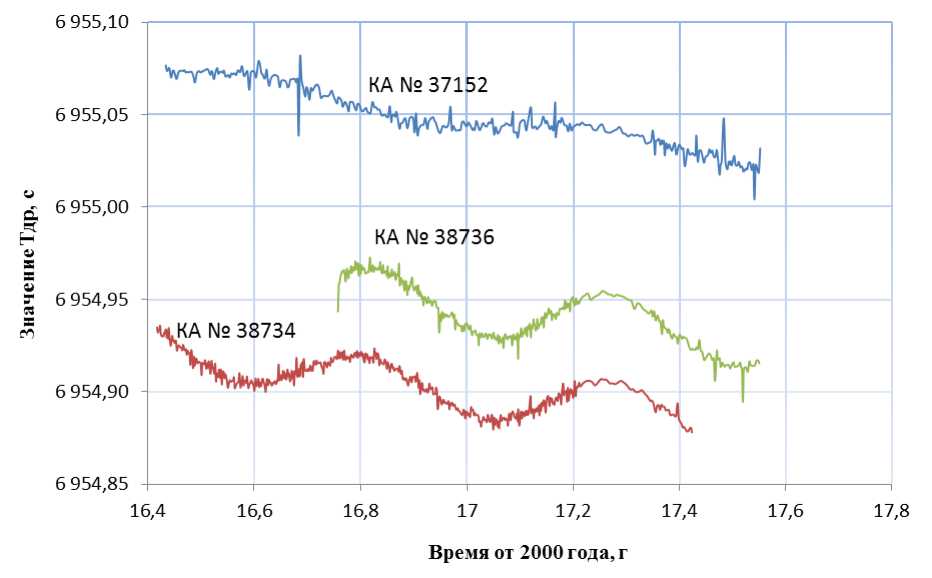
Fig. 4. T nd change of SC No 37152, SC No 38736 and SC No 38734

Рис. 4. Изменение Т _др КА № 37152, КА № 38736 и КА № 38734

Table 2

A T , ( T nd ) dk calculations results following MCNP data

SC No 37152
Date	e	w , °	А Т	( Т nd) dk , с	1/2∙( Т nd ) dk , с
04.06.16	0.0010284	67.778	0.00699	–0.00265	–0.00133
06.07.16	0.0011624	73.497	0.00790	–0.00225	–0.00113
06.11.16	0.0009379	73.050	0.00638	–0.00186	–0.00093
06.03.17	0.0012092	61.417	0.00822	–0.00394	–0.00197
07.07.17	0.0012199	75.115	0.00830	–0.00214	–0.00107
SC No 38736
Date	e	w , °	АТ	( Т nd) dk , с	1/2∙( Т nd) dk , с
29.06.16	0.0032782	70.250	0.02229	–0.00755	–0.00377
22.09.16	0.0010319	238.830	0.00702	0.00364	0.00182
16.11.16	0.0028615	107.508	0.01946	0.00584	0.00292
17.03.17	0.0011888	197.741	0.00808	0.00770	0.00385
17.07.17	0.0019047	349.824	0.01295	–0.01274	–0.00637
SC No 38734
Date	e	w , °	АТ	( Т nd) dk , с	1/2∙( Т nd) dk , с
29.06.16	0.0030670	69.888	0.02086	–0.00718	–0.00359
21.08.16	0.0017654	177.554	0.01200	0.01199	0.00600
26.11.16	0.0028563	91.390	0.01942	0.00046	0.00023
27.03.17	0.0014133	163.996	0.00961	0.00923	0.00462
05.05.17	0.0027339	99.380	0.01859	0.00301	0.00151

In this case, the long-period oscillations of nodical period ( T nd ) dk at the time of equator passing take the following form [9–11] in the turn

( Т nd ) _dk = – А_Т ∙cos( w ), (4) where w is the value of the orbit perigee argument in the turn.

Following MCNP data the Gn-M orbits eccentricity is being ranged between 0.001 and 0.004. It follows that the long-period component amplitude of the nodical period А_Т is 0.007–0.030 s according to the formula (3).

If Gn-M No 37152 is moving along frozen orbit, its А_Т change is different. To check this situation actual values obtained by MCNP, w and e parametres results are taken out of the tab. 1, formulas (3), (4) are used for calculations (tab. 2). In tab. 2 parameter 1/2 ∙ ( T nd ) dk means the semirange of T nd long-period oscillations.

It must be noted that the value (T nd ) dk depends on time. Comparing presented in tab. 2 parameter 1/2∙(T nd ) dk with the values of the T nd . behavior by its real observations (see fig. 4) it can be seen that in both cases the semirange of the long-period oscillations of T_nd period is about 0.001 s in magnitude. In the tab. 2 t SC No 37152 eccentricity changes from 0.0009 to 0.0013, thus the long-period component amplitude of the nodical period changes in closer limits from 0.007 to 0.009 s.

Conclusion. Presented data point to a potentially promising application area of orbits as a frozen orbit. The detection of the nature changes in the motion of SC Gn-M No 37152 in such an orbit can aid in improving the calculation accuracy of orbit correction parameters, which will be relevant by increasing the number of Gn-M orbit groups, as is proposed in [15], and by a significant reduction of SC retention area at the necessary points of standing, i. e., in connection with the requirements increasing to the structural stability of the orbital group.