Analysis of the Time Trends of Precipitation over Mediterranean Region

Published Online August 2014 in MECS

Precipitation, as a major parameter in the hydrological cycle, is of great importance for all aspects of human life. In general, precipitation can be decomposed into two types; convective and stratiform  [1,2].  Convective precipitation is characterized by a large vertical extent and is more intense and of shorter duration than the stratiform precipitation. Stratiform precipitation, however, usually covers large areas horizontally, and it often forms in areas adjacent to convective cells, which contribute to a significant portion (40-50%) of rainfall, even for intense convective systems.

The Mediterranean region has a complex orography and land-sea contrast very marked. Due to these geographical properties, the climate has unstable spatial and temporal characteristics. This climate is influenced both by the tropical climate and the climate of midlatitude systems. Mediterranean rainfall is extremely variable in this region. Storms occurring in the Mediterranean region provide high intensity and are usually associated with convective events. In Algeria in recent years, there has been a marked decrease in rainfall, with very serious consequences especially in areas where the rainfall amount and distribution were already barely adequate. From an agronomic perspective, the persistent drought during the rainy season is crucial for starting agricultural activities.

In this context, analysis of precipitation data is of great interest to interpret and to predict behavior rainfall as well as to assist in planning and management of water resources. Furthermore, a good description of the stochastic rainfall can help especially in the detection and evaluation of risk situations.

Several statistical techniques to analyze rainfall data collected by rain gauges networks have been published in the literature [3-6]. The models used for this purpose can be grouped into four categories, conditional models, random cascade models, Markov chain models and nonparametric models [7,8]. The first two models require large amounts of data and thereby calculations are intensive [9]. In contrast, parametric models, when their conditions are satisfied, they are more powerful than nonparametric models [9,10].

Therefore, the model, which is widely used to study random phenomena, is the model based on Markov chains. The traditional notion of randomness has been studied by Koutsoyiannis [11]. It has been often used for analyzing of precipitation [12, 13, 3, 14,]. The first users of Markov chains have shown that it is adequate to describe the sequences of dry days and wet days [15, 16]. The advantage of Markov chains has been highlighted by some authors [15, 17, 18]. Jimoh and Webster [19] showed that the order one of a Markov model is sufficient to represent the chronological behavior of precipitation.

For this reason, we chose to use Markov chains due to its robustness and because it directly takes into account the influence of the recent past on the next immediate. This chain is a stochastic model, iterative, which determines the probability of transition from a state to another, or a persistent state of a system.

However, many techniques have used only two states (wet, dry) to characterize the precipitation. The scale considered in the best case, was daily [20, 21]. Indeed, no analysis took into account the variability of rainfall intensity and also no analysis have been carried out at the time scale of the radar observation. Methods are used to predict rainfall using Artificial Neural Network [22].

Precipitation is characterized by a high variability in space, time and intensity. Historically, precipitation has been observed locally by rain gauges, often only as accumulated daily amounts. The global distribution of gauges is quite variable, from relatively dense networks in the developed countries to sparsely distributed gauges in developing regions. Over oceans, gauges are almost non-existent, with only a few of them on Algeria. Furthermore, the rain gauge networks provide measurements of precipitation only where they are installed. In Algeria, these data are measured at the time scale “daily”, which is not sufficient for a study on an appropriate scale. However, radar data are available in real time, and collected even in remote areas where data are difficult or impossible to collect by rain gauges networks. The radar provides continuous coverage in time and space of precipitation fields. The coastal radar offers the particular advantage of being a tool to study the behavior of precipitation both on sea and on ground. Its measurements are widely used for hydrological purposes and in the prevention of natural disasters.

For this purpose, our contribution in this paper is to provide a better description of precipitation chronological behavior over the sea and the ground, using measurements of instantaneous weather radar. It is applied to the complex situation of the Mediterranean climate of this region. The probabilistic approach used here is a Markov chain of first order with three states.

• II.    Presentation Of Study Region And Data

Algeria is located on the south shore of the Mediterranean and is bordered to the east by Tunisia and Libya to the south by Niger and Mali, southwest by Mauritania and Western Sahara and the west by Morocco. The rainfall spatial distribution is characterized by a north-south gradient very marked and east-west gradient very low. The rainy season extends from October to March, with maximum rainfall occurring during November-December. In the north, the climate is Mediterranean transit, marked by seasonal oscillations. The annual rainfall average is estimated at about 600 mm. The minimum rainfall is recorded in the southern regions, it is about 50 mm, while the maximum is observed in the Djurdjura massif located in Kabylia and the massif of Edough located at east, where it exceeds 1 500 mm.

The radar data used in this study are collected by the radar of Setif (Algeria). This coastal radar located at latitude 36 ° N, longitude 05 ° E with an altitude of 1033m, it records an image of size 512 x 512 pixels every fifteen minutes. Each pixel coded on four bits, it has a resolution of one km². The representative physical parameter of the radar reflectivity factor is noted Z (mm⁶m^_3) . The conversion of reflectivity factor Z into rainfall intensity R(mm/h) is obtained using (1) adapted to our Radar.

Z = 300 * R 1.5. (1)

The Z can also be converted into dBZ .

The displacement in azimuth is between 0 to 360 degrees in continuous and the movement in inclination is between -20 ° to 90 °. Its polarization is linear and horizontal. The technical characteristics of used radar are: Wavelength (5.5cm), Peak power (250kw), Repetition frequency (250Hz) and Pulse duration (4µs).

The data consist of a series of 17660 images by season (October to March) collected by the meteorological radar of Setif (Algeria). The datasets are divided into a training and a validation data set. The training data set is used for the development of the technique and collected from October 2001 to March 2002. The validation data set is considered for the appraisal of the proposed technique is recorded during the rainy seasons, 2002/2003, 2003/2004, 2004/2005, 2005/2006 (Table 1).

• III.    Methodology

• A.    Selection of ground and sea area

Two study areas have been selected on the radar domain. One area is located over the sea and other over the ground (Fig. 1). We only set the size of the area to 15 x 15km2. This is to avoid high values of the variance of pixels in the area, which may skew the classification. This situation can occur when a part of precipitation systems pass over the area. The values of each area are obtained by using (2) which represents the weighted average on the 15x15 pixels of the area.

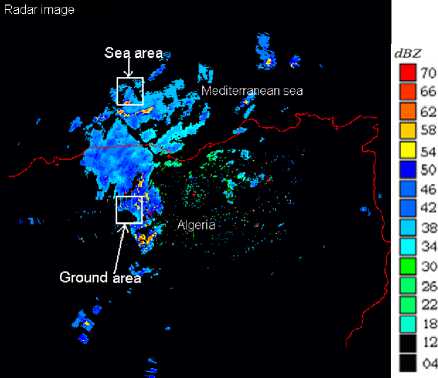
Fig. 1. Localisation of study areas (Ground area and Sea area) in Radar image

• B.    Rainfall type

In general, rainfall can be decomposed into two types; convective and stratiform. Convective precipitation is characterized by a large vertical extension and is more intense and of shorter duration than the stratiform precipitation. Stratiform precipitation, however, usually covers large areas horizontally, and it often forms in areas adjacent to convective cells.

The radar reflectivity maps can be used to diagnose stratiform and convective precipitation fields. Convective precipitation is characterized by high reflectivity and a clearer spatial intensity gradient. Several authors propose thresholds to identify convective clouds [21]. The National office of meteorology (O.N.M.) of Algiers had adopted the threshold 42 dBZ from which convective clouds are identified. The experiment conducted by the O.N.M. showed that on 422 events of a convective data sets references, 89% of these events are identified on the weather radar reflectivities using the threshold 42 dBZ. Below of this threshold, stratiform precipitation is detected. Therefore, in order to classify radar data, we considered that all convective precipitation (first class), lie in the interval (≥42 dBZ) and all stratiform precipitation (second class) have values between 18 dBZ and 42 dBZ (42 dBZ not included). The third class is the class no raining, it is obtained for all reflectivities less than 18 dBZ.

The weighted mean representing the reflectivities of 15x 15 pixels from one area, which will be compared with thresholds to determine its class, is calculated by applying (2):

MP =

S X1( C (i, j) *P (i, j)) Ш (i. j)

Where P(i,j) is the pixel value (in dBZ ) at position i and j of 15x15 pixels. C(i,j) is the weighting coefficient depending on the position i and j of a pixel.

The largest coefficient is the central pixel, the farther away from the center, the coefficient value decreases.

We plotted curves showing the evolution of the weighted average of reflectivity factors of 15 x 15 pixels for each of the two areas during the study period (Fig. 2). It should be noted that these data have been acquired with a time step of fifteen minutes (temporal resolution of the radar).

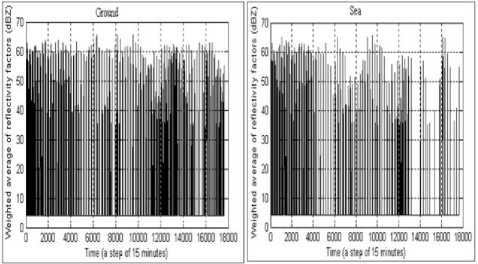
Fig. 2. The evolution of weighted mean of radar reflectivities over time

• C.    Time series of Rainfall

Precipitation is classified into three states, stratiform state or convective state, and a third to represent the no raining state. These states are obtained from the following decision criteria:

• •    Convective state ( S 2 : heavy rainfall): if MP>42dBZ

• •    Stratiform state ( S 1 : average rainfall): if 18 dBZ42dBZ

• •    No raining state ( S 0 : low or no rainfall): if MP< 18 dBZ

  The 17660 images that we have used in this study correspond to a period of six months, from October 2001 to March 2002. At each radar observation, a state, which is based on the weighting coefficient calculated by applying (2), is defined as, either high rainfall, average rainfall or no raining. Thereby, we obtain time series of precipitation, one observed over ground and other over sea. Each is composed of three states, namely "convective", "stratiform" and "no raining". The appearances states according the rainy season and study area are given in table 1.

Table 1. Tabulated summary data

Rainy season	Type of use	Study area	Appearances states
			Convective	Stratiform	No-raining
2001/02	Training	Ground Sea	2528 1504	6271 5195	8861 10961
2002/03	Validation	Ground Sea	2511 1425	6309 5200	8840 11035
2003/04	Validation	Ground Sea	2630 1524	6254 5240	8776 10896
2004/05	Validation	Ground Sea	2701 2200	6442 5896	8517 9564
2005/06	Validation	Ground Sea	2653 1987	6457 6003	8550 9670

• D.    Markov chain

A Markov chain can be described as a set of states, S={S 0 ,S 1 ,…,S m } , where the process begins in one of these states and transits from one state to another.

If the chain is in a state S i at time t , it switches to S j at time t+1 with a probability which is noted P ij . The probabilities P_i j are called transition probabilities. The process may persist in a state with a probability P ii . An initial probability distribution defines the state of the chain at time (t=0), which specifies the initial state.

With a sequence of states in discrete time, the transition probability of the variable of state S(t) at time t depends only on its state at time t-1 . The general form of these probabilities is given by the following expression:

Pij = Pr[S(t +1) = Sj / S(t) = Si ]. (3)

These probabilities can be grouped into a matrix, called the transition matrix and given by the following expression (4):

M =

p

p

0 m

.

p m0

P mm

They are calculated using (5):

The determination of transition probabilities is an important part for the forcast of precipitation behavior. For this case study, nine transition probabilities are determined from the Markov chain. These probabilities are grouped into the following matrix (8) :

N

P = -^ ij    N

.

	" P 00	P 01	p" 02
M =	P 10	P 11	P 12
	_ P 20	P 21	P 22 _

Where i and j=0,1,…,m. N ij is the number of transitions from state S i to state S j , and N i is the number of transitions from state S i to any other state.

For a Markov chain with finite state space and transition matrix M , the evolution over time of the initial probability distribution Q (0) is given by:

Q ( n ) = Q ( n - 1) * M = - = Q (0) * Mⁿ                (6)

Where Q(n) is the probability vector at time n . The probability vector is given by the following form:

Q ( t ) = [ P ( S o )   P ( S 1 )   -   P ( S m ) ]             (7)

Where P(S k ) is the probability of the state S k with k=0,1,…,or m.

• E.    Analysis using a Markov chain of first order with three states

To analyze the two time series of precipitation obtained in the previous sections by using Markov chains, we set the following assumptions:

• •    The precipitation process is described by state space

S={S 0 ,S 1 ,S 2 } , this is a Markov chain with finite state space.

• •    The evolution of phenomenon is random: it is a stochastic process.

• •    The future depends only on the present; it verifies the Markov property (no memory): this is a Markov chain.

• •    Possible developments of the process does not depend on time, the system verifies the homogeneity property: this is a homogeneous Markov chain.

We therefore used a Markov chain of first order with a state space S={S₀,S₁,S₂} . The time series of precipitation are modeled by the graph of the chain given in Fig. 3.

• IV. Results

  It should be noted that three states representing rainfall are considered in this study. The state of high precipitation corresponds to convective precipitation, the state of average precipitation corresponds to stratiform precipitation and the third state is no raining state. A transition matrix has been determined for each of the two study areas during the rainy season from October 2001 to March 2002. The elements of these matrices are calculated using (5). The results are given in Table 2.

Table 2. Results of Transition probabilities matrix

Study area	Ground			Sea
	S 0	S 1	S 2	S 0	S 1	S 2
S 0	0.83	0.14	0.03	0.88	0.11	0.01
S 1	0.25	0.61	0.14	0.22	0.67	0.11
S 2	0.07	0.41	0.52	0.06	0.37	0.57

The results show that the probability of finding the same state at the next moment is stronger than that to find a different state for the two areas. The probability of transiting from convective or no raining to no raining or convective, respectively is near zero. For the two areas, these probabilities are interpreted as follows:

• •    If we have a no raining state, the probability to have a stratiform state at the next moment is greater than the probability to have a convective state.

• •    The probability of a stratiform state pass to convection state is lower than the probability to transit to no raining state.

The probability that a convective state is followed by stratiform state is higher than the probability to be followed by no raining state.

• A.    Simulation

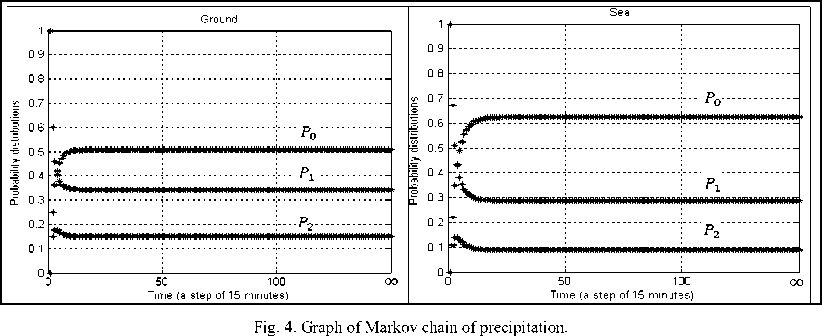
  According to the theory of Markov stochastic process, we use the transition probability matrix and the initial probability vector to predict the evolution of probability distribution over time, during the rainy season from October 2002 to March 2003. Using (6), we calculated the probability of each state at every moment during the prediction period. The curves showing the evolution of these probabilities are given in Fig. 4.

Results show that the evolution of probability distributions tends towards stationary probabilities. The probability of having a convective or stratiform state is low in sea and in ground. Note that for these two states, however, the probability is smaller in the sea area than in the ground area. In contrast, for the no raining case, the probability values are high for both areas, but more important in sea area than in ground area.

• B.    Validation

  To test our model, we have compared the stationary probabilities estimated previously by applying Markov chains with the actual probabilities of validation data. The validation data are collected during the rainy season from October to March of the period 2002/2003, 2003/2004, 2004/2005 and 2005/2006. These data are independent of all data used in the methodology. We calculated the actual probabilities using (9):

PA, = N i_N

.

Where N_i is the number of states S_i of observation sequence and, N is the length of the observation sequence.

The comparison is carried out using the test X² (0.05) to judge the 95% significance of the results and then determine if the model is applicable or not. The value of the chi-square X² statistic is computed based on the null hypothesis H ₀ . The method of computing the X² for testing serial independence against Markovian property is extensively discussed in Wilks (2006). In the presented study, the degrees of freedom would be 2 (3 categories -1). At this degree of freedom, the critical value in the test (0.05) is 5.991. The null hypothesis is rejected whenever the computed X² exceeds the critical value (5.991). Otherwise, the model is considered plausible.

Test results have been calculated with (10) and are given in Table 3 with actual probabilities and estimated probabilities of the period 2002/2003:

X ^= 5 i = 1

( PE, - PA ) ²

PE i

Where PE i and PA j are the probabilities estimated by the model and the actual probabilities of the observation series, respectively

In the Table 4, we give the results of test X² (0 05) of periods 2003/2004, 2004/2005 and 2005/2006

Table 3 Estimated probabilities and actual probabilities for 2002/2003

Study area state	Ground		Sea
	PE i	PA i	PE i	PA i
convective	0 1496	0 1432	0 0882	0 0852
Stratiform	0 3434	0 3551	0 2879	0 2942
No-rainning	0 5070	0 5017	0 6239	0 6206
Test: X2 (0.05)	0 0633		0 0753

Table 4 Results of the test X² (0.05) for periods 2003/2004, 2004/2005 and 2005/2006

	Test X2 (0.05)
	Ground	Sea
2003/2004	0 0795	0 0873
2004/2005	0 0813	0 0963
2005/2006	0 0903	0 0996

The values of the test X² (_{0 05}) are lower than 5 991, so they indicate that the prevision probabilities and the actual probabilities are almost identical These results validate the Markov chain model which is used for modeling of precipitation series with three states It is therefore possible to use the matrix of transition probabilities of the Markov chain to predict the evolution of probability distribution over study area

• C.    Discussion

The present study attempts to explain the behavior of precipitation in the Mediterranean region However, the coexistence of convective and stratiform rain complicates their understanding The model takes into account this complexity Indeed, we have used a Markov chain with three states, representing a convective state, a stratiform state and a no raining state The results show that it is the no raining state which tends to be the most persisting Indeed, high probabilities for long sequences are found no rainy However, they are reaching record highs in the sea area The dynamic difference of rainfall between ground and sea has been demonstrated in this study Indeed, the results show that rainy instant tends to favor the rain at the next time in the ground area contrary to the sea area The climate is more unstable in the ground area than in the area sea and the memory effect more pronounced in the sea area compared with ground area This can be explained by the fact that the temperature varies more quickly on ground than on sea The convective precipitation is more frequent in ground than in sea This explained by the effect of orography on precipitation in the ground of the Mediterranean region Stratiform regime appears to be relatively similar in both areas

Moreover, the test result validation shows that rainfall is well described by Markov chains both in ground and in sea

It should be noted that we issued this conclusion after applying the methodology on many areas of radar coverage; the results are identical on the northern part of Algeria and part of the Mediterranean, each of these regions is covered by the radar domain

• V. Conclusion

The main goal of this work was to determine the probability precipitation and to analyze their activities and to discern the difference of its behavior between the ground and the sea. It permits to characterize the variability of the convective-stratiform in the Mediterranean region. The model has been validated by the results of test. All results obtained here are important sources of information for understanding the behavior of precipitation in the region.

The drought trend has been confirmed by this study. This drought is mainly due to global climate change which increased the annual average temperatures. It should be noted that the climate becomes increasingly dry in many countries, including Algeria.

Drought can cause considerable implications and serious consequences for the country's development. Environmental conditions responsible to maintain the ecosystem health of wetlands are degraded because the traditional water management considers only the distribution of water between economic departments and the daily lives of people, ignoring the needs in water for ecosystem functions. The quota of water consumption is unevenly distributed and there is a huge imbalance between offer and demand.

Today, Algeria is more than ever called upon to take measures necessary to address this deficit. The rational use of water resources and the optimal allocation of water resources is necessary to ensure the sustainable development of areas relating to agriculture and the needs of the population.

Moreover, there are watersheds at high altitude (above 1500 m) that receive heavy rainfall. Thus, Algeria has finally important water resources, but they remain poorly exploited.

The authorities concerned must firstly initiate projects for the construction of infrastructure (dams) to hold this water and also expand the measuring device that will allow a better understanding of water resources.

In addition to these factors, the lack of available scientific research has complicated the understanding of water cycle. For these reasons, the plan Orsec has been declared and the rationalization of water distribution has been respected. This work here is part of this logic for the development of methods for assessing water resources and evaluating drought risk in Algeria.

Perspective, further analysis of rainfall in this region deserves to be carried out with dynamic climate models. Indeed, the Markov assumptions used in this article do not represent the all activity rainfall. The rainfall intensity depends on the season and it is linked to the situation day or night. It would be interesting to test this technique over long periods of observation and use of non-homogeneous Markov chains by increasing the order.