Analysis on Shape Image Retrieval Using DNN and ELM Classifiers for MRI Brain Tumor Images
Автор: A. Anbarasa Pandian, R. Balasubramanian
Журнал: International Journal of Information Engineering and Electronic Business(IJIEEB) @ijieeb
Статья в выпуске: 4 vol.8, 2016 года.
Бесплатный доступ
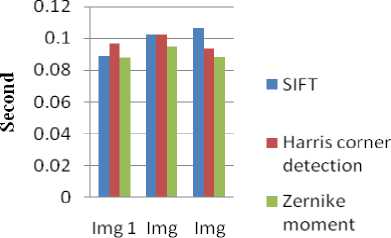
The problem of searching a digital image in a very huge database is called Content Based Image Retrieval (CBIR). Shape is a significant cue for describing objects. In this paper, we have developed a shape feature extraction of MRI brain tumor image retrieval. We used T1 weighted image of MRI brain tumor images. There are two modules: feature extraction process and classification. First, the shape features are extracted using techniques like Scale invariant feature transform (SIFT), Harris corner detection and Zernike Moments. Second, the supervised learning algorithms like Deep neural network (DNN) and Extreme learning machine (ELM) are used to classify the brain tumor images. Experiments are performed using 1000 brain tumor images. In the performance evaluation, sensitivity, specificity, accuracy, error rate and f-measure are five measures are used. The Experiment result shows that highest average accuracy has got at Zernike Moments– 99%. So, Zernike Moments are better than SIFT and Harris corner detection techniques. The average time taken for DNN- 0.0901 sec, ELM- 0.0218 sec. So, ELM classifier is better than DNN. It increases the retrieval time and improves the retrieval accuracy significantly.
Feature extraction, Shape features, Brain Tumor and Classifier
Короткий адрес: https://sciup.org/15013433
IDR: 15013433
Текст научной статьи Analysis on Shape Image Retrieval Using DNN and ELM Classifiers for MRI Brain Tumor Images
Published Online July 2016 in MECS
Now days, a keyword search is not sufficient for the information retrieval techniques. In current trends, Content based image retrieval (CBIR) has very active research area in image processing. CBIR is used to retrieve the digital images from a huge database through browsing and searching. Texture, Color and shape features are the visual content of the image focus on CBIR. Many application areas in CBIR like Military, Medical fields, remote sensing, security and search engines. In the medical field, CBIR focus on visual information for diagnosis and monitoring [1].
The process of creating images of the human body for the purpose of clinical purposes and medical science is called medical imaging. The diagnosis of brain tumor plays an important role in image processing. Magnetic resonance imaging (MRI) is suited for monitoring and evaluating brain tumors. Coronal, sagittal and axial are the three types of image orientation in brain tumors. The coronal is dividing the body into front and back halves. The sagittal is dividing the body into left and right halves and the axial are dividing the body into upper and lower halves. There are modern techniques used in Digital radiography (X-ray), ultrasound, microscopic imaging (MI), Computed Tomography (CT), Magnetic resonance imaging (MRI), Single photon emission computed tomography (SPECT) and Positron emission tomography (PET). MRI is used in the brain for the purpose of bleeding, aneurysms, tumors and damages [9].
The major problem in feature extraction of content based image retrieval with the brain tumor for finding robust shape descriptor image. There are some other problems in shape image retrieval are retrieval time and retrieval accuracy. In this paper, to solve the above the problem through analysis of shape image retrieval for feature extraction method is utilized. The performance analysis of the method has taken for four stages. First stage, preprocessing is utilized to enhance the brain tumor images. Second stage, to extract the shape features of brain tumor images and the methods like Scale Invariant Feature Transform (SIFT), Harris corner detection and Zernike Moments. Third stage, the classification techniques like Deep Neural Network (DNN) and Extreme Learning Machine (ELM) is utilized to classify the brain tumor images. No one insist that which method is best whether analysis of shape image retrieval for brain tumor images. Final stage, to find the similarity matching is used to retrieval of brain tumor images.
This paper organizes as follows: In Section II presents related work, Section III present the methods that have developed to extract brain tumor. Section IV presents
Classification, Section V presents Performance metrics, Section VI presents Experimental results and analysis are given. Finally, the paper is concluded in Section VII.
-
II. Related Work
Demir et al, [3] an automated cancer diagnosis of histopathological images using cell- graph based representation. The edges of a cell-graph is performed as tissue level diagnosis of brain cancer called malignant glioma. The brain biopsy samples 646 images and 60 different patients are tested in at least 99% accuracy for healthy tissues with lower cellular density level and at least 92% accuracy for benign tissues with similar high density level. Othman et al, [8] has developed to find a normal patient and abnormal tumor patient of MRI data using Support vector machine (SVM) classifier is performed. The discrete wavelet transform is used to extract the features of MRI brain image. The disadvantage is SVM actually cannot work accurately with a large data. The training complexity of SVM is highly dependent on the size of data.
Ahmed et al, [6] an efficacy of different types of features such as texture, shape and intensity for segmentation of Posterior- Fossa tumor. The four different techniques like PCA, boosting, KLD and entropy metrics demonstrate the efficacy of 249 real MRI of ten pediatric patients. Chaovalitwongse et al, [10] have developed to improve the pattern and network based classification techniques for multichannel medical data. Support feature machine (SFM) and neutral based support vector machine (NSVM) are the two classification techniques are performed for diagnosis and treatment of human epilepsy in EEG data. Yang et al, [7] have a generalized brain state in a box (gBSB) based hybrid neural network. Using Hybrid neural network can store and retrieve large-scale patterns combining the pattern decomposition concept and pattern sequence storage and retrieval.
Azhari et al, [14] automatic brain tumor detection and localization frameworks are utilized in the purpose of detection and localize brain tumor in magnetic resonance imaging. It can demonstrate that a simple machine learning classifier gives in higher classification accuracy. Esther et al, [16] to retrieve brain image using soft computing technique. The shape features are extracted using 2-D Zernike moments. The soft computing technique of Extreme Learning Machine is used with different distance metric measures like Euclidean, Quasi Euclidean, City Block, Hamming distance. The Fuzzy Expectation Maximization Algorithm is used to remove the non-brain portion of the MRI Brain image.
Rajalakshmi et al, [15] a relevance feedback method using a diverse density algorithm is used to improve the performance of content- based medical image Retrieval. The texture features are extracted based on Haralick features, Zernike moments, histogram intensity features and run -length features. The hybrid approach of branch and bound algorithm and artificial bee colony algorithm using brain tumor images. The classification is performed using Fuzzy based Relevance Vector Machine (FRVM) to form groups of relevant image features.
-
III. Feature Extraction
When the input data to an algorithm is too large to be processed and it is suspected to be redundant. So transforming the input data into the set of features is called feature extraction [20].
-
A. Shape
Shape is an important role to identify the human recognition and perception. To identify the object, Shape feature provides a powerful cue for human perception and segment the image into regions or objects. The major issues in content based image retrieval for finding robust shape descriptor image. In the medical field, shape is used to describe the similarity of medical scans. The main objective of the shape is used to classify the deformations from pathological changes in dental radiographs and retrieving tumors. In CT scan, detecting emphysema in high resolution of the lung images for shape content [2].
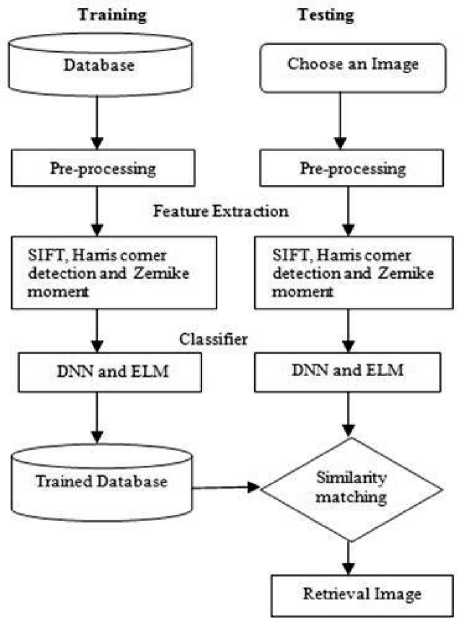
Fig.1. Flowchart of Shape image retrieval
-
B. Preprocessing
The first step of the image retrieval process is preprocessing to capture the MRI brain tumor image and convert RGB to Gray. To resize the image in the database as 256 x 256. The Preprocessing step is used to enhance the visual appearance of an image using contrast enhancement techniques. The Contrast enhancement is used to perform adjustments on the darkness or lightness of the image.
-
C. Feature Extraction Techniques
Shape features are extracted using feature extraction techniques like Scale invariant feature transform, Harris corner detection and Zernike moments.
-
D. Scale Invariant Feature Transform
The Scale-Invariant Feature Transform (or SIFT) is an algorithm in computer vision to detect and describe local features in images. The key point detector and key point descriptor are the two components of the SIFT. First, the key point detector is used to detect key points in an image which are invariant for transformation. Second, the key point descriptor is used to describe the appearance of the surrounding region of that key point. SIFT has the potential for finding a large number of local features [17],[21].
-
1) SIFT Algorithm
-
a) Scale-space extrema detection
For scale space extrema detection in the image is first convolved with Gaussian-blurs at different scales. Finding key points as maxima/minima of the Difference of Gaussian (DoG) that occur multiscales.
DoG image D ( x , y , a ) is given by
D ( x , y , a ) = L ( x , y , k a ) - L ( x , y , kja ) (1)
Where L ( x , y , k a ) is the convolution of the original image I ( x , y ) Gaussian G ( x , y , k a ) L ( x , y , k a ) at scale k
L ( x , y , k a ) = G ( x , y , k a ) * I ( x , y ) (2)
k ta and kj a gaussian blured imagescales
-
b) Keypoint localization is used to perform a detailed fit to the nearby data for accurate location, scale, and ratio of principal curvatures.
-
i) Interpolation of nearby data for accurate position
aD 1
D (x) = D +--x +--F —x x(3)
ax 2xTa
D is the derivatives, x = ( x , y , a )
-
ii) Discarding low contrast key points
-
iii) Eliminating edge response
-
c) Orientation Assignment
Each keypoint is assigned one or more orientations based on local image gradient directions. This is the key step in achieving invariance to rotation as the keypoint descriptor can be represented
-
d) Keypoint descriptor
To compute a descriptor vector for each keypoint such that the descriptor is highly distinctive and partially invariant to the remaining variations such as illumination, 3D viewpoint, etc.
-
E. Harris Corner Detection
The Harris corner detector is mainly used in the methods of corner detection. The Harris corner detector is used to detect the corner features that contain high intensity changes in both the horizontal and vertical directions. It is an established technique using linear filtering of an image [19],[22],[23].
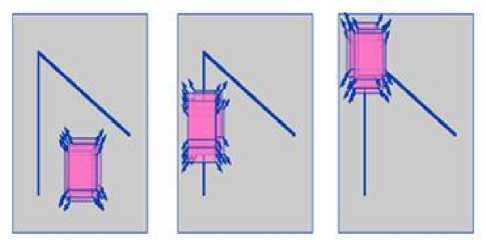
a) Flat region b) edge region c) corner region
Fig.2.
-
1) Harris Corner detection algorithm
-
1) The weighted sum of squared differences (SSD) between two patches denoted S is given by
S ' ( x , y ) = Z u z . w ( u , v ) ( I ( u + x , v + y ) - 1 ( u , v ))2
l et i be the image, ( u , v ) an image patch over the area and shifting it by (x,y)
I ( u + x , v + y ) can be Taylor expansion
-
2) Calculate the derivative of the image
I ( u + x , v + y ) « I x ( u , v ) x + I y ( u , v ) y (5)
Let I and I be the partial derivatives of I
-
3) For each pixel(x,y) can be written in the matrix form
S ( x , y ) « ( x , y ) A

A = T u T v w ( u , V )
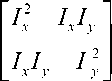
A is the structure sensor
-
4) Calculate the response of the detector
Mc = ЛЛ - k Ц + Л ) 2 = det( A) - k trace 2 ( A )
M is the computation of square root and k is a tunable parameter.
-
F. Zernike Moments
Zernike Moments, a type of moment function, are the mapping of an image onto a set of complex Zernike polynomials. Zernike polynomials are orthogonal to each other; Zernike moments can represent the properties of an image with no redundancy or overlap of information between the moments. Due to these characteristics, Zernike Moments have been utilized as feature sets in content-based image retrieval [4].
-
1) Zernike Moments Algorithm
-
1) Choose the parameter 9 , n and m.
9 is a rotation angle, n is a order and m is a continuous function f ( x , y )
-
2) Calculate the radial polynomial from the given equation
V_ ( P . 9 ) = R . ( p ) J (7)
Where R ( 9 ) is real values radial polynomial
-
3) Compute the Zernike basis function from the radial polynomials
0< p <1
J J V‘* m ( *' ( P , 9 ) PdPd9 = —AnAm
J 0 <9< 2 n n + 1
Where * denotes the complex conjugate and
-
4) Compute the Zernike moments by projecting the image on to the basic functions
Anm = n + 1 T x T y f ( x , У) V*m ( x , У ), x2 + У 2 < 1 (9)
A denotes Zernike moment nm
X 2 + y 2 < 1, 0 < m < n , V m ( X , y ) is even, used to describe the intensity of normalized image.
-
IV. Classification
Classification is the process in which ideas and objects are recognized, differentiated, and understood. The Deep neural network (DNN) and Extreme learning machine (ELM) are the classification techniques used for MRI brain tumor images.
-
A. Deep Neural Network
Deep neural network (DNN) is a multilayer neural network model that has more than one layer of hidden units between its inputs and its outputs. The two important processes are used in the classification are training and testing phase. In the training phase, the features of training data are trained using deep learning classifier. Artificial Neural Networks provide a powerful tool to analyze, model and predict. The benefit is that neural networks are data driven, self adaptive methods. Commonly used neural network uses back propagation algorithm. But it is not adequate for training neural networks with many hidden layers on large amounts of data. Deep Neural Networks that contain many layers of nonlinear hidden units and a very large output layer. Deep neural networks have deep architectures which have the capacity to learn more complex models than shallow ones [5],[12],[18].
Each hidden unit, j and uses the logistic function to map its total input from the layer below, x to the scalar state, y sends to the layer y = log istic(X ) = —1-7-, 1 + e j
Xi = bi +V yWn j j i i ij
Where bj is the bias of unit j, I is an index over units in the layer, and wij is a the weight on a unit j from the unit I in the layer. For multiclass classification, the output unit j converts its total input, xj, into a class probability, pj, using the softmax non linearity exp(xj)
pi = V T k e xp ( x k )
Where k is an index over all classes
C = -Tj d J log Pj(12)
C is the cost function, cross entropy between the target probabilities d and the output of the softmax p [18].
К P X X Pd C
Awj (t) = Awij(t -1)- e -—— a wij(t)
Fig.3. Examples of functions represented by a graph of computations
x. g Rd and y. g Rd . Then a SLFN with M hidden neutrons is modeled as the following sum
ZMi px(wx+bi) jG [1, N] (14)
With f being the activation function w the input weights to the ith neuron in the hidden layer, b the hidden layer biases and the output weights.
In the case where в the SLFN would perfectly approximate the data (meaning the error between the output y and the actual value y is zero), the relation is
ZM1 px(w.xj+b)=yj, jg[1,N] (15)
1) DNN Algorithm
-
1) In the first phase, greedily train subsets of the parameters of the network using a layerwise and supervised learning criterion, by repeating the following steps for each layer (i G {1,...,1})
Until a stopping criteria is met, iterate through training database by
-
(a) mapping input training sample x t to representation h 1 ( Xt ) (if i > 1) and hidden representation h i ( xt ) .
-
(b) updating parameters b - 1 , b i and Wl of layer i using some supervised learning algorithm.
Also, initialize (e.g., randomly) the output layer parameters b + 1, Wl + 1 .
-
2) In the second and final phase, fine-tune all the parameters of the network using backpropagation and gradient descent on a global supervised cost function C ( Xt , yt , 5 ) with input xt and label yt , that is, trying to
make steps in the direction E
d C ( xt , yt , 5 ) d 5
-
B. Extreme learning machine
The Extreme learning machine (ELM) is single layer feedforward neural network (SLFNs) which chooses randomly hidden nodes and the output weights of SLFNs. The randomly chooses of input weight and hidden biases of SLFNs can be assigned if the activation functions in the hidden layer are infinitely differentiable. The output weight (linking the hidden layer to the output layer) of SLFNs can be inverse operation of the hidden layer output matrices. The learning speed of the extreme learning machine is a thousand times faster than feed forward network algorithm like back propagation (BP) algorithm. The learning algorithm tends to reach the smallest training error, good performance, obtains the smallest norm of weights and runs extremely fast SLFN learning algorithm can be easily implemented is called an extreme learning algorithm[11].
Consider set of N distinct samples ( x , y ) with
Which can be written compactly as H P = Y
Where H is the hidden layer output matrix defined as
(f (WX + b) and P = (А,".’ Pm )T
Where H is the hidden layer output matrix defined as f ( w1.x1 + b) •• • f ( wm,. x1 + bm )
H =
.f ( w 1 . x 1 + b) •• • f ( w m, . x n + Ьт )
-
1) ELM Algorithm
Given a training set ( x , y .), x G R d , y G Rd an activation function f : R ^ R and M hidden nodes
-
1. Randomly assign input weights w and biases b , .
-
2. Calculate the hidden layer output matrix H
-
3. Calculate output weights matrix P = H T Y
i g[1, M ]
-
V. Performance Metrics
Sensitivity, specificity, accuracy, error rate and f-measure are used to measure the performance of SIFT, Harris corner detection and Zernike moments.
-
A. Sensitivity
Specificity measures the proportion of positives which are correctly identified, such as the percentage of sick people who are correctly identified as not having the condition, sometimes called the true negative rate [13].
Sensitivity = -- ——X 100 (17)
TP + FN
Where, TP – True Positive (equivalent with hit)
FN – False Negative (equivalent with miss)
TN – True Negative (equivalent with correct rejection)
-
B. Specificity
Specificity measures the proportion of negatives which are correctly identified, such as the percentage of healthy people who are correctly identified as not having the condition, sometimes called the true negative rate [13].
TN
Specificity = -------- X 100 (18)
FP + TN
Where, TN – True Negative (equivalent with correct rejection)
FN – False Negative (equivalent with miss)
TN – True Negative (equivalent with correct rejection)
-
C. Accuracy
Accuracy is the measurement system, which measure the degree of closeness of measurement between the original value and the extracted value [13].
Accuracy =
TP + TN
TP + FP + TN + FN
X 100
Tamil Nadu, India. The dataset is in the type of Digital Imaging Communication Medicine (DICOM) brain tumor images. It contains 5 classes and each class has 200 images. The resolution of the image is 256 x 256. For quantitative analysis, the Sensitivity, Specificity, Accuracy, Error rate and F-measure parameters are evaluated.
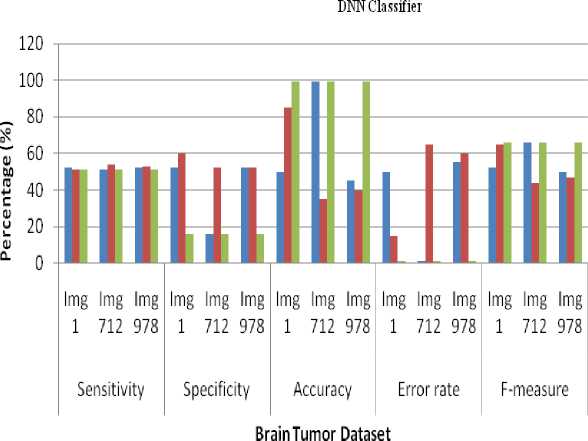
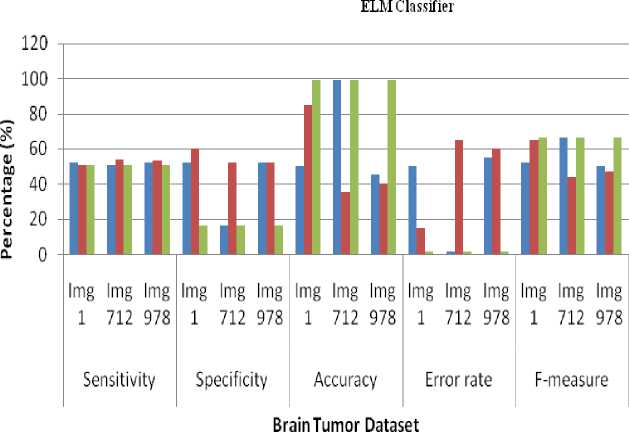
The Experimental results shows that the average sensitivity for DNN and ELM classifier in SIFT- 51.66%, Harris corner detection- 52.66%, Zernike Moments- 51%. The performance of the average specificity of DNN and ELM classifier in SIFT- 40%, Harris corner detection-54.66%, Zernike Moments- 16%. The performance of the average Accuracy of DNN and ELM classifier in SIFT-64.66%, Harris corner detection- 53.33%, Zernike Moments- 99%. The performance of the average error rate of DNN and ELM classifier in SIFT- 1%, Harris corner detection- 1%, Zernike Moments- 1%. The performance of the average Accuracy of DNN and ELM classifier in SIFT- 56%, Harris corner detection- 52%, Zernike Moments- 66%. The Experiment result shows that highest average accuracy has got at Zernike Moments– 99%. So, Zernike Moments are better than SIFT and Harris corner detection techniques. The average time taken for DNN- 0.0901 sec, ELM- 0.0218 sec. So, ELM classifier is better than DNN.
Where, TP – True Positive (equivalent with hit)
FN – False Negative (equivalent with miss)
TN – True Negative (equivalent with correct rejection)
-
D. Error rate
Error rate is used to compare an estimate value to an exact value [13].
Error rate = 100 - Accuracy (20)
-
E. F-measure
F -measure is a harmonic mean of precision and recall [13].
F - measure =-------- X 100 (21)
2 TP + FP + FN
TP- number of true positive
FP- number of false positive
FN- number of false negative
Fig.4. Sample images
-
VI. Experimental Results and Analysis
To evaluate the overall performance of the brain tumor image are the type of both sagittal and axial. The MRI brain tumor image database contains 1000 images. The original dataset has taken from Aarthi scans, Tirunelveli,
Fig.5. Retrieval of brain tumor images
Table 1. Computing of sensitivity, specificity, accuracy, error rate and f-measure for SIFT, Harris corner detection and Zernike Moments using DNN classifier
|
DNN Classifier |
Sensitivity |
Specificity |
Accuracy |
Error rate |
F-measure |
||||||||||
|
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
|
|
SIFT |
52 |
51 |
52 |
52 |
16 |
52 |
50 |
99 |
45 |
50 |
1 |
55 |
52 |
66 |
50 |
|
Harris Corner Detection |
51 |
54 |
53 |
60 |
52 |
52 |
85 |
35 |
40 |
15 |
65 |
60 |
65 |
44 |
47 |
|
Zernike Moments |
51 |
51 |
51 |
16 |
16 |
16 |
99 |
99 |
99 |
1 |
1 |
1 |
66 |
66 |
66 |
-
■ SIFT
-
■ Harris corner detectionZernike Moments
Fig.6. Retrieval performance of sensitivity, specificity, accuracy, error rate and f-measure for SIFT, Harris corner detection and Zernike Moments using DNN classifier
Table 2. Computing of sensitivity, specificity, accuracy, error rate and f-measure for SIFT, Harris corner detection and Zernike Moments using ELM classifier
|
ELM Classifier |
Sensitivity |
Specificity |
Accuracy |
Error rate |
F-measure |
||||||||||
|
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
Img 1 |
Img 712 |
Img 978 |
|
|
SIFT |
52 |
51 |
52 |
52 |
16 |
52 |
50 |
99 |
45 |
50 |
1 |
55 |
52 |
66 |
50 |
|
Harris Corner Detection |
51 |
54 |
53 |
60 |
52 |
52 |
85 |
35 |
40 |
15 |
65 |
60 |
65 |
44 |
47 |
|
Zernike Moments |
51 |
51 |
51 |
16 |
16 |
16 |
99 |
99 |
99 |
1 |
1 |
1 |
66 |
66 |
66 |
-
■ SIFT
-
■ Harris corner detectionZcrnikc Moments
-
Fig.7. Retrieval performance of sensitivity, specificity, accuracy, error rate and f-measure for SIFT, Harris corner detection and Zernike Moments using DNN classifier
Table 3. Computing Total time taken for DNN classifier in SIFT, Harris corner detection and Zernike Moments
|
Total time (sec) |
Img 1 |
Img 712 |
Img 978 |
|
SIFT |
0.0889 |
0.1026 |
0.1067 |
|
Harris corner detection |
0.0966 |
0.1027 |
0.0939 |
|
Zernike moments |
0.0876 |
0.0946 |
0.0881 |
Table 4. Computing Total time taken for ELM classifier in SIFT, Harris corner detection and Zernike Moments
|
Total time (sec) |
Img 1 |
Img 712 |
Img 978 |
|
SIFT |
0.0104 |
0.0101 |
0.0103 |
|
Harris corner detection |
0.0147 |
0.0188 |
0.0094 |
|
Zernike moments |
0.0216 |
0.0226 |
0.0214 |
Total Time Taken for DNN
712 978
Bi ain Tumor Dataset
-
Fig.8. Retrieval performance of Total time taken for DNN classifier in SIFT, Harris corner detection and Zernike Moments
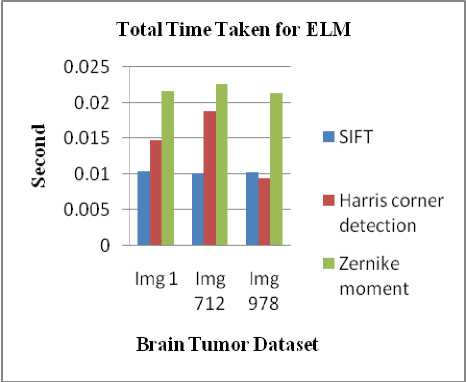
Fig.9. Retrieval performance of Total time taken for ELM classifer in SIFT, Harris corner detection and Zernike Moments
-
VII. Conclusion
In this paper, the performance of shape feature extraction for MRI brain tumor image retrieval is evaluated. The Scale Invariant Feature Transform (SIFT), Harris corner detection and Zernike moments are the techniques used for shape feature extraction. To classify, the brain tumor image for supervised learning algorithms like DNN and ELM is used. For DNN and ELM classifier, Comparing the Sensitivity, Specificity values for Harris corner detection is better than the SIFT, Zernike Moments.
It is inferred from the results that Zernike moments using DNN and ELM classifier outperform other techniques like SIFT and Harris corner detection. When compared against time, ELM classifier outperforms DNN. So, Zernike Moments achieves better performance and ELM classifier achieves better performance.
Список литературы Analysis on Shape Image Retrieval Using DNN and ELM Classifiers for MRI Brain Tumor Images
- Rui, Yong, Thomas S. Huang, and Shih-Fu Chang. "Image retrieval: Current techniques, promising directions, and open issues." Journal of visual communication and image representation 10.1: 39-62, March 1999.
- Castelli, Vittorio, and Lawrence D. Bergman, Eds. Image databases: search and retrieval of digital imagery. John Wiley & Sons, 2004.
- Demir, Cigdem, S. Humayun Gultekin, and Bulent Yener. "Learning the topological properties of brain tumors." IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB) 2.3: 262-270, September 2005.
- Li, Shan, Moon-Chuen Lee, and Chi-Man Pun. "Complex Zernike moments features for shape-based image retrieval." Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on Vol. 39, No. 1, January 2009R. Nicole, "Title of paper with only first word capitalized", J. Name Stand. Abbrev., in press.
- Larochelle, Hugo, Yoshua Bengio, Jérôme Louradour, and Pascal Lamblin. "Exploring strategies for training deep neural networks." The Journal of Machine Learning Research 10: 1-40, September 2009.
- Yang, Liu, Rong Jin, Lily Mummert, Rahul Sukthankar, Adam Goode, Bin Zheng, Steven CH Hoi, and Mahadev Satyanarayanan. "A boosting framework for visuality preserving distance metric learning and its application to medical image retrieval." Pattern Analysis and Machine Intelligence, IEEE Transactions on 32, no. 1: 30-44, January 2010.
- Ahmed, Shaheen, Khan M. Iftekharuddin, and Arastoo Vossough. "Efficacy of texture, shape, and intensity feature fusion for posterior-fossa tumor segmentation in MRI." Information Technology in Biomedicine, IEEE Transactions on 15.2: 206-213, March 2011.
- Othman, Mohd Fauzi Bin, Noramalina Bt Abdullah, and Nurul Fazrena Bt Kamal. "MRI brain classification using support vector machine." Modeling, Simulation and Applied Optimization (ICMSAO), 4th International Conference on. IEEE, April 2011.
- Somasundaram. K., and T. Kalaiselvi. "Automatic brain extraction methods for T1 magnetic resonance images using region labeling and morphological operations." Computers in Biology and Medicine 41.8: 716-725. August 2011
- Chaovalitwongse, Wanpracha Art, Rebecca S. Pottenger, Shouyi Wang, Ya-Ju Fan, and Leon D. Iasemidis. "Pattern-and network-based classification techniques for multichannel medical data signals to improve brain diagnosis." Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on 41, no. 5: 977-988, August 2011.
- Huang, Guang-Bin, Hongming Zhou, Xiaojian Ding, and Rui Zhang. "Extreme learning machine for regression and multiclass classification." Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on 42, no. 2 : 513-529. January 2012.
- Hinton, Geoffrey, Li Deng, Dong Yu, George E. Dahl, Abdel-rahman Mohamed, Navdeep Jaitly, Andrew Senior et al. "Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups." Signal Processing Magazine, IEEE 29, no. 6: 82-97, November 2012.
- Ahirwar, Anamika. "Study of Techniques used for Medical Image Segmentation and Computation of Statistical Test for Region Classification of Brain MRI." International Journal of Information Technology and Computer Science (IJITCS) 5.5 (2013): 44
- Azhari, Ed-Edily Mohd, et al. "Brain tumor detection and localization in magnetic resonance imaging." International Journal of Information Technology Convergence and services (IJITCS) 4.1 (2014): 2231-1939.
- Rajalakshmi, T., and R. I. Minu. "Improving relevance feedback for content based medical image retrieval." Information Communication and Embedded Systems (ICICES), 2014 International Conference on. IEEE, February 2014.
- Esther, J., and M. Mohamed Sathik. "Retrieval of Brain Image Using Soft Computing Technique." Intelligent Computing Applications (ICICA), 2014 International Conference on. IEEE, March 2014.
- Bandaru, Rajanna, and Dinesh Naik. "Retrieve the similar matching images using reduced SIFT with CED algorithm." Control, Instrumentation, Communication and Computational Technologies (ICCICCT), 2014 International Conference on. IEEE, July 2014.
- Gladis Pushpa V.P, Rathi and Palani .S, "Brain Tumor Detection and Classification Using Deep Learning Classifier on MRI Images" Research Journal of Applied Sciences Engineering and Technology10(2): 177-187, May-2015, ISSN:20407459;
- Woo, Jonghye, Maureen Stone, and Jerry L. Prince. "Multimodal Registration via Mutual Information Incorporating Geometric and Spatial Context." Image Processing, IEEE Transactions on 24.2: 757-769. January 2015.
- https://en.wikipedia.org/wiki/Feature_extraction
- https://en.wikipedia.org/wiki/SIFT
- http://www.cse.psu.edu/~rtc12/CSE486/lecture06.pdf
- https://en.wikipedia.org/wiki/Corner_detection


