Анастомоз в квазиклеточных сетях

В работах автора [1,  2 и др.] приводятся различные подходы к синтезу квазиклеточных сетей. Наряду с методом базового графа, описанного в [1], существуют различные методы, позволяющие синтезировать дискретные структуры (рис. 1), представляющие собой множества, каждый элемент которых имеет вид:

Qi=( x ci, У ci ,Si)                                              (1)

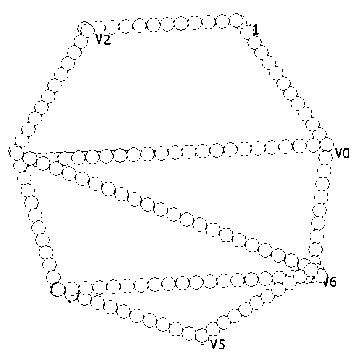
Рис. 1. Квазиклеточная сеть

Динамические аспекты квазиклеточных сетей описаны в работах [1, 2]. Особое внимание при формировании структуры квазиклеточной сети следует уделить вопросам вычисления координат x ci , ^yci при синтезе. Одним из подходов к вычислению координат является моделирование поведения микрообъекта — генерирующей фишки, формирующей клетку в каждый момент времени. Тогда для соседних клеток, синтезируемых поочерёдно справедливо:

xa+ 1= xa+ A xa ,(2)

У ci +1= Ус+ А Уа

Учитывая условие соседства клеток, определённое в [1]:

(xc+ 1- xci)2+ (yc+ 1- yd )2< 4R2 ,(4)

справедливо, что смещение координат микрообъекта при синтезе не должно превышать 2R, т.е.:

А2 Х ci + А2 Усг< 4R2 .(5)

При обращении условия (5) в равенство, клетки сформированной квазиклеточной сети не пересекаются. Таким образом, синтез квазиклеточной сети методом генерирующей фишки позволяет решить проблему пересечения клеток. Однако, нетрудно привести ситуацию, при которой генерирующая фишка попадает в тупик, поскольку дальнейшее её движение приводит к появлению самопересечений:

V j : Ч ( x ci ^{- x}j ^{) 2} + ⁽ y ci ^- Уз ^{) 2} = 4R² .                                ⁽⁶⁾

Типичный пример такой ситуации приведён на рис. 2. Чёрным отмечено начальное положение генерирующей фишки. Такая ситуация называется тупиком генерирующей фишки. При этом не существует Δ x ci , Δ y ci при которых на очередной итерации выполнения (2), (3) не нарушается условие (6). Подобная ситуация часто возникает при случайном задании величин A x ci , A ^yct .

Рассмотрим способы решения проблем тупиков, а также синтеза пересечений в квазиклеточных сетях. Стоит обратить внимание на достаточно частые ситуации, возникающие при синтезе квазиклеточных сетей методом базового графа [1]. Следует отметить, что фактически метод базового графа позволяет синтезировать динамическую дискретную структуру на базе статической. По сути статическая структура приобретала возможность рассмотрения её динамических аспектов. Уже на раннем этапе изучения квазиклеточных сетей прослеживается их связь с теорией потоков в сетях, описанной в работах [3, 4]. Следует обратить внимание на следующий пример (рис. 3). Здесь можно наблюдать несколько клеток, выделенных цветом, и нарушающих связь со структурой базового графа.

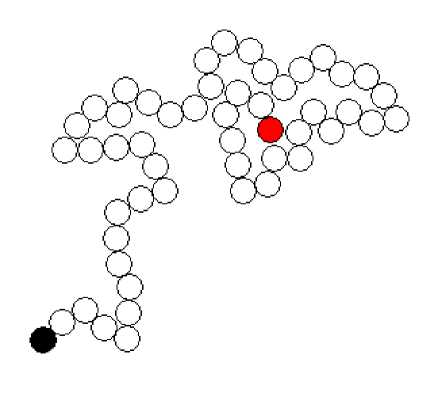
Рис. 2. Тупик генерирующей фишки

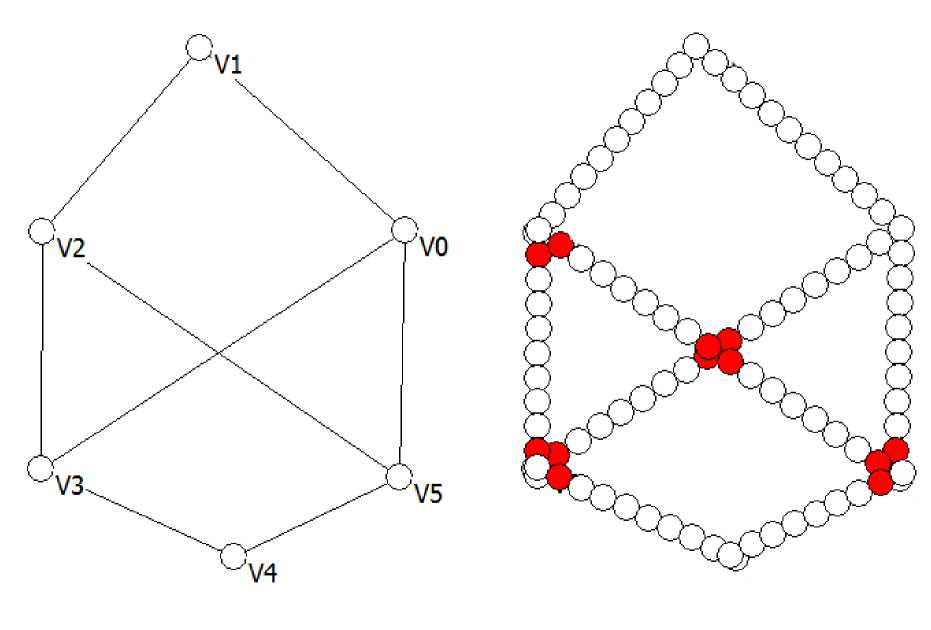
Рис. 3. Нарушение связи со структурой базового графа

Действительно, обозначенные клетки фактически получены путём деления различных рёбер, но при этом рассматриваемые клетки являются соседними, т.е. для них выполняется:

( xu- xv )2+ ( Уи- yv )2 ^ ( 2 R )2 .

Также особое внимание следует уделить рёбрам, пересекающимся не в вершинах. Учитывая специфику генерации квазиклеточной сети на основе базового графа, на таких рёбрах очевидно наличие клеток, являющихся соседними. В описанной ситуации циркуляция может не соответствовать смежности в базовом графе [1, 3], что приводит к неадекватному преобразованию моделей, в частности модели потоков в сетях в квазиклеточные сети. Фактически, предполагается проникновение фишек при циркуляции в клетки, между которыми не должно быть соседства. Такую ситуацию можно сравнить с медицинским явлением, называемым анастомозом, т.е. естественным или искусственным соустьем органов, имеющих полость [5]. Назовём подобное явление в квазиклеточных сетях также анастомозом по аналогии с медицинским термином. Рассматривая понятие анастомоза в квазиклеточных сетях, следует учитывать, что при генерации методом базового графа клетка образуется на основе деления ребра графа, а в методе генерирующей фишки на основе сдвига микрообъекта от некоторого расположения, в котором ранее построена клетка. В такой ситуации рёбра базовых графов, а также клетку, сформированную на предыдущей итерации, при синтезе методом генерирующей фишки, считаем базовыми объектами для сформированных на их основе клеток квазиклеточных сетей. Обозначим ребро

⁽ V ia , V ib ) базового графа. Тогда

считаем, что для каждой клетки

^Qp  ⁽ x p^,yp^,Sp ) , для

которой:

xp = xia + p dx ' Ур = Уа + p dy'

xib где dx

-

n

x ia. , dy' = y b - y a. , ребро ( V ia , V ib ) является базовым. Обозначим

отношение между клеткой Q p и ребром ⁽ V ia , V ib ) как

Q p е ( Via , V ib ) .

Для генерации клеток методом генерирующей    фишки клетка

Qi = (x ci, yi , Si) является базовой для Qi + 1= (x ci + 1 , yci + 1, Si +1) при xci+ 1

= x ci ⁺ A x ci

У сг + 1 = y ^{+ A} У сг .

Тогда введём определение. Анастомозом в квазиклеточной сети называется пересечение клеток, относящихся к различным базовым элементам. Рёберным анастомозом будем считать пересечение клеток, относящихся к разным рёбрам базового графа G = < V,U ) , т.е.

I Q u =( X u ,y u ,S u )

Q v =( X v ,y v ,S v )

Q u ∈ U i ;Q v ∈ U j ;U i ≠ U j x u - ^xv ^{) 2 +(} У и - y v⁾² ^ ⁽ 2 R ⁾²

Анастомозом генерирующей фишки называется ситуация, при которой генерирующая фишка, находящаяся на i -й итерации формирования квазиклеточной сети в координатах ⁽ x ci , ^y ci ) , нарушает условие:

V j : ^ ( x ci - x j ) 2 ^{+ (} У_d - y j ^{) 2} ^ 4R 2 .                              ⁽¹⁴⁾

Таким образом, при синтезе квазиклеточных сетей достаточно часто возникает анастомоз, нарушающий преобразование дискретных структур в методе базового графа. В условиях тупика генерирующей фишки анастомоз позволяет решить проблему и продолжить генерацию. Следует отметить, что в зависимости от условий задачи и предметной интерпретации, анастомоз можно считать допустимым. Несмотря на это, особое внимание следует уделить подходам к синтезу квазиклеточных сетей с учётом анастомоза без нарушения адекватности преобразования моделей базового графа, а также предотвращения тупика генерирующей фишки.